基于小波变换的ICESAT-GlAS波形处理
2012-08-02邢艳秋李立存
邱 赛,邢艳秋,李立存,王 萌
(东北林业大学森林作业环境研究中心,哈尔滨150040)
搭载在冰、云和陆地高程卫星 (the ice,cloud,and land elevation satellite,ICESat)上的地学激光测高系统 (geoscience laser altimeter system,GLAS)获取的原始波形数据由于受系统噪声和大气的影响存在着较大的白噪声,另外ICESATGLAS在以植被分布为主要特征的激光脚点中不仅包含植被信息,还包括地形陡变处、枯落木、石块等地物信息,造成其波形数据失真、叠加[1],因此需要对其进行降噪处理。小波变换1是一种时间窗和频率窗都改变的时频局域化分析法,既具备短时傅里叶变换局部化的思想,又克服了窗口大小不随频率变化的缺点,具有自适应性[2-5],因此小波变换在信号去噪中具有很好的应用前景。用小波变换法的去噪效果在很大程度上取决于小波基,因为并不是所有的小波基都适合于激光雷达数据信号的处理,即使是同一信号用不同的小波基进行处理也会产生不同的结果。小波基的选择目前没有统一的标准,本文是通过比较分析小波基的5个主要参数(正交性、对称性、正则性、消失矩、支撑长度)来确定选用哪种小波基,并以吉林省汪清林业局经营区的ICESAT-GLAS波形数据为研究对象,进行去噪效果的比较分析。
1 数据收集及其预处理
1.1 ICESAT-GLAS 数据
本文采用的ICESAT-GLAS数据是从美国国家冰雪数据中心 (NSIDC)(http://nsidc.org/data/icesat)下载的。ICESAT-GLAS数据产品可分为3个级别:0、1和2级,共15种产品,本文采用的是1A级数据中的GLA01和GLA14两种数据产品。其中GLA01中包括光斑号、光斑帧号、时间、脉冲强度 (光电压值)、经纬度等信息,GLA14记录了地表的高度信息,包括高程、大地经纬度、回波振幅、面积和标准差。本次研究利用的数据坐标是WGS84坐标。
1.2 波形数据预处理
(1)ICESAT-GLAS原始波形数据的数据格式为整数型二进制格式,在MATLAB和IDL平台上将其转化为十进制的ASCII(American Standard Code for Information Interchange,ASCII)格式 (*.rasc)[6]。
(2)根据激光光斑脚点的经纬度坐标将GLA01数据与GLA14的相关波形信息合成,包括光电压值、高程、接收与发送的UTC时间等波形信息与参数。
(3)将数据分别保存到文本文档中,再加载到MATLAB文件中,并转存为为.mat文件的格式,然后对其进行去噪处理。
2 波形数据去噪
2.1 小波变换原理

小波,是一种小区域的波,小波变换的实质是将L2(R)空间中的任意函数f(t)表示成为其在小波核函数Ψa,b(t)之上的投影的叠加,即小波变换是信号f(t)和Ψa,b(t)的内积,公式为:
公式 (1)中a,b,t均为连续变量。
Ψa,b(t)是由给定的小波基Ψ (t)在伸缩因子a和平移因子b下进行伸缩和平移得到函数族:
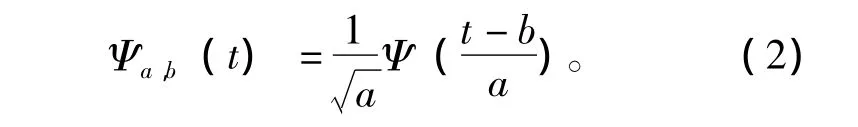
ab∈R;a〉0 其中a为伸缩因子,b为平移因子。
2.2 小波基的的选择
小波变换中采用的小波基函数Ψ(t)具有多样性,因此用不同的小波基函数分析同一问题会有不同的结果。本文通过对小波基的主要参数[7](正交性、对称性、正则性、消失矩、支撑长度)进行比较分析初步判定两种小波基 (Daubechies、Symlets)对波形数据进行处理是较好的。本文选取的是db1小波基和sym7小波基进行比较。表1为常用小波基所对应重要参数特点。
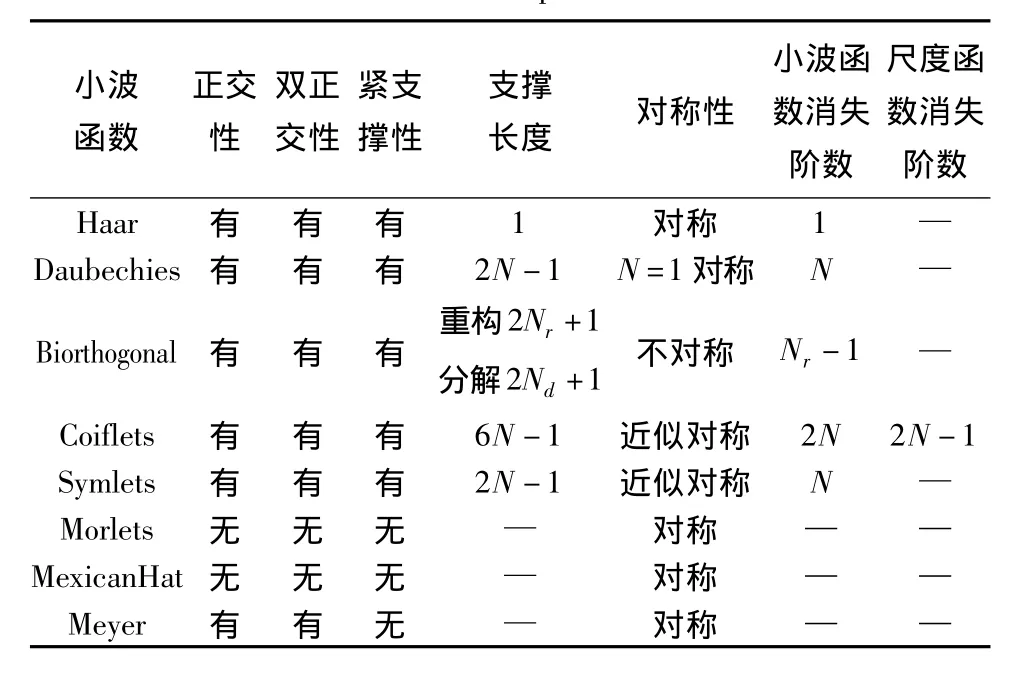
表1 常用小波参数特性Tab.1 Common wavelet basis parameters'characteristics

2.3 小波去噪过程
本文假设激光雷达波形信号f(t)为离散采样后的得到的544点的离散信号f(n),n=1,2,……544。对信号去噪的具体过程如下:
(1)一维小波分解
本文选择分解为4层,将信号分解成不同频率通道成分,并将每个频率通道成分按相位进行了分解,获取小波分解高频系数WΨf(a,b),如公式(3)所示:
{aN-2k}和 {bN-2k}是分解序列,N为采样点数,j表示分解的层数,Cj=
(2)对小波高频系数进行阈值化处理
D.L.Dohono提出阈值化处理方法包括硬阈值法和软阈值法,一般,硬阈值比软阈值处理后的信号粗糙,所以本文采用软阈值法处理。具体公式如 (4)所示:

Wδ为量化后的小波系数值,w为分解后的小波系数,sgn(·)是符号函数
用阈值法去噪最关键的是确定阈值δ,本文采用的是Birge-Massart惩罚函数方法来由小波系数选择规则得到[8]。
(3)一维小波重构
根据小波分解后的最底层低频系数和各层经过阈值量化处理后的高频系数进行一维小波重构。具体如公式 (5)所示:

{pk-2N}和 {qk-2N}是重建序列,N为采样点数,j表示分解的层数,Cj=Cjk。
3 去噪效果评价
本文采用信噪比 (SNR)和均方根误差(RMSE)做为评价指标,对同一波形数据去噪效果进行评价[9]。具体如公式 (6)、 (7)所示:s(i)为含噪信号,f(i)为去噪后信号,L为信号长度。
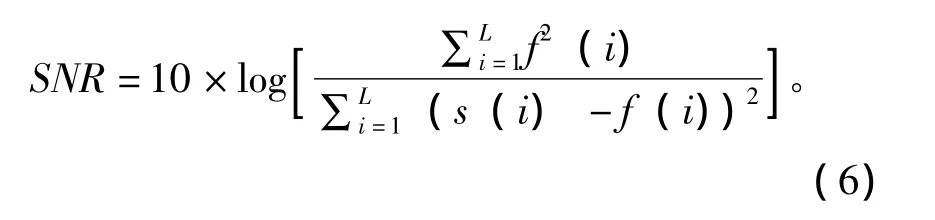

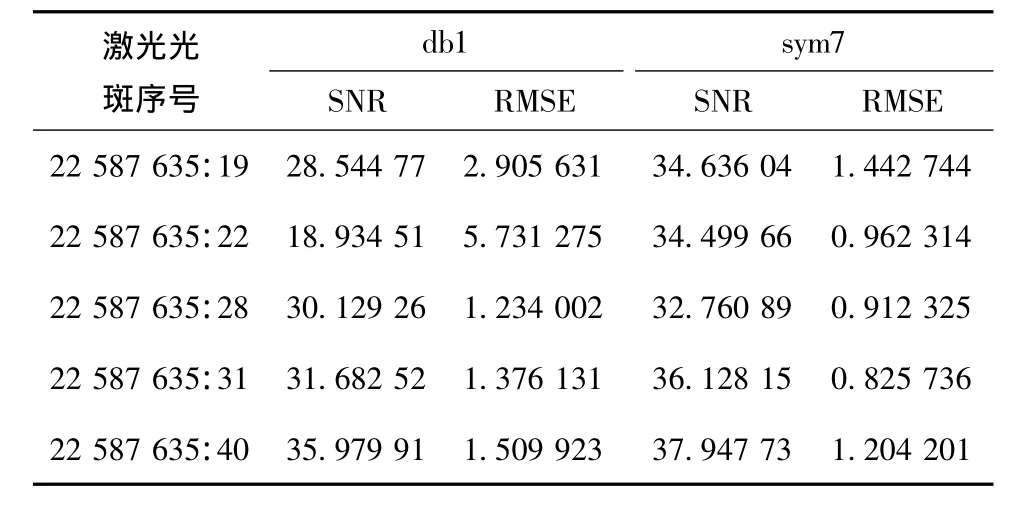
表2 小波变换波形数据处理结果Tab.2 Results of wavelet transform

图1 分别用db1和Sym7对波形进行去噪处理Fig.1 Denoised wave by db1 and sym7
图1中 (a)为用db1对数据去噪,(b)为用sym7对数据去噪,用此两种小波对GLA01_22587635:28去噪结果表明经过两种小波基去噪后波形都比原始波形平滑了,但经db1小波基去噪后的波形在波峰前后尚含有一定噪声,而经Sym7小波基去噪后的波形效果就比db1小波基效果好,波形更加平滑;同时表2中显示经db1小波基处理后的信噪比为 30.129 26,均方根误差为 1.234 002,经Sym7小波基去噪后的信噪比为32,760 89,均方根误差为0.912 325。观察比较表2中的所有数据发现对同一组数据Sym7小波基的信噪比比db1小波基的要高,而均方根误差比db1小波基的要低。信噪比越高,均方根误差越低说明信号的去噪效果越好。所以在处理大光斑激光雷达波形数据方面Sym7小波基比db1小波基更合适。
4 结论
本文对吉林长白山汪清林业局的经营区的大光斑激光雷达波形数据,通过比较分析发现db1小波基和Sym7小波基的去噪效果比db1小波基的好,更适合对大光斑激光雷达波形数据进行去噪处理。原始波形数据中的细节信号是高频突变信号,属于噪声,逐渐逼近于信号的低频部分,而小波变换恰恰可以起到低通滤波的作用,因此既可以有效保留信号频谱成分,又去除了噪声,克服了波形“重叠”现象。
本实验只是在数据中随机选取了5组数据采用里两种小波基进行研究,不排除偶然性,在今后研究中应该尽量对多组数据进行处理,降低偶然性误差,提高准确性和可信性;小波基有很多种,本文只是比较了其中两种小波,不排除其他小波基能更好的对数据进行去噪,比如高斯小波。
[1]刘经南,张小红.利用激光强度信息分类激光扫描测高数据[J].武汉大学学报(信息科学版),2005,34(6):696-700.
[2]Lázaro J C.Influence of thresholding procedures in ultrasonic grain noise reduction using wavelets[J].Ultrasonics,2002,40(8):263-267.
[3]Xu Y S,Weaver JB,Hedly D M.Wavelet transform domain filters:A spatially selective noise filtration technique[J].IEEE Transactions on Image Processing,1994,3(6):747-758.
[4]Da silva E A D,Ghanbari M.On the performance of linear phase wavelet transforms in low bit-rate image coding[J].IEEE Transactions on Image Processing,1996,5(5):689-705.
[5]孙仁山,李文彬,徐凯宏.基于小波变换的林业图像处理研究[J].森林工程,2005,21(1):4-6.
[6]邢艳秋,王立海.基于ICESAT-GLAS完整波形的坡地森林冠层高度反演研究——以吉林长白山林区为例[J].武汉大学学报(信息科学版).2009,34(6):696-700.
[7]Antonini M,Barlaud M,Mathieu P,et al.Image codingusing wavelet transform[J].IEEE Transactions on Image Processing,1992,1(2):205-220.
[8]胡 波,陈 恳,徐建瑜.一种基于新型小波包阈值的图像去噪方法[J].宁 波 大 学 学 报(理工版).2009,22(4):454-458.
[9]Labat D.Recent advances in wavelet analyses:Part 1.A review of concepts[J].Journal of Hydrology,2005,314(1-4):275-288.
