基于简化载荷谱法与雨流计数法的接触网疲劳寿命对比分析
2012-08-02毕继红陈花丽任洪鹏
毕继红,陈花丽,任洪鹏
(1.天津大学建筑工程学院,天津 300072;2.滨海土木工程结构与安全教育部重点实验室 (天津大学),天津 300072)
1 概述
电动车组高速运行时弓网耦合系统的动态受流对接触线产生较高的循环应力,动应力时程(应力谱)产生较大的波动,应力幅值很大,比低速时更容易发生疲劳破坏,因此对接触网进行精确的寿命预测至关重要。彭再恒[1]采用简化载荷谱法仅取应力谱的最大值和最小值,估算接触线在这个最大的应力循环下的疲劳寿命,不能精确预测高速运行时接触网的寿命。
雨流计数法简称雨流法[2],即把载荷谱曲线旋转90o,时间坐标轴竖直向下,数据记录犹如一系列屋面,从表面看上去好像雨流从载荷的峰谷处流下,凡起始于波谷(峰)的雨流遇到比它更低的谷(峰)值便停止,即上一段雨流被下一段雨流“截断”而形成一个全循环,故称为雨流计数法。雨流计数法能将载荷谱以离散载荷循环的形式表示出来,计数结果用应力幅值和应力均值来表示[3],广泛应用于随机载荷谱下的疲劳寿命估算。董乐义/罗俊[4]、周俊/童小燕[5]等人提出了雨流计数法在程序中的具体实现方法,简单有效并易于操作。
2 接触网疲劳寿命估算的2种方法
2.1 简化载荷谱法分析疲劳寿命
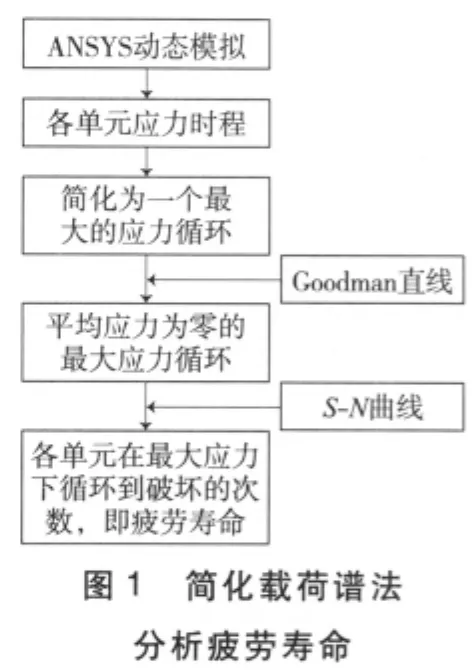
弓网耦合系统动态模拟得到的接触线各单元的动应力时程(即应力谱),是变幅应力谱,简化后再进行疲劳寿命估算,具体分析过程见图1,分析步骤如下。
(1)应力谱的简化
取应力时程的应力最大值和应力最小值,二者相减得到最大的应力幅。考虑到接触线单元的应力时程中除了最大的应力幅外,其他应力幅值较小,对疲劳寿命的影响可能较小,将应力谱简化为一个最大的应力幅,忽略其他应力幅值,计算在这个最大应力幅下的疲劳寿命。
(2)Goodman直线
应力时程简化后得到一个非零应力均值的应力循环,必须转换为零应力均值的应力循环(应力比为-1)才能使用S-N曲线计算疲劳寿命。本文利用Goodman直线[6]进行应力均值的转换

式中,S为等效零应力均值;Sa为循环应力幅值;Sm为循环应力均值;Su为材料的极限强度。
(3)S-N曲线
循环应力均值修正后,就可使用应力比为-1时的基本应力-寿命曲线,即S-N曲线。本文按照文献[1]的方法对S-N曲线进行简化和修正,最终的S-N曲线的表达式为

式中,S-1为材料的疲劳极限;Ks1、Ks2是考虑各种实际因素引入的分散系数。
(4)接触线的疲劳寿命
由式(2)得到接触线单元i在最大应力幅值Si下达到破坏的循环次数Ni,即接触线各单元的安全运行次数,本文中以列车每天运行100次计算,最终寿命的折算年限是Ni/(365×100)。
2.2 雨流计数统计载荷谱法分析疲劳寿命
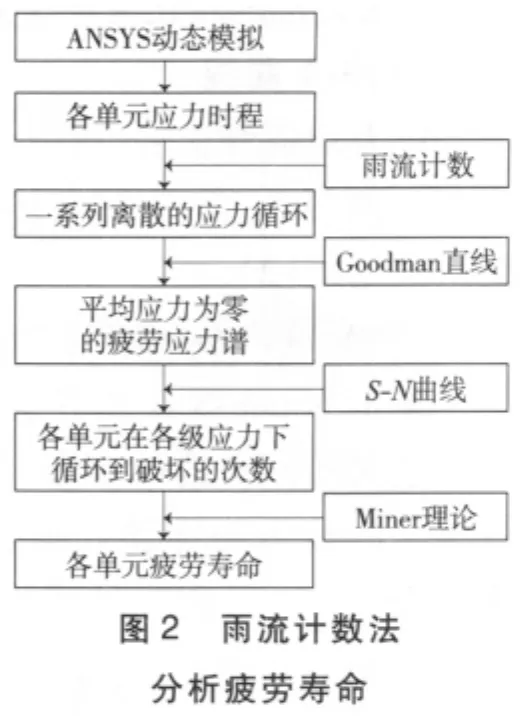
为了精确估算接触线的疲劳寿命,采用改进的雨流计数法,对接触线各单元的动应力时程进行计数统计,得到各级应力循环,计算接触线各单元在变幅应力循环下的疲劳寿命,具体过程见图2,分析步骤如下。
(1)雨流计数法统计应力谱
将各单元的应力时程储存于一个二维数组中,二维数组的每行表示同一时刻接触线各单元的应力,每列表示接触线某一单元的应力时程,具体实现过程如下:
①相邻等值数压缩和谷峰值提取。分别对二维数组的每列判断应力时程前后2个元素是否相等,若相等则只保留一个;判断二维数组每列相邻数值的差的乘积是否大于零,若大于零则提取峰(或谷)值。
②谷峰值调整。对二维数组的每列判断峰谷值点总数是否为偶数,若为偶数则去掉最后一个点。判断首尾点是峰值还是谷值,若是峰值,则使首尾两点的值都取二者中的较大者;若是谷值,则使首尾两点的值都取二者中的较小者。
③对接。寻找调整过的应力时程二维数组每列的最高波峰(最低波谷)点,将应力时程的每列从该点处截断,将左段的起点与右段的末点对接,使新的应力时程首尾皆为最高波峰(最低波谷)点。
④用四峰谷值法进行一次雨流计数,4个点的选取遵循单向选取、循环进行的原则提取循环的应力幅值和应力均值,并记录相应的应力循环数。
⑤雨流计数循环。对一次雨流计数后剩下的点编制循环命令流,继续提取应力循环直至剩下3个点(即是数组中最值构成的整循环)为止。
⑥循环统计。去除幅值很小的可以忽略的应力循环,并按照1 MPa的应力幅分级范围统计不同应力幅下的应力循环数目。
(2)Goodman直线
由于应力均值对疲劳累积损伤的影响,用Goodman直线对雨流计数的结果进行应力均值修正,将非零应力均值的应力范围转化为零应力均值的应力范围。
(3)S-N曲线
应力均值修正后,利用S-N曲线得到单元j在第i级应力循环Sij下,达到破坏的循环次数Nij,S-N曲线表达式见式(2)。
(4)Miner线性累积损伤理论
基于Miner线性疲劳累积损伤理论,对各级应力循环造成的损伤进行累加,利用破坏准则得到接触线各单元的疲劳寿命值。根据Miner疲劳累积损伤理论[7]有

式中,kj为单元j的应力水平级数;nij为单元j的第i级应力循环Sij在应力谱一个循环中发生的次数,由雨流计数法得到;Nij为单元j在第i级载荷Sij单独作用下的破坏循环数,由S-N曲线得到;Bj为单元j在应力载荷谱作用下达到疲劳破坏所需的载荷谱块数。
(5)接触线的疲劳寿命
由式(3)得到Bj,即接触线各单元的安全运行次数,最终寿命的折算年限是Bj/(365×100)。
2.3 2种方法比较
因应力幅值越小疲劳寿命越大,简化载荷谱法估算接触线的疲劳寿命,只取应力谱的最大应力幅值,忽略其他应力幅值,计算结果可能会有一定程度的偏大。雨流计数统计载荷谱法精确统计接触线单元的应力谱,通过疲劳损伤理论得到疲劳寿命,计算结果可靠。
3 接触网疲劳寿命分析算例
3.1 算例介绍
算例采用10跨单锚段弹性链形接触网,模型如图3所示。受电弓按三元弓模拟,参照文献[8]选取基本参数见表1。为了使计算达到稳定收敛,划分接触线的网格时,对定位点左右一个吊弦间距的范围内(即定位点左右各4.5 m)加密网格,单元长度为0.25 m,其余接触线单元长度为0.5 m。

图3 弹性链形柔性接触网模型

表1 算例基本参数
3.2 2种算法疲劳寿命比较
本算例分别用简化应力谱和雨流计数统计应力谱的方法,对接触线各个单元进行疲劳寿命估算,取一跨内各单元的寿命最小值作为该跨的最终寿命。计算结果只取中间4跨平稳段的疲劳寿命和在跨内取得最小寿命的具体位置,见表2。
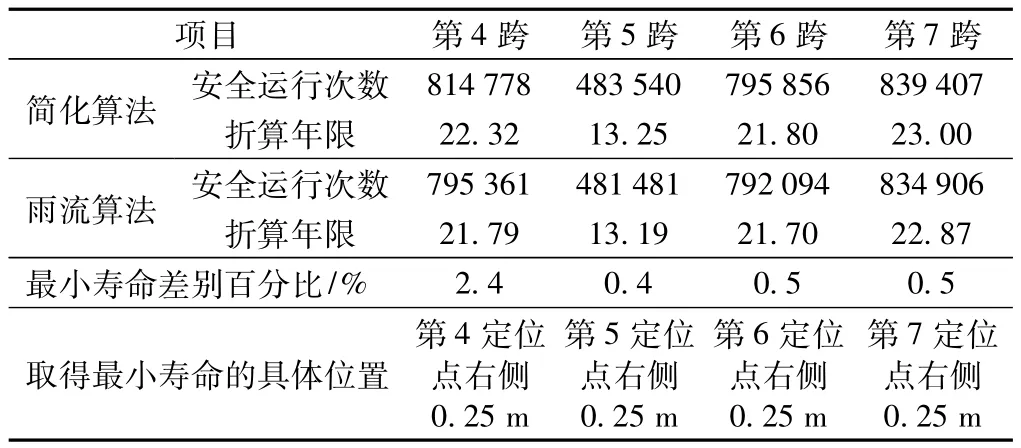
表2 2种算法疲劳寿命比较
可以看出,每跨定位点右侧第一个单元的疲劳寿命最小,简化算法所得疲劳寿命稍大于雨流算法,最大相差仅2.4%,说明若不关心接触线上其他位置的疲劳寿命,只关心每跨的最终疲劳寿命,用简化载荷谱法分析疲劳寿命能达到一定精度要求。
3.3 2种算法疲劳寿命差别较大的单元
现分析除定位点右侧接触线单元以外,2种算法所得疲劳寿命差别较大的单元位置。以第6跨为例,提取简化算法寿命高于雨流算法寿命40%以上的单元位置,见图4中浅色部分。
可以看出,寿命差别大的位置包含吊弦右侧附近的单元和定位点左右一个吊弦间距范围内的单元,分析图4中标示位置的单元应力时程,如图5所示。

图4 第6跨两种算法寿命差别大于40%的位置
图5(a)~5(c)为2种算法疲劳寿命差别大的单元应力时程,图5(b)和图5(c)是位于吊弦点右侧的接触线单元,图中有应力峰值远远大于其他时刻的应力值,这个应力最大值发生在受电弓经过该单元时,除此之外,还有一些较大的应力值,应力时程波动较大;图5(a)是位于定位点左右一个吊弦间距范围内的接触线单元,应力时程虽没有吊弦点右侧单元波动大,但有几个应力值大小接近应力最大值,在疲劳寿命估算时不能忽略。简化载荷谱法只取应力时程中的应力最大值,忽略其他的应力循环,没有雨流计数统计载荷谱法可靠。在定位点左右一个吊弦间距范围内和吊弦点右侧附近的某些单元,简化载荷谱法所得寿命值高于与雨流计数统计载荷谱法所得寿命的40%以上,需使用雨流计数统计载荷谱法。
图5(d)为一般接触线单元的应力时程,仅有一个应力最大值,其他的应力值都很小,可以忽略不计,2种算法疲劳寿命差别不大,可以使用简化载荷谱法估算接触线的疲劳寿命。
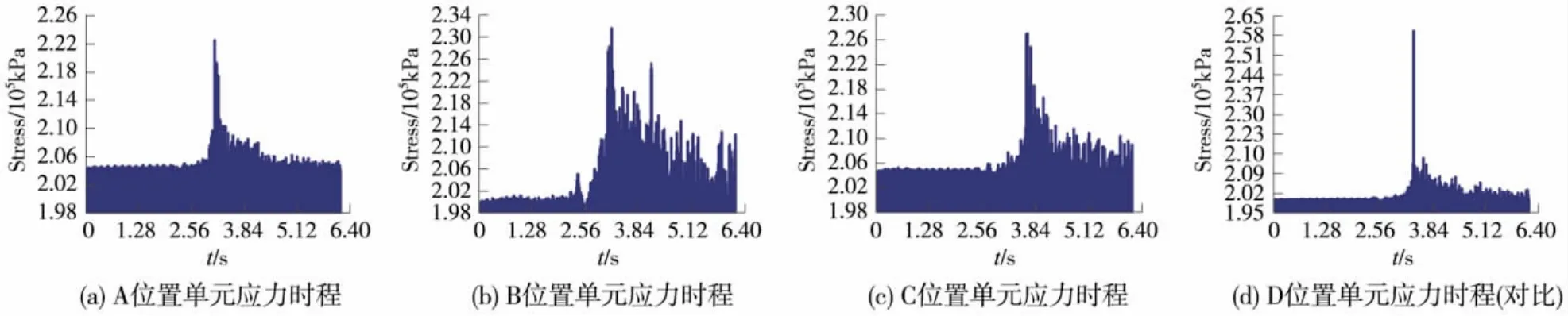
图5 第6跨单元应力时程
4 结论
本文分析了简化载荷谱法与雨流计数统计载荷谱法估算接触网疲劳寿命,通过算例分析可以得到以下结论。
(1)简化载荷谱法与雨流计数统计载荷谱法寿命差别大的单元,其应力时程都有一个明显的应力最大值,此外还有一些不可忽略的较大应力值。简化载荷谱法估算接触线疲劳寿命只取应力谱的最大应力幅值,忽略其他应力幅值,所得疲劳寿命偏高。
(2)若取接触线一跨内各单元的寿命最小值作为该跨的最终寿命,2种算法所得疲劳寿命差别很小,若不关心接触线上其他位置的疲劳寿命,只关心每跨的最终疲劳寿命,用简化载荷谱法分析疲劳寿命能达到一定精度要求。
(3)在定位点左右一个吊弦间距范围内和吊弦点右侧附近的接触线单元,简化载荷谱法所得寿命值高于与雨流计数统计载荷谱法所得寿命的40%以上,使用雨流计数统计载荷谱法估算接触线疲劳寿命更为精确;其余的接触线单元可近似使用简化载荷谱法估算疲劳寿命,以节省计算空间和时间。
[1]彭再恒.应用TCL/TK语言对弓网耦合系统的界面开发及相关疲劳分析[D].天津:天津大学,2010.
[2]蒋荟,杨晓华.实时雨流计数法的“三变程”计数原则[J].航空计算技术,2008,38(5):5-7.
[3]田军,李强.改进的雨流法实时计数模型[J].北京交通大学学报,2009,33(1):28-31.
[4]董乐义,罗俊,程礼.雨流计数法及其在程序中的具体实现[J].航空计算技术,2004,24(3):38-40.
[5]周俊,童小燕.雨流计数的快速实现方法[J].科学技术与工程,2008,8(13):3545-3547,3558.
[6]陈传尧.疲劳与断裂[M].华中科技大学出版社,2002.
[7]赵少汴.常用累积损伤理论疲劳寿命估算精度的试验研究[J].机械强度,2000,22(3):206-209.
