C54x系列DSP的快速双精度平均算法实现

张 华，刘 伟，吴友宇

(1.武汉理工大学信息工程学院，湖北 武汉 430070;2.中船重工710所，湖北 宜昌 443003)

德州仪器(texas instruments，TI)公司生产的C54x系列数字信号处理器(digital signal processor，DSP)以低价高效的特点得到了电子工程师的喜爱。TI公司也为DSP配套了库函数[1]，方便开发人员的调用和移植，但库函数作为通用代码，对其运行效率考虑较少。为了提高程序运算效率，满足实际中1/3OCT分析的实时要求，笔者设计和实现了一种采用C54x系列DSP快速双精度求平均算法。

1 DSP快速求平均的原理

1.1 DSP对快速求平均的硬件支持及相关指令

C54x系列DSP总线宽度为16位(单字)，内部有两个40位的累加器，分别称为A和B。两个累加器都支持双精度指令。C54x系列DSP累加器A和B框图[2]如图1所示。

图1 DSP累加器A和B框图

16位DSP累加器装载的临时数据如果数值大于0xFFFFFFFF，就会产生溢出错误;而16位DSP存储器装载的数据如果数值大于0xFFFF，就会产生溢出错误[3]。

以往基于DSP处理器SUBC指令的多字除法算法大多采用若干单字除法组合的方法[4]，操作比较繁杂，没有利用SUBC指令支持双精度除法的功能。笔者分两步来实现快速求平均运算:先用累加器保存源数据的累加结果，以作为被除数，再将累加次数作为除数，进行快速双精度除法。该方法在源数据数值不超过双字、累加次数不溢出超过单字且累加和不超过3个字时有效。如果不能同时满足以上3个条件，则要采用多个数据存储区暂存累加结果，或将源数据分别乘以被除数的倒数[5]再进行累加。

1.2 双精度累加运算原理

设有双字数据源 S1，S2，…，Sy(y ＜ 65 536)，每个数据分成高字和低字，即S1=S1H×0x10000+S1L，S2=S2H × 0x10000+S2L，…，Sy=SyH ×0x10000+SyL。双精度累加运算时，累加器A装载S1L，S2L，…，SyL的累加结果，累加器 B装载S1H，S2H，…，SyH的累加结果。然后将AH与累加器B累加的结果再装载进累加器B。最后得到的双字数据源累加结果，如式(1)所示。

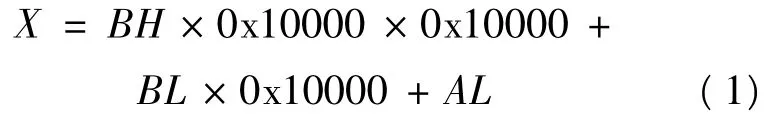
式(1)中X数据的宽度为3个字。

1.3 双精度除法运算原理

以上介绍了累加结果X的计算方法，在双精度除法中，X为被除数，累加次数Y为除数，并且2≤Y＜65 536，Z为商。由于求的是平均运算，因此，商不会超过数据源的最大值。

借鉴将双字被除数拆解成高字和低字，再分别与除数运算的思想[6－7]，先将 X 拆解成高字XH、中字XM和低字XL，如式(2)所示。

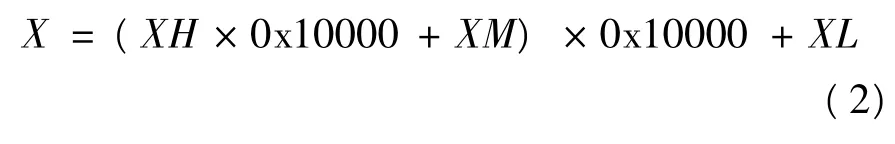
由式(2)可推出三字除法，如式(3)所示。

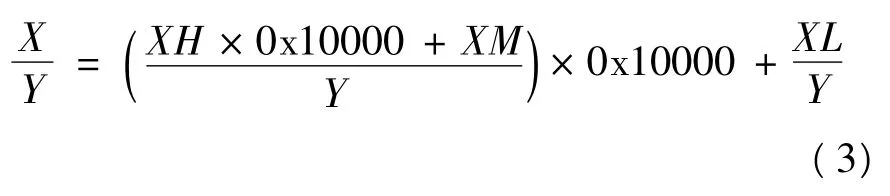
对比式(1)与式(2)可知，累加器B的高字BH已经装载了XH，低字BL已经装载了XM。因为能保证不会溢出，可以直接让B除以Y。程序代码如下:

RPT #15

SUBC @tempB，B ;B为被除数，@tempB为除数。

利用SUBC指令进行快速除法的原理已有介绍[8－9]，在此不再叙述。

将式(4)代入式(3)，得到式(5)。

对比式(1)与式(2)可知，累加器A的低字AL已经保存了XL，现在将VH装载进累加器A的高字AH中。因为能保证

式(6)中，WH×0x10000相当于将WH左移16位。实际操作中是将WH装载到Z的高字ZH，而将WL项的结果装载到ZL。

由式(1)到式(6)的推导可以看出，高字除法产生的余数，参与了低字除法，最后的总误差来自余数VL，是定点运算不可避免的，计算误差降到不会溢出，可以直接让A除以Y，得到的商WL自动保存在AL，余数VL自动保存在AH。最后得到的求平均算法如式(6)所示。了最低。

2 平均算法程序流程图及关键代码

根据上述双精度除法运算原理，采用DSP快速求平均算法的程序流程如图2所示。

图2 求平均算法程序流程图

关键代码如下:

3 算法测试

3.1 算法误差测试

双精度除法运算原理在C54x系列DSP编译平台CCS(code composer studio)仿真模式下进行代码验证。为了方便误差测试，作如下设置:源数据 Xi(i=1，2，…，且 i＜65 536)放在 FFT_G_k 起始的存储单元中。设置程序循环运行1 024次，以t∈(1，2，…，1 024)来标记循环中的某一次。累加数从相对起始地址St开始按递增顺序从Xi中提取，并且St数值依次存放在fm_K起始的奇数存储单元中。每次求平均运算的累加次数Yt依次放在fm_K起始的偶数存储单元中。将每次运算的平均结果Zt按递增顺序保存在_oct_data1起始的存储单元中。如果代码运算正确，Zt、Yt与Xi应满足式(7)。

式(7)不能产生直观的验证结果，为此进一步将Xi、St及 Yt作简化设置，如式(8) ～式(10)所示。

由式(7)～式(10)联合得到简化后的验证表达式，如式(11)所示。

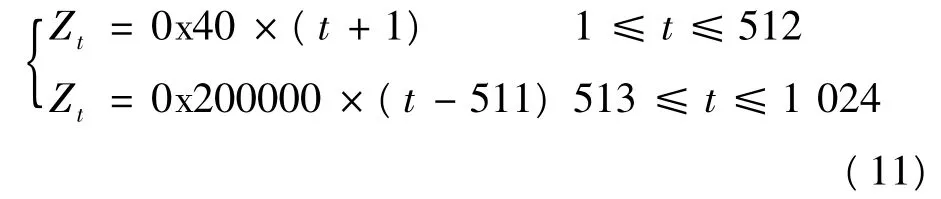
在CCS中以图形界面显示_oct_data1起始的存储单元，以1步进，并作一些简化设置，如图3所示。

图3 CCS对求平均算法测试结果的图形显示

为了直观显示，图3(a)纵坐标显示的Z't为Zt除以0x40的结果，图3(b)纵坐标显示的Z't为Zt除以0x200000的结果;又因为CCS图形界面的X轴以0起始，设置t'=t－1。如果算法正确，代码运行结束后图3中纵坐标Z't与横坐标t'应满足式(12)。

通过分析图3可知，波形函数满足式(12)，由此推出求该代码对1～1 024之间的数据量求平均，其误差几乎为0。

3.2 代码效率测试

运行该代码所需的时钟数，可通过CCS配套的View Clock工具进行测试，最后得到循环次数与执行时钟的关系如表1所示。

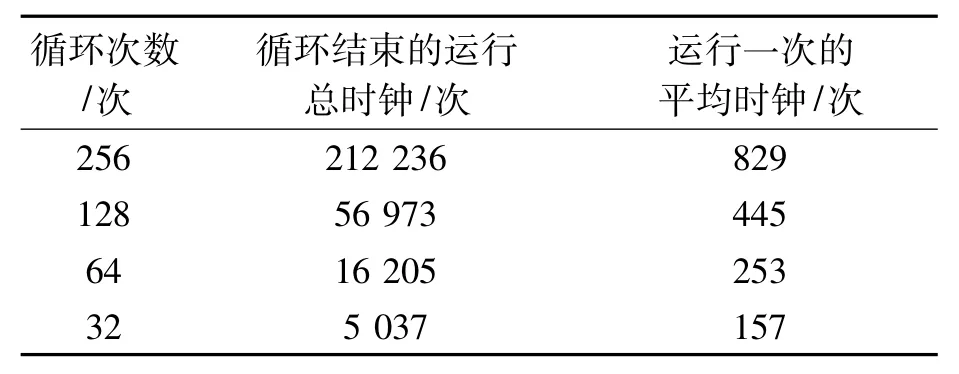
表1 快速求平均算法代码循环次数与执行时钟的关系

CCS中采用C语言进行求平均运算，得到相应的循环次数与执行时钟关系如表2所示。

表2 C语言求平均运算循环次数与执行时钟的关系

从表1和表2可知，运行一次的平均时钟等于循环结束的运行总时钟除以循环次数。循环次数不同，运行一次的平均时钟也不同。因为在求平均运算所费时钟数一定的情况下，循环次数越少，执行累加运算的时钟越少[10－11]。通过手工计算可以粗略得知，快速求平均算法执行一次的平均时钟是421，C语言求平均运算执行一次的平均时钟是12 516，两者相差约30倍。由此可见快速求平均算法为系统实时运行提供了保障。

4 结论

通过对快速求平均算法的测试，表明了其正确性和实时性，为实时处理系统做了可靠的铺垫。所研究内容已移植于某项目的1/3OCT分析中。

[1] Texas Instruments Incorporated.Optimized DSP library for C programmers[DB/OL].[2011 － 10 － 18].http//www.Texas Instruments Incorporated.

[2] 戴明桢，周建江.TMS320C54x DSP结构、原理及应用[M].北京:北京航空航天大学出版社，2007:28－29.

[3] 张家田，刘新英，严正国.DSP的定点溢出处理技术[J].中国科技信息杂志，2008(24):83 －85.

[4] 张文英，史小军，张端金.TMS320C2XX型数字信号处理器多字除法的实现[J].郑州大学学报:自然科学版，2001(6):68－71.

[5] NENADIC N M，MLADENOVIC S B.Fast division on fixed－point DSP processors using Newton－raphson method[C]//EUROCON 2005 The International Conference on“Computer as a Tool”.Belgrade:Serbia and Montenegro，2005:705 －708.

[6] 赵慧，张淼，冯垛生.TMS320C2XX(DSP)中无符号多字除法程序的实现[J].河南科学，2005，23(1):124－126.

[7] AGGARWAL N，ASOOJA K，VERMA S S，et al.An improvement in the restoring division algorithm[C]//International Conference on Computer Science and Information Technology.Beijing:[s.n.]，2009:146 －149.

[8] 邹彦，唐冬，宁志刚，等.DSP原理及应用[M].北京:电子工业出版社，2006:153－154.

[9] 丁电宽，万毅.除法运算在定点DSP中的实现[J].安阳师范学院学报，2006(2):29－31.

[10] 陈雪梅，韩洁琼.C语言可视化编程环境的设计与实现[J].武汉理工大学学报:信息与管理工程版，2010，32(4):561 －564.

[11] MULLER J M，TISSERAND A，DINECHIN D，et al.Division by constant for the ST100 DSP microprocessor[C]//17th IEEE Symposium on Computer Arithmetic.USA:Cape Cod Massachusetts，2005:124 –130.