压电悬臂板的非线性振动控制*

邱志成 凌德芳

(华南理工大学机械与汽车工程学院，广东广州510640)

航天器上的柔性附件(如太阳能帆板结构)具有质量轻、刚度低和阻尼弱等特点，在航天器完成机动、转向、变轨等动作或者受到外部干扰的时候，容易产生振动．若不进行有效的抑制，引起的振动将会持续很长时间，这不仅影响航天器姿态的稳定和定向精度，甚至可能造成结构破坏．因此，需进行柔性板结构振动主动控制研究［1-2］．

柔性板结构振动主动控制多采用压电陶瓷片或压电薄膜作为传感器和驱动器．压电智能板结构建模研究可采用有限元方法［3-5］．为了实现压电悬臂板弯曲和扭转模态振动的测量和驱动控制，需研究压电传感器/驱动器配置．关于压电传感器/驱动器配置位置的研究方法有:根据可控可观Gram矩阵，利用遗传算法优化［6-7］;以最小闭环系统的H2范数作为优化准则［8］;利用一种能量耗散方法实现位置的优化配置，保证较好的能控性和能观性，且同时考虑剩余模态以限制控制溢出［9-10］．

压电挠性板的振动主动控制采用的控制算法主要有:正位反馈控制［11］，鲁棒控制［12］，自适应控制［13］，模糊控制［14］等．控制的目的是快速抑制弯曲和扭转模态振动．从现有研究可知，柔性悬臂板的大幅值振动可快速衰减到较小幅值，但小幅值振动会持续很长时间．为保证柔性板的大幅值和小幅值振动快速衰减，考虑采用非线性控制算法［15-16］．

文中针对压电悬臂板的弯曲和扭转模态的振动，进行了建模、压电传感器/驱动器配置优化，并提出一种非线性控制算法，同时进行了振动控制实验研究．

1 系统模型

采用矩形板单元进行压电柔性悬臂板建模．矩形板单元有4个节点，每个节点包括挠度w、绕x轴和y轴的转角θx和θy共3个自由度．矩形板单元共12个自由度．

对压电悬臂板结构进行单元划分，经过单元组装后，并考虑阻尼项D，得整体动力学方程

式中，M、K分别为整体质量和刚度矩阵，d为整体位移矢量，FA为压电驱动力矢量，FA=KavV，其中Kav为压电驱动系数矩阵，V为驱动电压矢量．

单元组装后的压电传感方程为

式中，Ksv为压电传感系数．

引入模态坐标q，则由模态坐标变换d=Φq，最终得到系统的状态空间模型为

考虑系统前5阶模态，系统状态矢量X(t)维数为10．根据悬臂板的结构尺寸，最终得到的系统模型中，第1、3、4阶为前3阶振动模态弯曲模态，第2、5阶为前2阶扭转模态．对于弯曲振动，取第1、3阶为控制模态，第4阶为剩余模态;对于扭转振动，第2、5阶都取为控制模态，不考虑剩余模态．

2 压电传感器/驱动器配置优化

采用能量耗散率的方法对压电传感器/驱动器进行位置的优化配置．该方法在系统可控性和可观性Gram矩阵基础上描述性能指标，并对弯曲振动考虑了剩余模态的作用以限制控制溢出．这里只讨论对驱动器的位置优化，传感器的位置优化利用同样的原理可以得到．

系统的能控Gram矩阵定义如下

第i阶模态的能控Gram矩阵分量为［9］

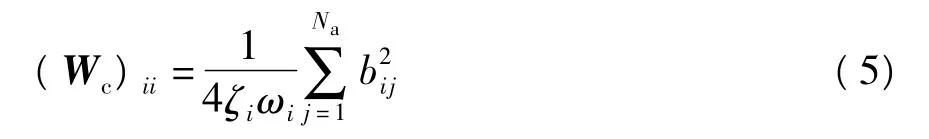
式中，i=1，2，…，N，N+1，…，N+NR，ξi为第 i阶模态阻尼比，ωi为第i阶模态频率，bij为B中对应参数，Na为驱动器个数，N为控制模态阶数，NR为剩余模态阶数，j表示第j个驱动器．

对于控制模态(i=1，2，…，N)，能控 Gram 矩阵分量表示为()ii，对于未控制的剩余模态(i=N+1，N+2，…，N+NR)，能控 Gram 矩阵分量表示为(WRc)ii．对弯曲振动，考虑了剩余模态，采用位置优化准则［9］:

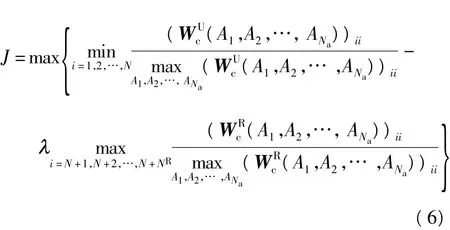
对扭转振动不考虑剩余模态，采用优化准则为

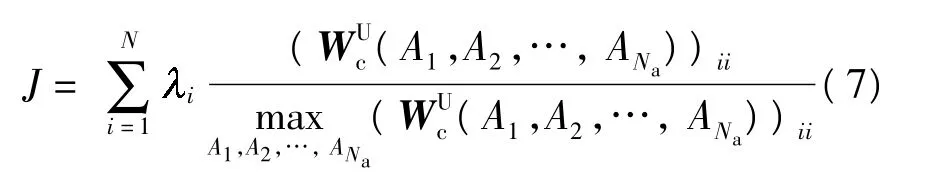
研究时共考虑悬臂板的前5阶模态．对弯曲振动，考虑前2阶弯曲模态为控制模态，第3阶弯曲模态为剩余模态．由于第3阶弯曲模态对弯曲振动的影响较小，故加权值取=0.3，驱动器个数取为1，由式(6)求得压电驱动器在悬臂板各个配置位置上弯曲模态性能指标如图1(a)所示．对扭转振动，考虑第1、2阶扭转模态为控制模态，无剩余模态．加权值取1=0.62=0.4，驱动器个数取为1，由式(7)求得压电驱动器在悬臂板各个配置位置上扭转模态性能指标如图1(b)所示．指标越大，表明驱动器控制作用越强．

图1 驱动器配置性能指标Fig．1 Performance index of actuator placement

分析图1(a)可知，对于弯曲模态，在x方向，在靠近悬臂板根部，控制效果最好．在y方向，两边缘稍里性能指标最好．由图1(b)的优化结果分析可知，对于扭转模态，在x方向，在悬臂板的根部和中间处，控制的性能指标较好;在y方向，总的趋势是越靠近中心处性能指标绝对值越小，并在板的中心达到最小值．

传感器的位置优化利用同样的原理可以得到，此时在系统可观性Gram矩阵基础上描述性能指标，并可以考虑剩余模态以限制观测溢出．

3 系统描述

建立压电悬臂板实验系统如图2所示，其中的压电驱动器和传感器的粘贴位置依据位置优化配置计算结果．在图2中，压电片1－8粘贴在悬臂板的靠近根部位置，信号线并联连接作为一路弯曲模态驱动器．压电片9粘贴在靠近悬臂板根部宽度方向的中心位置，作为弯曲模态传感器．将弯曲模态传感器布置在宽度方向中心处，还考虑到在悬臂板宽度方向的几何中心处无扭转振动信号．

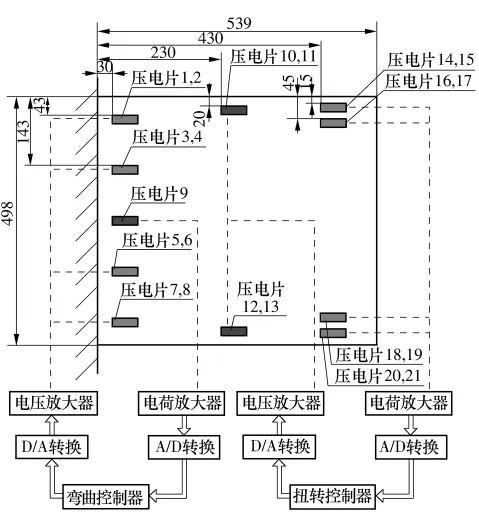
图2 压电悬臂板系统图(数值单位:mm)Fig．2 System diagram of piezoelectric cantilever plate

压电片14、15、20和21组成一路扭转模态传感器．考虑到在根部已经布置了多片的弯曲模态驱动器和传感器，为尽量减少弯曲振动控制和扭转振动控制之间的相互耦合作用，因此将扭转模态传感器布置在远离弯曲模态驱动器的末端边缘处．压电片16，17，18和19同样可以组成一路扭转模态驱动器或者扭转模态传感器．

压电片10－13作为扭转模态驱动器，布置在悬臂板长度方向中部，宽度方向靠近边缘．此时扭转模态压电驱动器和传感器异位配置，克服了因同位配置产生的局部应力集中导致的局部刚化即局部控制问题．

三是积极落实最严格水资源管理制度。全面建成覆盖全省的水资源管理控制指标体系，逐步建立最严格水资源管理考核制度。加强水资源论证、取水许可和水资源费征收管理，开展《水功能区划》《吉林省用水定额》修订，启动地下水普查工作，加强节水型社会建设。

除压电片9单面粘贴外，其它压电片皆双面对称粘贴，且正反面信号极性反相连接．压电片1－8分成4对通过信号线并联组成一路弯曲模态驱动器．压电片14－21沿板宽度方向中心线对称布置，对称位置上压电片输出的弯曲振动信号同相，扭转振动信号反相，将对称位置上压电片的输出信号线按相反极性连接在一起，弯曲模态振动信号被相互抵消，只输出扭转振动信号．压电片10－13共两对压电片组成扭转模态驱动器，压电片10、11和压电片12、13沿板宽度方向中心线对称布置，且输入电压反相，这样在板沿宽度方向中心线两侧产生相反的驱动力矩，从而实现对扭转振动的控制．对于扭转模态，这里压电片采用了姿态角为0°的反对称布置方式，相比于姿态角为45°的双面反对称布置方式［11］，这种布置方式粘贴方便，便于模型的建立，且可双面粘贴，占用空间少，允许配置更多的压电片以提高驱动力．

图2所示系统共有弯曲振动和扭转振动两个控制通道．弯曲模态和扭转模态压电传感器分别检测悬臂板的弯曲和扭转振动信号，经电荷放大器放大和A/D转换，进入计算机，运行相应算法后产生弯曲和扭转振动控制信号，经过D/A转换，将控制电压分别送入弯曲模态和扭转模态压电驱动器生成驱动力矩抑制悬臂板的弯曲和扭转振动．

4 控制算法

在设计压电悬臂板的控制方法时，考虑采用比例积分(PD)算法和非线性算法．PD算法为

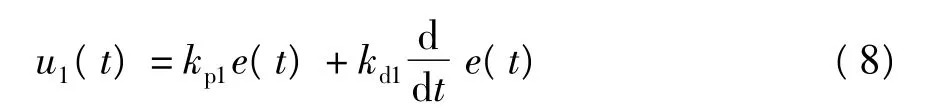
式中，kp1为比例增益，kd1为微分增益，e(t)为误差信号，u1(t)为PD控制量．

本系统中包括结构的大变形、驱动器的饱和、死区、各向异性以及粘贴层不均匀等非线性因素．另外，从压电挠性结构的试验结果来看，采用线性控制方法，大幅值的振动可以较快地被抑制到较小幅值，但平衡点附近的低阶模态频率上的小幅值振动很难快速衰减．为了快速抑制振动，尤其是加快小幅值振动的衰减速度，提出一种非线性控制算法进行控制．

该算法是将随误差与时间变化的非线性增益与线性增益PD控制器结合，得到非线性控制律

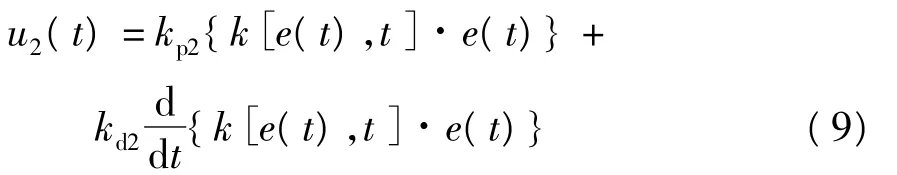
非线性增益k［e(t)，t］采用非线性函数构造为

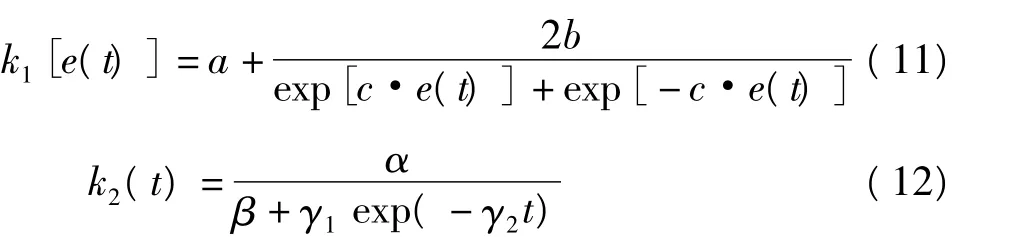
式中，a、b、c、α、β、γ1、γ2为调整参数，k1［e(t)］和k2(t)分别为随误差和时间变化的非线性增益．

当e(t) 0时，k1［e(t)］取最大值 a+b;当e(t) ±∞时，k1［e(t)］取最小值 a;c用于调整k1［e(t)］变化的速率，c越大，变化速率越快．k2(t)随时间变化，当 t 0时，k2(t)取最小值 α/(β+γ1);当 t + ∞ 时，k2(t)取最大值 α/β;γ2用于调整k2(t)变化的速率．各参数的选择应使k［e(t)，t］限制在一定的范围内，以保证系统的稳定性，具体参数可在实验中调整．

由式(9)－(12)可知，对于大幅值振动，误差较大时，控制增益相应减小，不至于带来系统的稳定性和控制溢出问题;对于小幅值振动，当误差变小时，k1［e(t)］增大，并且 k1［e(t)］被设定在［a，a+b］之内，变化的速率也是可调的，这样就保证了当振动幅值下降时，控制增益相应增大，从而控制量的下降是个较平缓的过程，且在小幅值振动仍然有较强的控制量，使得小幅值振动快速衰减．

k2(t)则随时间的增加而增加，且变化速率可调，变化范围被限制在了［α/(β+γ1)，α/β］之间，这样就保证了随着时间的增长，振动衰减到较小时，增益变大，从而系统仍然有较强的控制量．这样，通过对k1［e(t)］和k2(t)的调整，充分发挥了系统的控制能力，特别是对小幅值振动的抑制作用．

对于PD控制算法，只要将比例增益kp1和微分增益kd1限制在一定的范围内，即可保证系统的稳定性．文中非线性控制算法是将非线性增益与线性增益PD控制器结合，因此只要同样将非线性增益与固定比例增益的乘积k［e(t)，t］·kp2以及非线性增益与固定微分增益的乘积k［e(t)，t］·kd2限制在一定的范围内，即可保证系统的稳定性．

5 实验研究

压电悬臂板实验台照片如图3所示．悬臂板本体材料为环氧树脂，弹性模量 Eb=34.64 GPa，密度ρb=1840 kg/m3．压电片的粘贴位置尺寸如图2所示，压电片的几何尺寸为50 mm×15 mm×1 mm，弹性模量和压电应变常数分别为Ep=63 GPa和d31= －166 ×10－12m/V，密度为 ρp=7650kg/m3．电荷放大器由江苏联能电子有限公司生产，型号:YE5850．设定弯曲振动测量的电荷放大器灵敏度82.2 pC/单位，输出档位1mV/单位;设定扭转振动测量的电荷放大器灵敏度33.2 pC/单位，输出档位1 mV/单位．研制的压电驱动电路中放大器芯片型号为APEX PA240CX，可将D/A转换后的－5V～+5V电压信号放大到－260～+260V．数据采集卡采用台湾泓格ICP DAS数据采集卡，型号为PCI-1800H．

图3 实验装置照片Fig．3 Photo of the experimental setup

在建立实验平台过程中，由于测量、加工、安装、压电片的粘贴等因素的影响，对弯曲和扭转振动的测量和驱动并不是完全解耦的．此外，在实际的测量及控制中还存在着各种外界干扰和高频模态及测量噪声．所以需要对振动信号进行低通滤波处理后再送入控制器．对于弯曲振动信号，设计截止频率为8Hz的4阶Butterworth滤波器．对于扭转振动控制，设计截止频率为15 Hz的4阶Butterworth滤波器．

由于弯曲和扭转振动测量信号的解耦并不完全，在扭转振动压电传感器输出中包含一阶弯曲振动信号成分，因此设计阻带频率为3.75 Hz的带阻滤波器滤除一阶弯曲振动信号．

由于扭转振动传感器和驱动器采用异位配置，并且经过滤波器、模数转换和计算机离散控制量等环节都会引起信号时延．因此进行了移相处理，修正滞后相位．

实验研究包括激励弯曲和扭转模态的自由振动，PD控制和非线性控制算法的主动振动控制．

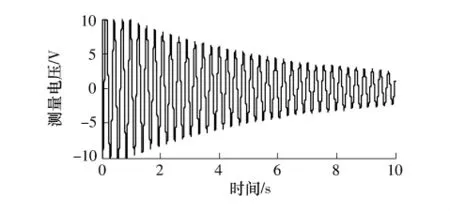
图4 第1阶弯曲模态自由振动时域响应Fig．4 Time-domain response of the vibration of the first bending mode

图5 第1阶弯曲模态振动PD控制Fig．5 PD control of the vibration of the first bending mode

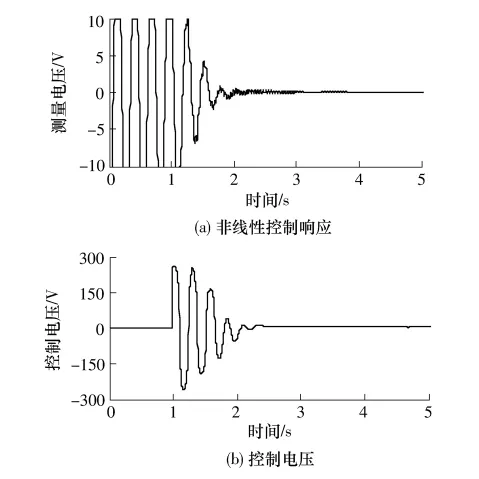
图6 第1阶弯曲模态振动非线性控制Fig．6 Nonlinear vibration control of the first bending mode

外界激励下弯曲模态自由振动时域响应曲线如图4所示，第1阶弯曲模态频率为3.75Hz．图5(a)为采用PD控制算法的第1阶弯曲模态振动控制响应曲线，图5(b)为对应的控制电压．图6(a)为采用非线性控制算法的第1阶弯曲模态振动控制响应曲线，图6(b)为对应的压电驱动器控制电压．比较图6和图5可知，采用PD算法和非线性算法在大幅值振动时，施加的控制电压几乎相同，但对小幅值振动由于采用了非线性控制算法，施加的控制电压高于PD控制，使得小幅值振动快速衰减．对弯曲模态振动的抑制效果优于PD算法．

图7为激励下扭转模态自由振动响应曲线，第1阶扭转模态频率为8.0 Hz．图8(a)为采用PD控制的扭转模态振动控制响应曲线，图8(b)为相应的控制电压．图9(a)为采用非线性控制算法的扭转模态振动控制响应曲线，图9(b)为相应的控制电压．比较可知采用文中的压电传感器和驱动器配置可以有效抑制扭转模态的大幅值振动，但PD算法的小幅值振动持续时间较长，非线性算法对扭转模态振动的控制效果更好，特别是小幅值扭转振动可以很快得到衰减．

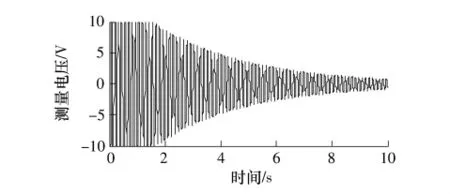
图7 第1阶扭转模态自由振动时域响应Fig．7 Time-domain response of the vibration of the first torsional mode

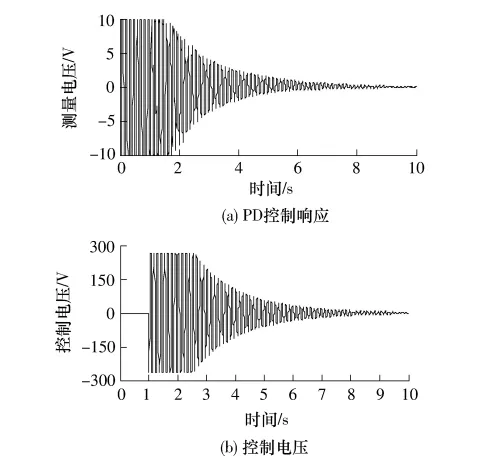
图8 第1阶扭转模态振动PD控制Fig．8 PD control of the vibration of the first torsional mode

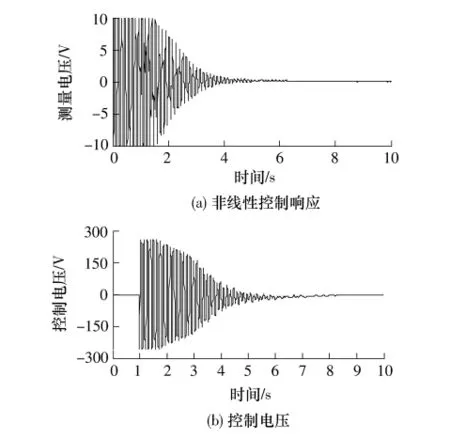
图9 第1阶扭转模态振动非线性控制Fig．9 Nonlinear control of the first order torsion mode vibration

6 结论

针对压电悬臂板结构进行了有限元建模、压电传感器/驱动器配置优化和振动主动控制研究．实验结果表明，设计的试验装置中采用压电传感器/驱动器优化配置方案，实现了对悬臂板弯曲和扭转模态在检测和驱动上的解耦;提出的非线性算法相较于PD算法可以更加有效地抑制压电悬臂板的弯曲和扭转模态振动，尤其是对小幅值振动的快速抑制．

［1］ 李东旭．挠性航天器结构动力学［M］．北京:科学出版社，2010．

［2］ 黄文虎，王心清，张景绘，等．航天柔性结构振动控制的若干新进展［J］．力学进展，1997，27(1):5-16．Huang Wen-hu，Wang Xin-qing，Zhang Jing-hui，et al．Some advances in the vibration control of aerospace flexible structures［J］．Advances in Mechanics，1997，27(1):5-16．

［3］ Lam K Y，Peng X Y，Liu G R，et al．A finite-element model for piezoelectric composite laminates［J］．Smart Materials and Structures，1997，6(5):583-591．

［4］ Chandrashekhara K，Bhatia K．Active buckling control of smart composite plates-finite-element analysis［J］．Smart Materials and Structures，1993，2(1):31-39．

［5］ Yasin M Y，Ahmad N，Alam M N．Finite element analysis of actively controlled smart plate with patched actuators and sensors［J］．Latin American Journal of Solids and Structures，2010，7(3):227-247．

［6］ Han J H，Lee I．Optimal placement of piezoelectric sensors and actuators for vibration control of a composite plate using genetic algorithms［J］．Smart Materials and Structures，1999，8(2):257-267．

［7］ 王威远，魏英杰，王聪，等．压电智能结构传感器/作动器位置优化研究［J］．宇航学报，2007，28(4):1025-1029．Wang Wei-yuan，Wei Ying-jie，Wang Cong，et al．Optimal investigation of senor/actuator placement for piezoelectric smartstructure［J］．Journal of Astronautics，2007，28(4):1025-1029．

［8］ Hiramoto K，Doki H，Obinata G．Optimal sensor/actuator placement for active vibration control using explicit solution of algebraic riccati equation ［J］．Journal of Sound and Vibration，2000，229(5):1057-1075．

［9］ Bruant I，Gallimard L，Nikoukar S．Optimal piezoelectric actuator and sensor location for active vibration control，using genetic algorithm ［J］．Journal of Sound and Vibration，2010，329(10):1615-1635．

［10］ 王军，杨亚东，张家应，等．面向结构振动控制的压电作动器优化配置研究［J］．航空学报，2012，33(3):494-500．Wang Jun，Yang Ya-dong，Zhang Jia-ying，et al．Investigation of piezoelectric actuator optimal configuration for structural vibration control［J］．Acta Aeronautica et Astronautica Sinica，2012，33(3):494-500．

［11］ Qiu Z C，Zhang X M，Wu H X，et al．Optimal placement and active vibration control for piezoelectric smart flexible cantilever plates［J］．Journal of Sound and Vibration，2007，301(3/4/5):521-543．

［12］ Philip S，Richer E，Hurmuzlu Y．Theoretical and experimental study of effcient control of vibration in a clamped square plate［J］．Journal of Sound and Vibration，2005，282(1/2):453-473．

［13］ Ma K．Adaptive non-linear control of a clamped rectangular plate with PZT patches［J］．Journal of Sound and Vibration，2003，264(4):835-850．

［14］ Lin J，Liu W Z．Experimental evaluation of a piezoelectric vibration absorber using a simplified fuzzy controller in a cantilever beam［J］．Journal of Sound and Vibration，2006，296(3):567-582．

［15］ Su C Y，Stepanenko Y．On the robust control of robot manipulators including actuator dynamics［J］．Journal of Robotic Systems，1996，13(1):1-10．

［16］ Seraji H．A new class of nonlinear PID controllers with robotic applications［J］．Journal of Robotic Systems，1998，15(3):161-181．