移动交通荷载下饱和沥青路面的水力耦合分析*

罗苏平 但汉成† 李亮 李凌

(1．中南大学土木工程学院，湖南 长沙410075;2．昆士兰大学土木工程学院，昆士兰布里斯班4072)

路面水损害是一种较为普遍的路面破坏现象．分析其原因可知，孔隙水压力和重载及其耦合作用是导致沥青路面水损害的主要因素．因此，积极开展路面水力－应力耦合情况下沥青路面力学行为的研究，对于全面了解路面破坏机理至关重要［1］．

为阐述水对路面破坏的机理，从而了解孔隙水压力的变化规律，近年来国内开展了一些相关的试验和理论方面的研究［2－4］．在国外，Khalili等［5］从不同角度、采用不同方法研究了动荷载和水的耦合作用下路面各种物理场的分布情况，也有学者采用理论分析和数值计算相结合的方法来探讨沥青路面内水分运移特征［6］．这些研究大都是基于路面荷载随时间的变化关系为某一函数(半正弦或折线)的假设，该假设虽然具有一定的合理性，但是与实际移动交通荷载有所区别。Cai等［7］提出了一个关于移动交通荷载作用下的饱和沥青路面动力响应物理模型，把饱和路面视为Kirchhoff薄板，上覆于半无限饱和的弹性多孔介质基础之上．尽管这具有一定的合理性，但是路面系统有其自身的特殊性:首先，路面本身是一个多层体系，逐层研究将更为合理;另外，将路面整体视为薄板，也无法得到板内的剪切应力分布情况．除此之外，一般可以将路面面层视为饱和多孔介质，基层很少处于饱和状态，而且路基也不是完全饱和．众所周知，在工程上设置相应的排水设施降低路基土的含水量的目的也是为了尽量保证路基土干燥或者具有低含水量．因此，进一步研究路面系统在移动交通荷载作用下的动力响应尤为重要．

文中建立一个二维三层体系的模型，包括面层、基层和路基(如图1所示)．路面面层视为饱和的弹性多孔介质，基层和路基视为干燥的弹性介质．通过求解耦合模型，对比分析干燥路面和饱和路面在应力分布和孔隙水压力分布方面的差异，并分析路面面层底部排水条件对路面动力响应的影响．

1 二维路面渗流模型假设和动态响应控制方程的建立

1．1 模型的建立

如图1所示，路面系统由均匀的弹性多孔介质面层(孔隙被水充满处于饱和状态，厚度为H1)、基层和路基组成．基层和路基均为干燥的弹性介质，厚度分别为 H2－H1、H3－H2．

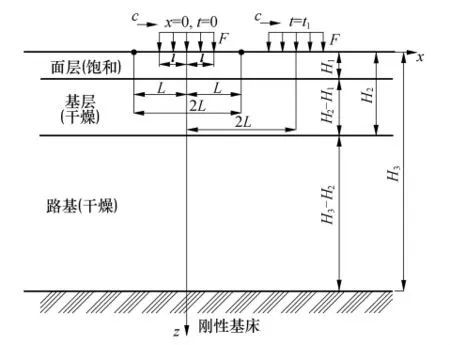
图1 路面在移动荷载作用下的示意图Fig．1 Schematic diagram of pavement under moving load

路基某深度处的位移可视为0．所有路面系统的结构层横向宽度假设为无限大，面层内的水与大气接触，在压力作用下可以自由溢出面层顶面．为便于建立数学模型，文中假设如下:

(1)路面各结构层为均质的各向同性弹性材料;

(2)尽管路面面层材料在荷载作用下产生形变，但渗透系数保持不变;

(3)达西定律仍然适用于描述液相的动量;

(4)忽略固相和液相的体积应力;

(5)各个结构层的层间位移和应力连续．

路面面层由沥青(粘结剂)和集料组成，具有连续的孔隙，孔隙中被水填充．液相运动的平均速度用v表示(vx和vz)，固相运动的平均速度用w表示(wx和wz)，两者的密度分别为ρf和ρs，孔隙率为n．

根据Biot动力固结理论，有如下的控制方程［8］:

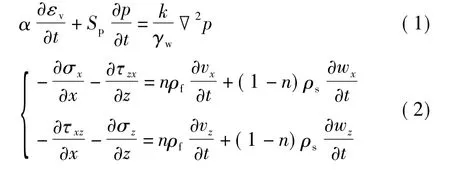
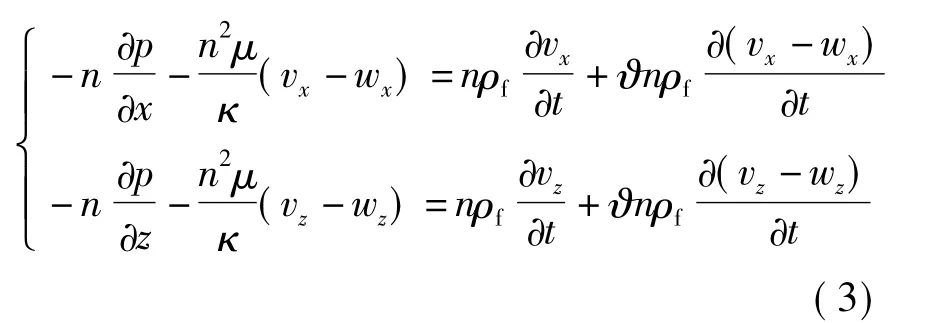
式(1)为基于质量守恒原理得到的连续性方程，式(2)为描述液相与固相共同作用的动量方程，式(3)为液相的动量方程．式(1)－(3)中:α为Biot固结系数，α=1－Cs/Cm，Cm为多孔介质的压缩系数(Pa－1)，Cs为固相材料的压缩系数(Pa－1)，Sp为孔隙的弹性释水系数(Pa－1)，可以表示为Sp=nCf+(α －n)Cs，Cf为液相(水)的压缩系数;εv为多孔介质的体积应变;k为多孔介质的渗透系数(m/s);σx和σz为固相在x、z方向上的正应力(Pa);zx为x-z平面的剪切应力(Pa);p为孔隙水压力(Pa);κ为多孔介质的渗透率(m2);ϑ为孔隙分布的曲率系数，表示由于渗流路径的弯曲而相对于直线渗流路径所增加的质量百分比;μ为孔隙水的动力粘滞系数(Pa·s);γw为水的容重(kg·m－2·s－2);t为时间坐标;▽2为Laplace算子．

根据文中模型采用的第3条假设，式(3)的右边可以退化为0，因此可以得到以下方程:

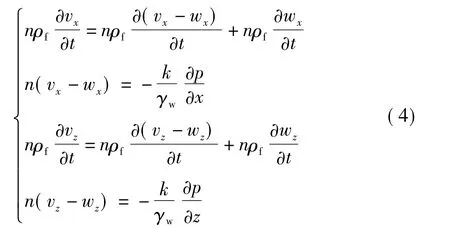
对于二维平面应变问题，基于Hooke应力应变原理以及材料的阻尼性质，控制方程(1)－(3)可以转化为如下形式:

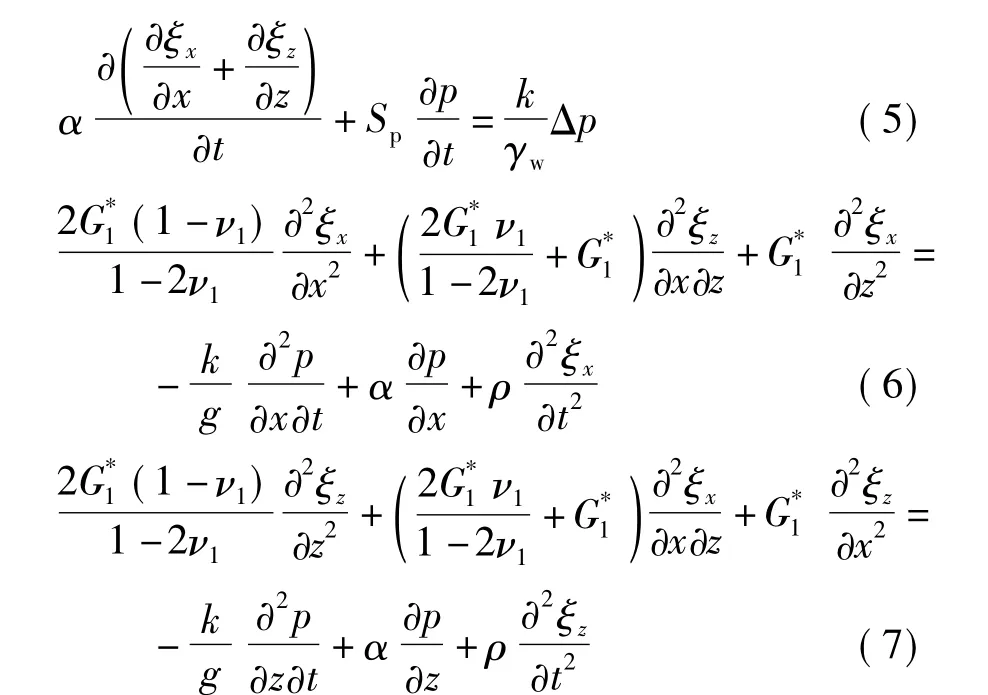
式中，ξx、ξz分别为 x、z方向的位移．

1．2 基层和路基模型的动态响应控制方程

根据对路面系统的描述，基层和路基被视为干燥的弹性介质，因此，可以采用动力平衡方程来描述，表示为

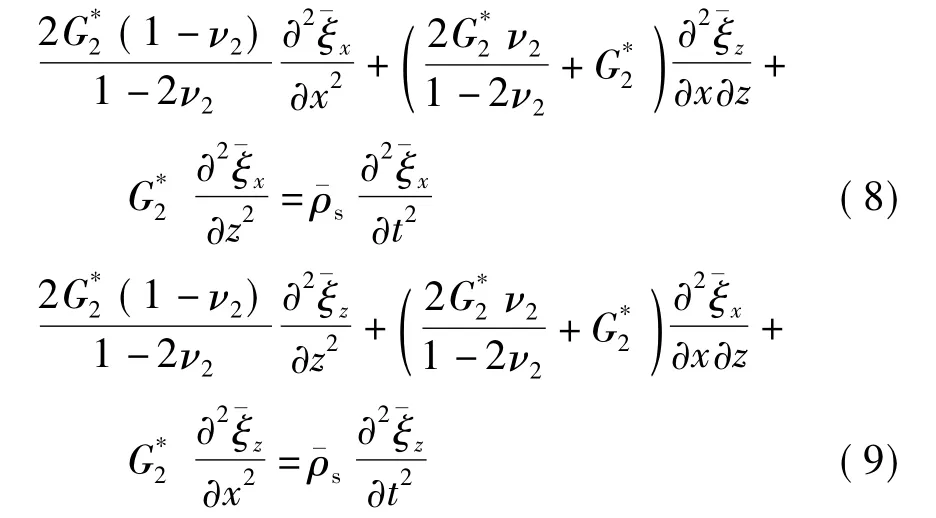
G*为复弹性剪切模量，可以表示为

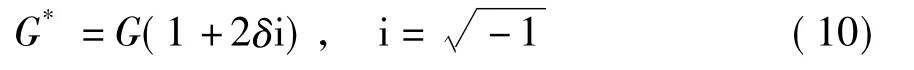
式中，δ为材料阻尼系数，G为固相在静止状态下的剪切模量．

二维情况下，可以将交通荷载简化为条形荷载．荷载宽度为2l，强度为F，以速度c移动．作用的荷载采用Fourier级数展开．某一点的动力响应在荷载通过该点之后会逐渐衰减直到下一次的荷载作用．假设从第一次荷载作用到下一次荷载作用的距离为2L［9］(如图1所示)，这个长度可以被视为两个交通荷载之间的距离．移动荷载函数(t=0)用Fourier级数可以表示如下［10-11］:

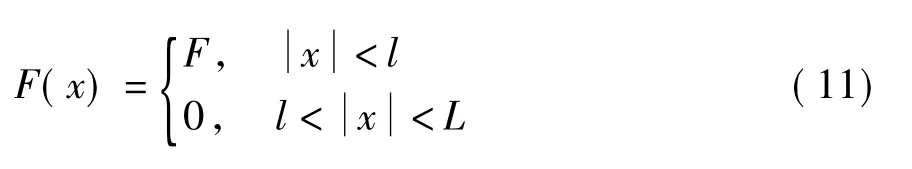
和

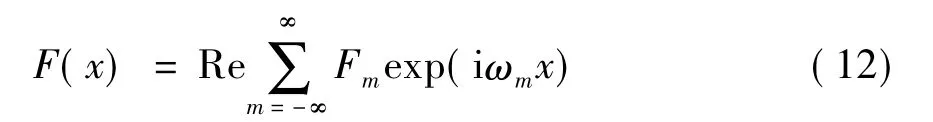
式中:ωm=2m/T，T为移动荷载的分布周期，文中设为2L;m为实数，范围为－∞到+∞．

如果采用移动坐标系统，即假设坐标系统以同样的速度沿荷载移动的方向移动，那么移动交通荷载在任意时刻的Fourier级数表达式为

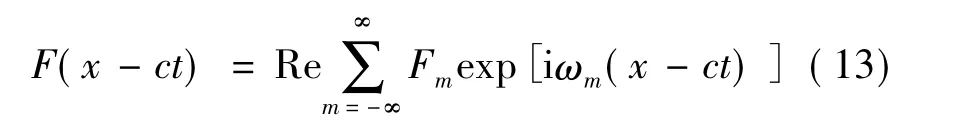
根据Fourier变换，Fm可以表示为

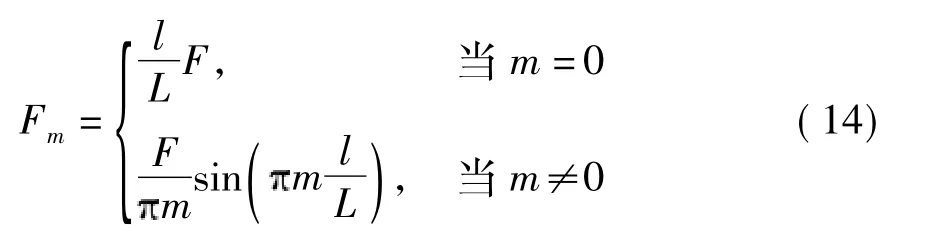
由于面层的性质是独立于坐标系统的(各向同性)，线性系统中的任何函数 φ(x，z，t)都可以表示为一组线性的谐函数的级数和［9］，其表示形式如下:

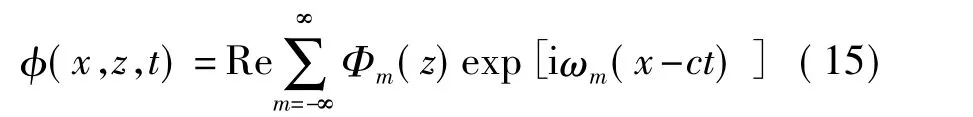
式中:Φm(z)仅为独立变量z的函数，Φm(z)=Φm为m次谐函数，指数函数部分仅为x－ct的函数．

根据式(15)，面层控制方程可以表示为

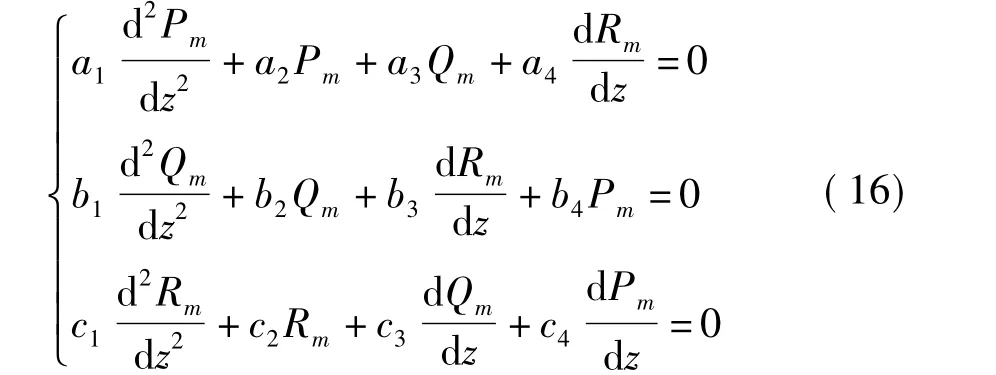
式中的参数表示为

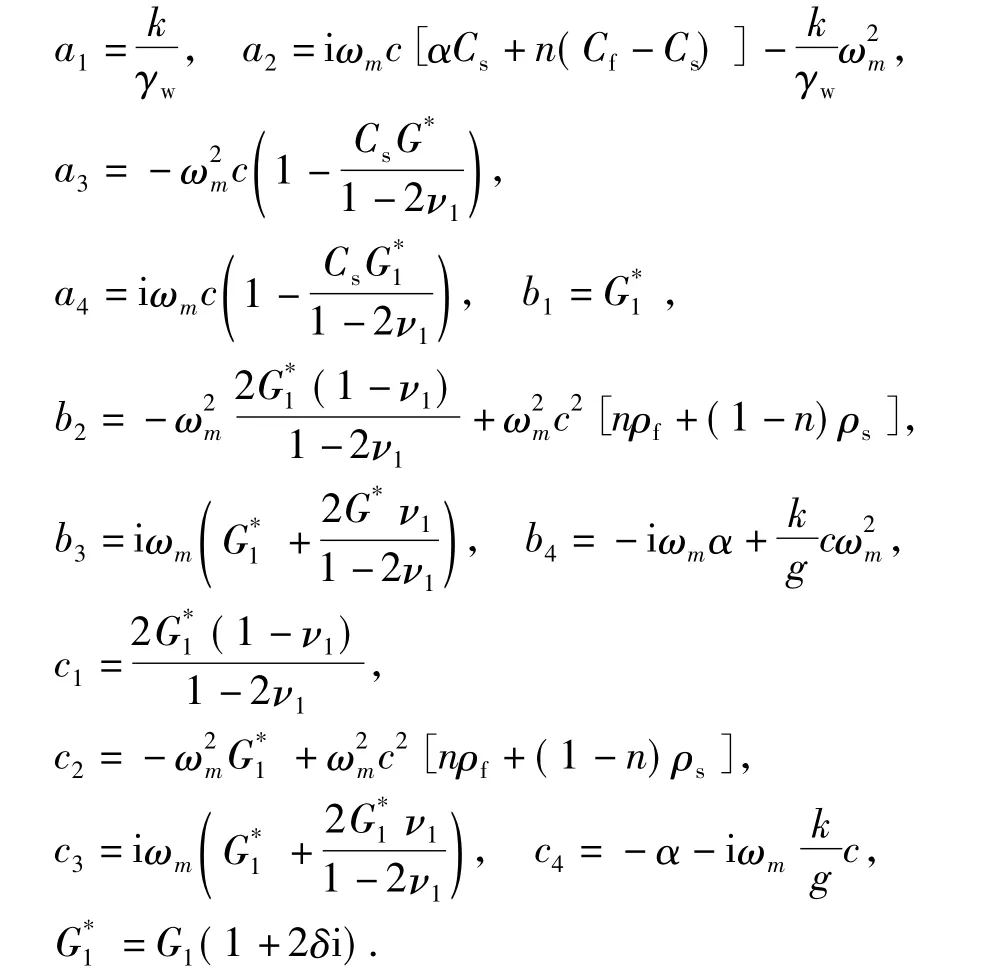
式中:G1为面层材料的剪切模量，Pa;ν1为面层材料泊松比;其他参数见前文所注．

因此，式(16)的通解可以表示为

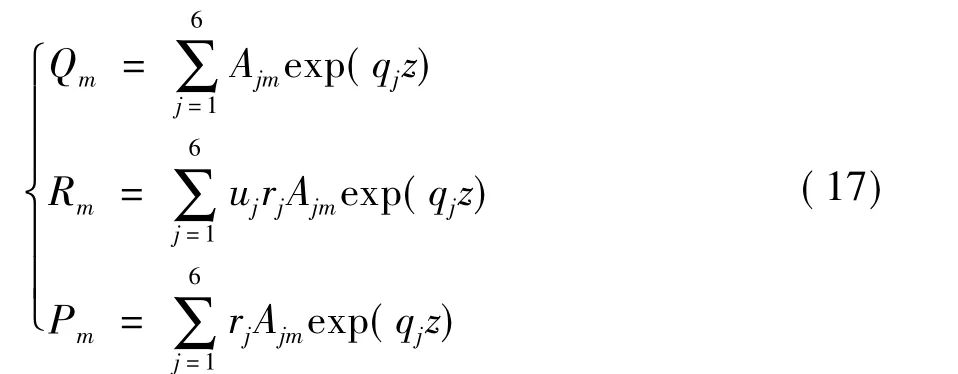
式中:Ajm为常数．

将式(17)代入到式(16)后简化得到

式中，

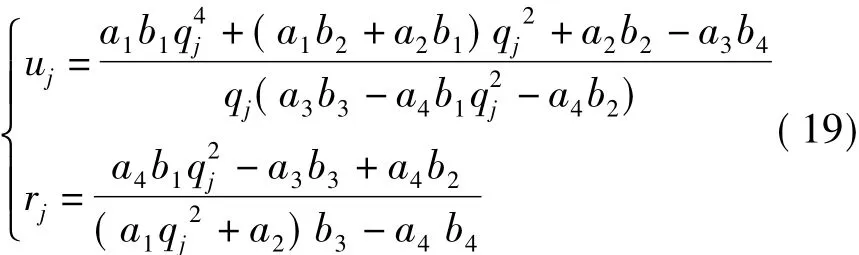
qj(j=1，2，…，6)为如下六阶多项式的根:

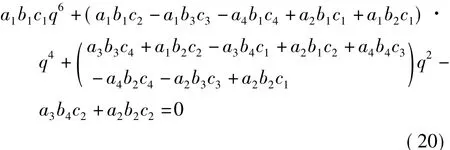
其根可以采用数值方法得到．

同样地，基层和路基的动力控制方程的解也可以采用以上方法得出．

1．3 边界条件

要求解控制方程，必须得到积分常数，如Ajm(j=1，2，…，6)等．由于轮胎与路面之间的摩擦为滚动摩擦，摩擦力大小的量级相对于交通荷载来讲是可以忽略的．因此，为了便于求解控制方程，轮胎与面层接触面的剪切应力可以设为零［9］．由此得到如下的边界条件:在面层顶面(z=0)，xz=0，σz=F 和p=0;在面层底部(z=H1)，位移边界条件ξx=δ1和ξz=δ2;在面层底部，与排水有关的边界条件分为两种类型，一种为不排水边界，另一种为完全排水边界(p=0)．另外，对于基层模型来讲，基于各层边界处位移和应力的连续性假设，可以得到一系列的边界条件．再者，在路基底部(z=H3)，位移假设为零．

1．4 控制方程的通解形式

通过数值方法(Matlab编程计算)可以得到位移、正应力和剪切应力．然后代入到路面系统在动载作用下的动力响应的控制方程的通解表达式(15)和(17)中，可以得到如下位移与孔隙水压力的表达式:

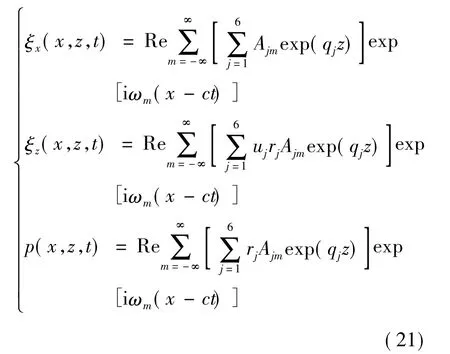
此外，路面面层内的孔隙水的流速、剪切应力与正应力的表达式可以分别根据Darcy定律和Hooke原理得出，限于篇幅，文中不再赘述．

2 数值计算与分析

2．1 模型验证

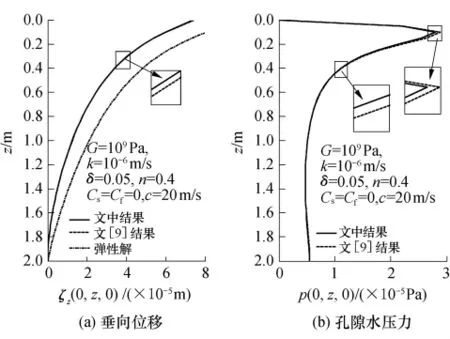
图2 文中计算的沿深度的垂向位移和孔隙水压力与文［9］计算结果的对比Fig．2 Vertical displacement and pore water pressure in depth direction of surface course respectively obtained by Ref．［9］and present work

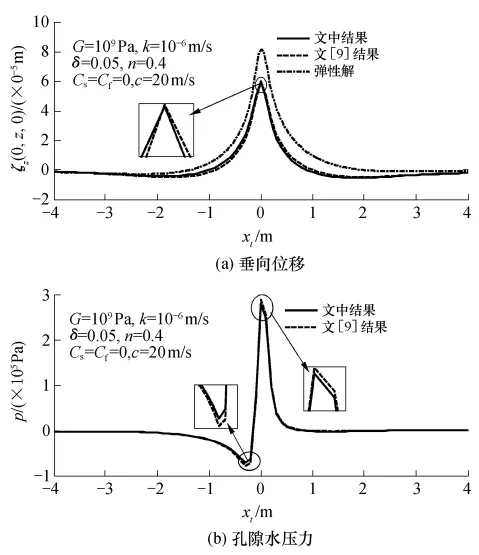
图3 文中计算的沿水平方向的垂向位移和孔隙水压力与文［9］计算结果的对比Fig．3 Vertical displacement and pore water pressure in horizontal direction of surface course respectively obtained by Ref．［9］and present work

图2和3对比了文中方法和文［9］的计算结果．荷载表达式为Fourier级数展开式，取4000个级数和来表示荷载，即荷载函数为4000个谐函数的级数和．F=700000 Pa(轮胎与路面的接触压力，标准轴载情况下为 0．7MPa［12］)，c=20m/s(荷载移动速度)，l=0．1m(轮胎与底面接触单宽为 0．2 m)，L=50m(荷载间距为100m)，H=2 m(饱和多孔介质的厚度，为单层多孔介质)，δ=5%(多孔介质材料阻尼系数)．沿深度方向(z为变量)将x=0、t=0处设为计算观察断面;沿水平方向(xt=x－ct为变量)，将z=0．1m处作为计算观察断面．文中采用了两种渗透系数(k=1×10－5m/s和1×10－6m/s)作计算对比．其他的计算参数列于表1与2中．H

表1 模型验证所采用的相关计算参数Table 1 Parameters with respect to model validation

—

表2 与交通荷载和路面材料有关的参数Table 2 Parameter with respect to traffic load and pavement material

图2与3中，ξz为垂向位移，p为孔隙水压力，z为深度，xt为横向位置．根据计算结果，从图2和3可看出，采用文中方法计算的垂向位移与孔隙水压力与文［9］的计算结果无论是沿深度方向上还是沿水平方向上都能较好地吻合．显然，饱和弹性多孔介质与干燥弹性介质两者在位移上的响应差异较为明显，并且干燥状态下具有更大的位移．其原因为:饱和多孔介质由于孔隙水压力的产生(孔隙水承担一部分荷载)导致多孔介质材料的有效应力降低，因此应变较小，位移也偏小．

文中用于计算分析的面层、基层和路基的参数取值列于表3中．主要研究对象为面层的位移、应力场、孔隙水压力场以及孔隙水的速度场．限于篇幅，文中暂不研究各个物理场随时间的变化(根据文中的计算方法，物理场随时间变化的关系很容易得到)，仅分析物理场沿深度方向上的分布情况．同时，将相关的物理场如位移场和应力场都与干燥面层条件下的工况做了相应的对比，如图4和5所示．

表3 k值对动力响应影响分析所采用的相关计算参数Table 3 Parameters for analyzing the effect of k on the dynamic response

2．2 饱和路面与干燥路面的动力耦合对比

为了测试孔隙水对面层应力状态的影响，文中对比了饱和路面和干燥路面在动荷载作用下的动力响应．计算参数为 k=10－8m/s、c=20m/s，其他参数的取值参照表2和3．图4为饱和路面与干燥路面的水平有效正应力的对比云图，颜色深浅代表有效正应力的大小，单位为Pa，等值线标于每张图上以便更清晰地理解应力大小与其分布，z表示深度，xt表示横向位置．可以明显地看出，在(－1，1)的区域内，干燥路面面层绝大部分是处于压缩状态(正应力值为压缩)，尤其在荷载作用区下方，应力在面层顶面处高度集中，最大值达到8．3×105Pa(该值从云图的计算数据中提取)．与干燥路面(图4(b))不同的是，饱和路面内部的应力分布有其自身的特点．在荷载作用区附近的(－1，1)区域的下方一定深度开始产生拉应力(图4(a))．除了在面层顶面荷载作用处的应力为压应力外，大面积的拉应力沿深度方向开展一直延伸到面层底部，最大的拉应力可以达到－1．42×105Pa(该值从云图的计算数据中提取)．因此，沿面层深度方向上，荷载作用区下方大部分面层包括底面都处于受拉状态．相对于干燥路面来说，饱和路面面层底部更容易产生拉应力，超过允许拉应力时会产生开裂．

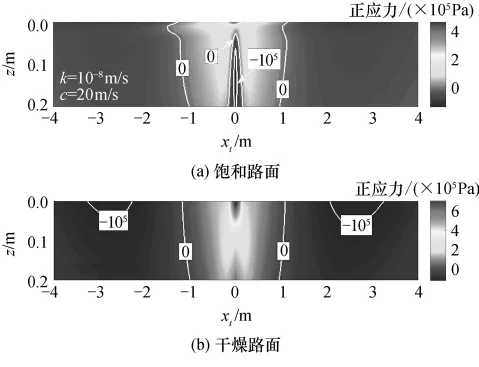
图4 饱和及干燥路面水平有效正应力的分布云图Fig．4 Comparison of horizontal effective normal stress contour between saturated and dry surface courses

此外，图5展示了这两种不同的路面状态的面层中垂向有效正应力的分布情况．从图5(b)中可以看到，在xt=0附近区域内形成了一条沿垂向分布的压应力带，而且在压应力带的两侧对称形成两“小片”拉应力区，但其最大值仅为－200Pa(该值从云图的计算数据中提取)．在图5(a)中，拉应力区的面积明显扩大，拉应力主要分布在沿面层水平方向的中间部分(xt=0)，最大拉应力大约为－1．61×105Pa(该值从云图的计算数据中提取)，且出现在面层顶面附近．除此之外，面层中大面积的出现拉应力也不利于层间粘结．

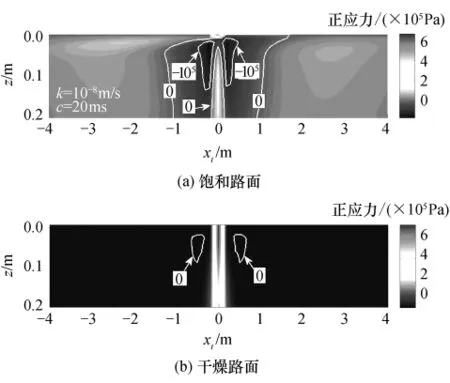
图5 饱和及干燥路面垂向有效正应力的分布云图Fig．5 Comparison of vertical effective normal stress contour between saturated and dry surface courses

2．3 边界排水条件的影响

从图6中可以看出，对于较大渗透系数的面层，排水边界条件下的孔隙水压力在整体上要小于不排水边界条件下的孔隙水压力．这是由于在这种情况下孔隙水承担的荷载比例较小，导致孔隙水压力相对较小而有效应力较大．在排水边界条件下，孔隙水压力在达到最大值后缓慢地减小到零压力，见图6．相对于不排水边界条件的情况，在面层渗透系数较大(k=10－6m/s)时，排水边界对孔隙水压力的影响是显著的．这种规律也可以从孔隙水流速场和垂直有效正应力场的对比得到反映，分别见图6(b)、6(c)和 7(a)．图 6(b)和 6(c)表明，在 k=10－6m/s的情况下，孔隙水流速相对于不排水边界情况下的流速更大，因为面层底面是完全排水的，孔隙水可以自由排出面层，而不排水边界条件下的孔隙水在面层底面区域会承压以至于被迫向两侧流动，从而导致垂向流速相对较小．

然而，对于渗透系数较小的路面(k=10－8m/s)，沿面层深度方向上的绝大部分区域，两种排水边界的各物理场的差异很小(见图6、7)，只是在面层底面区域有所差异，即在面层底面区域，具有排水边界的面层孔隙水压力在临近底面边界时快速降低至零压力，导致底面孔隙水流速有所增大．尽管排水边界的存在增大了孔隙水的流动速度，事实上孔隙水能通过排水边界自由地排出面层外，从而降低孔隙水压力，而且孔隙水排出之后，面层会转化为相对的非饱和态，这样非饱和面层内的孔隙水压力也会进一步降低(文中建立的模型没有涉及非饱和渗流)．

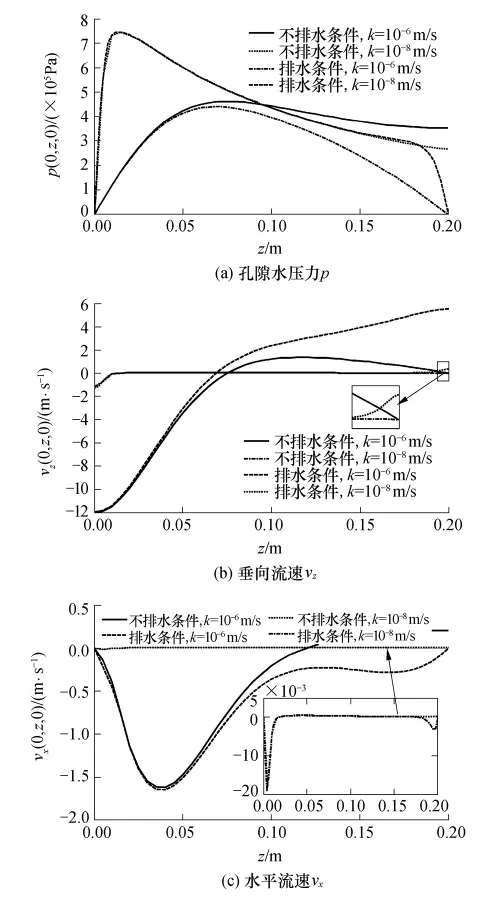
图6 孔隙水压力p、垂向流速vz、水平流速vx沿深度方向的分布Fig．6 Vertical distributions of pore water pressure p，vertical velocity vzand horizontal velocity vxin surface course

综上所述，排水条件对高渗透性面层各物理场的响应具有显著影响，而对低渗透性面层的影响较小，只是在接近面层底面区域影响较为显著．

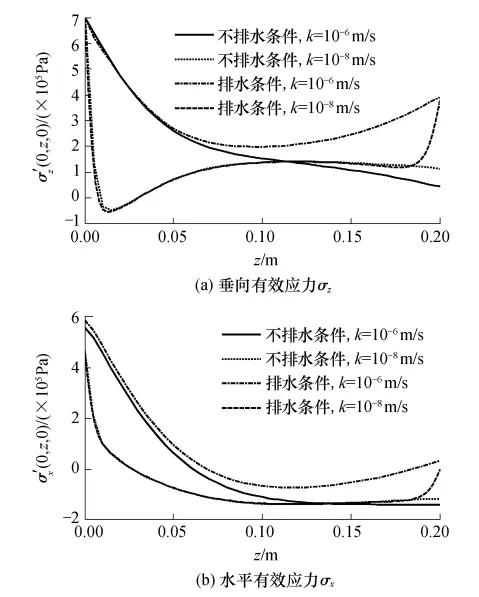
图7 垂向、水平有效应力σ'z和σ'x沿深度方向的分布Fig．7 Vertical distributions of vertical and horizontal effective normal stress σ'zand σ'x

2．4 固相剪切模量的影响

最大孔隙水压力随面层剪切模量和基层剪切模量的变化见图 8．计算参数为 k=10－6m/s，n=0．1和c=20m/s．可以看出，孔隙水压力最大值随着面层剪切模量(G1)的增大而有所降低，这是由于剪切模量小的面层比剪切模量大的面层承担的荷载比例小．例如在不排水边界条件下，当G1从4．80×108Pa增加到6．0 ×108Pa，G2=560MPa时，最大孔隙水压力从4．63×105Pa降低到1．24×105Pa，降低了73．2%;当在排水边界条件下，最大孔隙水压力很显著地从4．41 ×105Pa 降低到0．34 ×105Pa，降低了92．3%．从计算得到的结果，可以做进一步的推测，当路面温度升高时，由于沥青路面的模量会降低，这种降低的趋势随着深度增加而减小．在路面模量下降的同时，面层中的孔隙水压力会相应增加，会加速路面破坏．

另外，无论是在排水边界条件还是在不排水边界条件下，最大孔隙水压力都随着基层剪切模量(G2)的降低而有所增加．这是因为相对柔性的基层更容易被压缩，承担的荷载比例较小，相对多的荷载被路面面层承担，这样造成了面层中孔隙水压力的增大．这种增加的比例在不同的面层剪切模量情况下有所不同．例如，在不排水条件下，当面层的剪切模量(G1)为 4．8×108Pa时，基层剪切模量从5．6 ×108Pa减小到3．0 ×108Pa，最大孔隙水压力从4．63×105Pa增加到5．13×105Pa;而当面层的剪切模量(G1)为6．0×109Pa时，基层剪切模量从5．6×108Pa减小到3．0×108Pa，最大孔隙水压力从3．40×104Pa增加到3．51×104Pa．两种不同面层剪切模量情况下的增加比例分别为11%和4%．

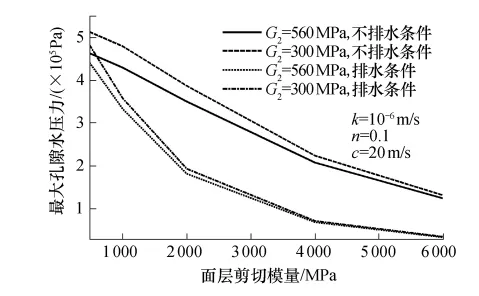
图8 最大孔隙水压力随面层剪切模量和基层剪切模量的变化Fig．8 Variation of maximum pore water pressure with shear moduli of surface course and base course

3 结论

(1)相对于干燥弹性的沥青路面，饱和沥青路面在移动交通荷载作用下会产生较高的拉应力，形成更大的拉应力区，拉应力自面层顶部贯穿于面层底面．

(2)饱和路面面层底部更容易产生拉应力，超过允许拉应力时会产生开裂，开裂之后路面裂缝反射至面层顶面致使路面裂缝贯通，导致路表雨水加速渗入路面结构内部，从而使路面水损害快速发生;除此之外，面层中大面积出现拉应力不利于层间粘结，拉应力超过面层允许粘结力，在面层之间产生错动，破坏路面整体强度．

(3)排水边界会显著影响高渗透性路面内的孔隙水压力和孔隙水流速．但是对于低渗透性的路面而言，排水边界对孔隙水压力和孔隙水流速的影响较弱，只在接近于面层底部的小区域范围内影响较显著．

(4)具有排水边界的面层中的孔隙水压力较小，孔隙水流速较大;而具有不排水边界的面层中的孔隙水压力较大，孔隙水流速较小．

(5)孔隙水压力最大值随着面层剪切模量的增大而有所降低．另外，无论是在排水边界条件还是在不排水边界条件下，最大孔隙水压力都随着基层剪切模量的降低而有所增加．

［1］ 薛强，盛谦．沥青路面破坏的多场耦合效应及控制技术［M］．北京:科学出版社，2009．

［2］ 傅搏峰，周志刚，陈晓鸿，等．沥青路面水损害疲劳破坏过程的数值模拟分析［J］．郑州大学学报:工学版，2006，27(1):51－58．Fu Bo－feng，Zhou Zhi－gang，Chen Xiao－hong，et al．The numerical simulation analysis of asphalt pavement moisture damage fatigue failure process［J］．Journal of Zhengzhou University:Engineering Science，2006，27(1):51－58．

［3］ 董泽蛟，谭忆秋，曹丽萍，等．水－荷载耦合作用下沥青路面孔隙水压力研究［J］．哈尔滨工业大学学报，2007，39(10):1614－1617．Dong Ze－jiao，Tan Yi－qiu，Cao Li－ping，et al．Research on pore pressure within asphalt pavement under the coupled moisture－loading action ［J］．Journal of Harbin Institute of Technology，2007，39(10):1614－1617．

［4］ 董泽蛟，曹丽萍，谭忆秋，等．表面排水条件对饱水沥青路面动力响应的影响分析［J］．公路交通科技，2008，25(1):10－15．Dong Ze－jiao，Cao Li－ping，Tan Yi－qiu，et al．Influence of surface drainage conditions on dynamic response of saturated asphalt pavement［J］．Journal of Highway and Transportation Research and Development，2008，25(1):10－15．

［5］ Khalili N，Selvadurai A P S．On the constitutive modelling of thermo－hydro－mechanical coupling in elastic media with double porosity［M］∥Ove S．Elsevier Geo－Engineering Book Series:Elsevier，2004:559－564．

［6］ Kettil P，Engstrom G，Wiberg N E．Coupled hydro－mechanical wave propagation in road structures［J］．Computers ＆ Structures，2005，83(21/22):1719－1729．

［7］ Cai Y Q，Cao Z G，Sun H L，et al．Dynamic response of pavements on poroelastic half－space soil medium to a moving traffic load ［J］．Computers and Geotechnics，2009，36(1/2):52－60．

［8］ Verruijt A．An introduction to soil dynamics［M］．Berlin:Springer，2010．

［9］ Theodorakopoulos D D．Dynamic analysis of a poroelastic half－plane soil medium under moving loads［J］．Soil Dynamics and Earthquake Engineering，2003，23(7):521－533．

［10］ Siddharthan R，Zafir Z，Norris G M．Moving load response of layered soil．Ⅰ:formulation［J］．Journal of Engineering Mechanics－Asce，1993，119(10):2052－2071．

［11］ Siddharthan R，Zafir Z，Norris G M．Moving load response of layered soil．Ⅱ:verification and application［J］．Journal of Engineering Mechanics－Asce，1993，119(10):2072－2089．

［12］ TG D50—2006，公路沥青路面设计规范［S］．