进出口道综合效率最优的交叉口配时参数优化方法

马东方，王殿海, ，宋现敏，金盛

(1. 吉林大学 交通学院，吉林 长春，130022；2. 浙江大学 建筑工程学院，浙江 杭州，310058)

交通拥堵已成为制约世界各大城市可持续发展的普遍问题，如何在给定的城市路网条件下，采用先进的交通管理与控制措施提高路网交通流的运行效率是当今世界的热点话题。信号控制作为城市交通管理与控制的基本手段之一，其目标是将冲突交通流在时间和空间上进行分离，以保证交通流的运行效率和安全性。单点控制是一种最为基本的信号控制方式，主要控制参数包括周期时长和相位绿信比，其中周期时长是一战略控制参数，而绿信比属于战术控制参数[1]，二者共同决定着交叉口信号控制的效果。针对单点定周期控制下的信号交叉口，常用的配时参数优化方法有：TRRL法、ARRB法、HCM法[2-3]以及基于智能算法的优化方法[4-6]，但这些方法仅适用于进口道流量较低的情况，对过饱和情况考虑不足。近年来，随着城市交通拥堵问题的日益加剧，越来越多交叉口的交通流运行经常处于过饱和状态，已经成为城市路网交通流运行效率的严重“瓶颈”。为此，一些科研工作者对适应于过饱和情况的配时参数优化方法展开了研究，代表性成果有：Chang等[7]提出的以整个过饱和时段为优化间隔、以 PI(综合排队长度和车辆延误 2个指标)值最小为优化目标的动态优化方法；Papageorgiou等[8]以优化时段内控制区域所有路段的排队长度之和最小为优化目标，提出了一种相位绿灯时长及相位差的优化方法；Liu等[9]在考虑干道排队长度演化及车道组间交通流的相互影响下，建立了一种过饱和情况下的信号参数优化方法。然而，上述3种方法仅以交叉口所有关键进口道的车均延误或其他综合指标值最优为优化目标，并没有考虑交叉口出口道限制对信号参数优化的影响。在我国实际的城市路网中，部分城市存在着为数众多的短连线路段，本文称其为“瓶颈”路段。高峰时段内，由于下游交叉口的通行能力与上游交叉口单位时间内驶入该路段的车辆数存在一定偏差，短路段处经常发生排队上溯现象，产生“多米诺”效应，造成局部、甚至是整个路网的交通拥堵[10]。因此，仅以进口路段的车辆到达率为决策变量、以车均延误最小或其他综合指标最优为优化目标得到的配时参数，未能全面考虑进口车道和出口车道通行能力的匹配问题，在工程应用中受到一定程度的限制，尤其是在进、出口存在“瓶颈”路段的交叉口。本文作者以单点分时段控制的信号交叉口为研究对象，以交叉口的控制方式、输入路段的车辆到达率、输出路段的下游通行能力及路段长度等因素为输入变量，提出了一种以控制时段内交叉口所有进口路段和出口路段的周期平均车辆数之和最小为优化目标的配时参数优化方法，并进行相应的算法实例分析。

1 优化思想

为满足定周期控制交叉口不同时段的交通需求，配时参数应以一定的时段 T为优化间隔进行实时优化。以交叉口的所有进口路段及出口路段为整体进行考虑时，为了尽量提升交叉口的时空资源利用效率、降低过饱和现象出现的风险、防止路段排队上溯现象的发生，提出如下单点配时参数优化目标：T时间段内，交叉口中所有进口路段及出口路段的周期平均车辆数之和最小。

假设配时参数优化的时间间隔T为K个周期时长C，即T=KC，则针对某一进(出)口路段i，K周期内的路段平均车辆数为：

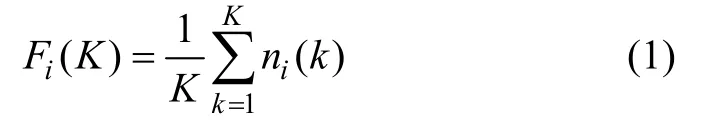
其中：Fi(K)为K个周期内路段i的周期平均车辆数；ni(k)为第k周期开始时刻路段i的容纳车辆数；k为优化时段内的周期编号，k=1，2，…，K，K∈N+；i为交叉口的进口路段及出口路段编号，取值为1，2，…，I；I为交叉口进出口路段数和出口路段数之和，I∈N+。

Fi(K)对所有进、出口路段累加求和，即为时段T内交叉口所有进口路段及出口路段的周期平均车辆数之和，其值为：

其中：F(K)为K个周期内交叉口进口路段和出口路段的周期平均车辆数之和；Iio为交叉口所有进、出口路段的集合。

为实现优化时段内交叉口所有进、出口路段的周期平均车辆数之和最小，F(K)应满足如下约束：

显然，ni(k)由交叉口的信号配时参数、车辆到达率及路段i的一些静态属性决定，是确定目标函数的关键。

2 配时参数优化模型

2.1 信号交叉口微观描述

交叉口是由一系列连接上下游节点的路段组成，按照路段交通流对交叉口作用性质的不同，可将路段划分为输入路段和输出路段2类[11]。如图1所示的信号交叉口共包含8条路段，其中1，2，3，4为输入路段，5，6，7，8为输出路段，可分别用 Iio，Iin，Iout代表交叉口所有路段、输入路段和输出路段的集合。在车辆到达率一定的前提下，输入路段的容纳能力决定着本路段所对应相位的最大输入量；在下游交叉口通行能力一定的前提下，输出路段的容纳能力决定着交叉口输入车流的最大输出量[12]。

路段容纳车辆数和单位时间内由进口路段驶入出口路段的车辆数是交叉口运行效率的直观表现，且二者均可表示为周期时长和绿信比的函数。受上下游信号控制的影响下，路段 i(i=1，2，…，8)的交通流运行如图2所示。

图1 交叉口路段结构图Fig.1 Example of one signal intersection comprising junctions

图2 路段交通流示意图Fig.2 Traffic flow schematization on link i

图2中，Sh,i(k)为k周期上游交叉口的h进口驶入路段i的车辆数；ui(k)为k周期上游交叉口驶入路段i的总车辆数；yi(k)为k周期驶离路段i的车辆数；Si,j(k)为k周期由进口路段 i驶入出口路段 j的车辆数；Ni为路段i的最大容纳车辆数。

由图2可知：上游交叉口驶入的车辆数、路段容纳车辆数与本路段驶出车辆数之间存在着相互影响、相互制约的关系，且由三者之间的关系可推导出进口路段和出口路段上的实时车辆数，为分析交叉口整体运行特征提供前提和基础。

2.2 路段实时车辆数计算

图 2中，针对交叉口的某一进(出)口路段 i，k+1周期开始时刻路段所容纳的车辆数受k周期开始时刻路段容纳的车辆数、k周期内驶入路段的车辆数及本周期内驶离路段的车辆数3个因素的影响，表达式为：

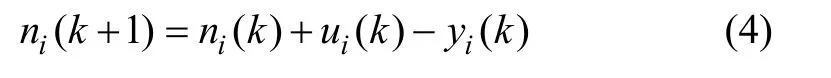
假设交叉口的I条进出口路段中包含W条输入路段，即：i=1，2，…，W表示输入路段；i=W+1，…，I表示输出路段。针对某进口路段i，若在配时参数优化时段内的路段车辆到达率为qi，则k周期f相位由上游交叉口驶入路段 i的车辆数 uif(k)应为本相位时间内理论到达的车辆数与路段最大剩余容纳能力的较小值，即：

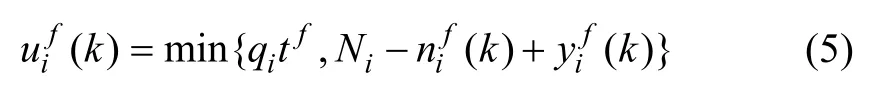
其中：qi为进口路段i的车辆到达率；tf为f相位的绿灯时长；为k周期f相位驶离路段i的车辆数；为k周期f相位开始时刻路段i的容纳车辆数。针对所有进口路段及出口道路段，按照相位顺序的不同， nif(k)均可用下式计算：

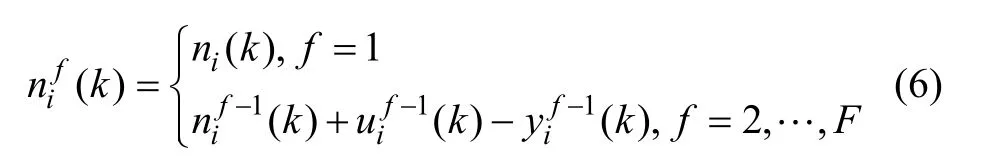
其中：F为信号控制相位数，F∈N+。

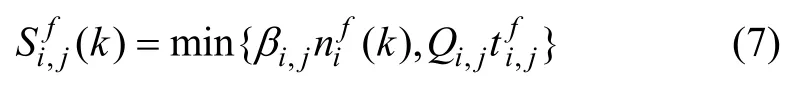
若相位绿灯时长大于车辆以自由流速度通过下游路段的时间，则本相位释放的部分车辆可直接驶离下游路段。针对某出口路段j，k周期f相位由上游节点驶入且本相位时间内能够直接驶离路段j的最大车辆数为：

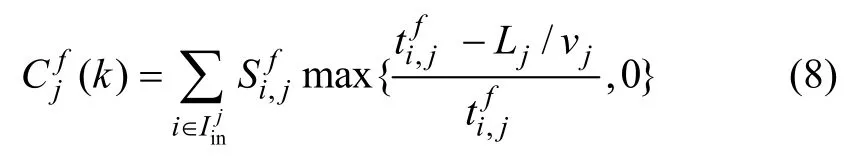
其中：Lj为j的路段长度，m；vj为车辆在路段j上的自由流速度，m/s；为与路段 j相关联的所有进口路段的集合。

在不考虑下游通行能力限制时，k周期f相位驶离路段j的最大车辆数为：

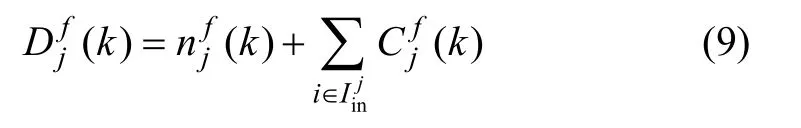
k周期f相位驶离路段j的实际车辆数应为本周期f相位驶离路段j的最大车辆数与下游交叉口中路段j所对应进口道f相位通行能力的较小值，即：

其中：Qj为下游交叉口中路段j所对应进口道的通行能力。

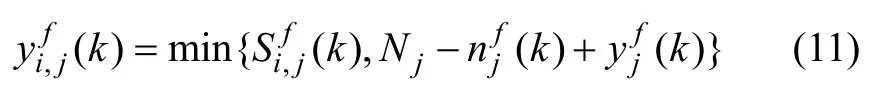
k周期内，由进口路段i驶入至所有出口路段j的车辆数之和，即为路段i在k周期驶出的总车辆数；而驶离输出路段j的车辆数为所有相位驶离的车辆数之和，表达式分别为：

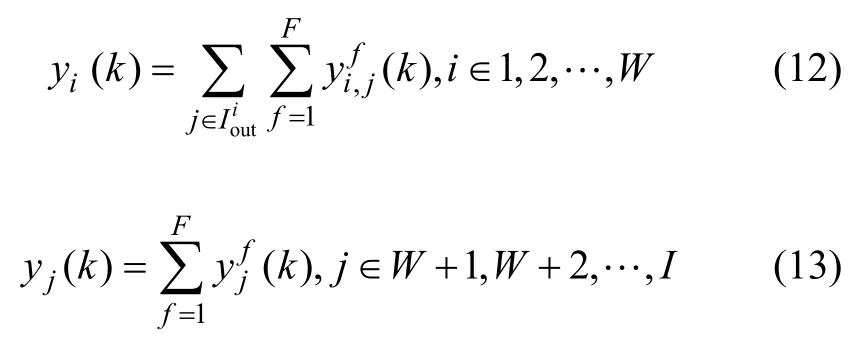
对于交叉口的输出路段，即当j=W+1，…，I时，k周期f相位能够驶入路段j的车辆数应为相位绿灯时间内上游交叉口所有进口道能够驶入的车辆数之和与路段j的剩余容纳能力的较小值，表达式为：

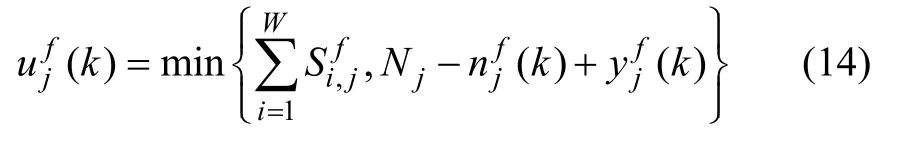
因此，k周期内进口路段及出口路段的驶入车辆数分别为：

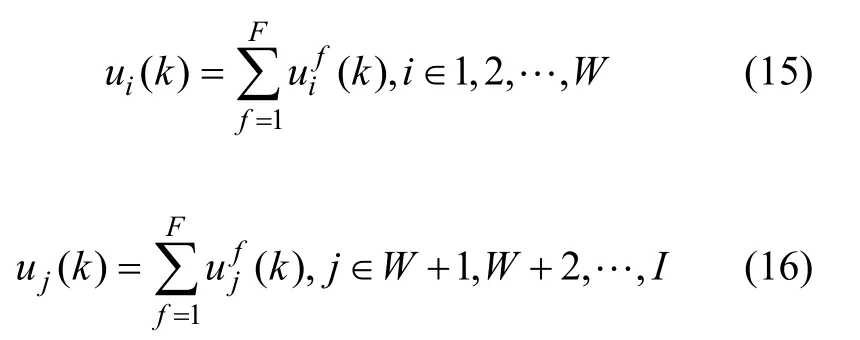
2.3 周期时长确定

将方程(4)～(14)代入到目标函数式(3)中，本文的配时参数优化过程即为求解如下数学优化问题：

满足：

考虑行人过街的安全性及驾驶员容忍极限时间等因素的限制，交叉口的相位绿灯时长应满足如下约束：

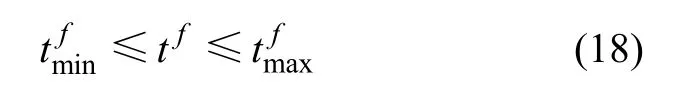
所有相位的绿灯时长及绿灯间隔时间之和即为交叉口的周期时长，表达式为：

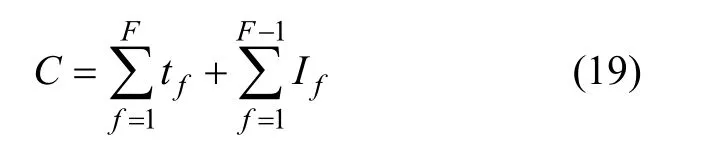
其中：C为交叉口周期时长，s；If为相位f与下一相位的绿灯间隔时间，s。

实际应用中，检测器应能准确检测得到优化间隔T内输入路段的流量数据。式(17)所示的数学规划问题即是寻求在特定的约束条件下使得目标函数值最小的tf值，且优化得到的周期时长及相位绿灯时长可作为下一时间间隔内配时参数的重要理论参考。

由于路段实时容纳车辆数、相位绿灯时间等参数的取值均为正整数，式(17)中的约束条件具有很强的不连续、不可微和高度非线性，采用传统的数值优化方法求解存在诸多问题。而遗传算法仅利用适用值信息、对目标函数和约束函数没有可导性的要求，具有简单、通用性强等优点，能够求解式(17)所示的数学规划问题；此外，遗传算法利用生物进化论思想，采用概率转移机制搜索可行性解空间，能够克服传统优化方法单点搜索的缺点。基于上述分析，本文采用遗传算法求解式(17)的数学问题。

3 实例分析

3.1 算例设计

为验证上述方法的有效性，本文以如图1所示的十字交叉口为例进行过饱和和低饱和情况下的实例分析。假设4个进口道均为直行单车道，交叉口采用两相位控制，且在过饱和情况下，4个进口道的车辆(以标准交通车计)到达率分别为0.3，0.2，0.2，0.25 辆/s;低饱和情况下进口道的车辆到达率分别为0.15，0.1，0.1，0.125 辆/s；此外，4个出口道通行能力分别为0.3，0.25，0.25，0.20 辆/s，低饱和状态下路段初始容纳车辆数均为10辆，过饱和状态下路段初始容纳车辆数为50辆，8条进口路段及出口路段的最大容纳能力及路段长度如表1所示。

表1 进出口路段1～8最大容纳能力及路段长度Table 1 Capacity and link length for 1-8 approaches

本文以10个信号周期为优化时间间隔，假设所有路段的自由流速度均为14 m/s，结合上述输入参量，通过遗传算法求解节点的配时参数值。

3.2 算例求解

遗传算法(Genetic Algorithm)是依据适者生存、优胜劣汰的进化原则对包含可能解的群体反复进行遗传操作，寻求最优或近似最优解的随机搜索算法，已被广泛应用于数学优化、自动控制、图像处理与模式识别等方面，主要内容包括编码、初始种群产生、适应度计算及遗传操作4个部分。

(1) 编码。由于行人过街时间及排队容忍时间等条件的制约，相位绿灯时长应有最大绿和最小绿限制，且二者的取值一般分别为60 s[13]和15 s[14]。设定本文的求解精度为整数，由于区间长度为 45，区间[15，60]必须分成45等份，因此编码的二进制串长至少需要6位。

(2) 种群产生。种群规模设定为50，初始种群的染色体随机选取。

(3) 适用度计算。考虑本文目标函数在定义域内的取值均大于 0，而且是寻找函数最小值，所以可直接引用目标函数的相反数作为适用度函数来评价染色体的优劣。即：

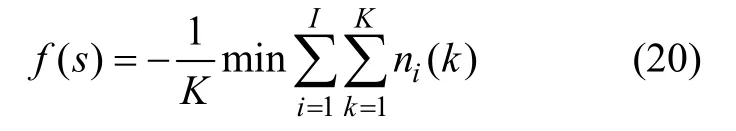
(4) 遗传操作。采用跨代精英选择机制，设定交叉概率pc=0.25，变异概率pm=0.01，交叉变异后形成的中间种群与父代种群合并后按照适应度进行排序，且50%个体形成下一代种群。

按照上述基本遗传算法，设定南北直行为第一相位，东西直行为第二相位，在满足 3.1节所设定的 2种交通状况下，式(17)的最优解分别为：过饱和状态下，t1=59 s，t2=60 s，优化目标函数值为581辆；低饱和状态下，t1′=48 s，t2′=18 s，优化目标函数值为 89辆。进口路段及出口路段的周期平均车辆数之和与相位有效绿灯时长的关系分别如图3和4所示。

假设所有相位的绿灯间隔时间均为3 s，2种状态下的交叉口的周期时长为：

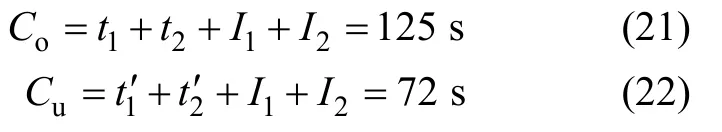
式中，Co为过饱和情况下的周期时长，s；Cu为低饱和状态下的周期时长，s。

通过上述算例分析可知，本文提出的单点配时参数优化算法可同时适用于低饱和及过饱和状态，且过饱和状态下的交叉口各相位绿灯时长均接近最大绿；低饱和状态下，虽然相位2的关键车流与相位1的关键车流车辆到达率近似相等，但出口路段 7属于“瓶颈”路段(路段长度为350 m，远小于其他路段的长度)，为避免路段排队长度的可能上溯，配时参数优化结果中的′远大于

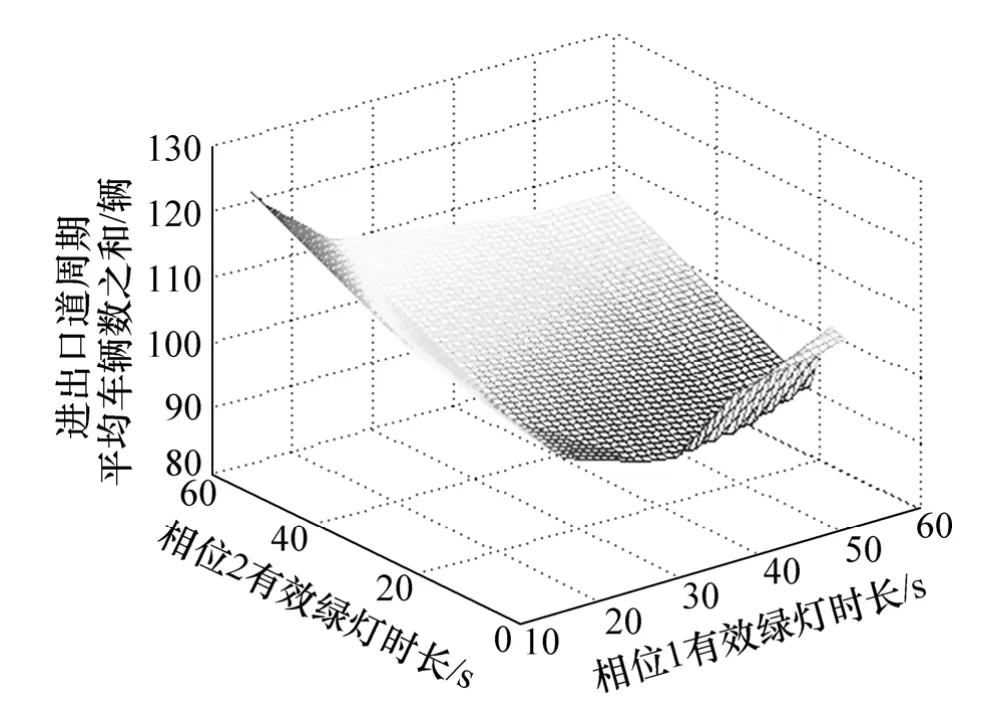
图3 低饱和状况下优化指标与相位绿灯时长关系Fig.3 Relationship between optimization index and phase green time with high saturation condition

图4 过饱和状况下优化指标与相位绿灯时长关系Fig.4 Relationship between optimization index and phase green time with low saturation condition

4 结论

(1) 针对经典的单点信号控制参数优化方法仅以关键进口车道的车均延误或其他综合指标最优为优化目标的局限，提出了以优化时段内交叉口所有进口路段和出口路段的周期平均车辆数之和最小为控制目标的优化思想；分析了路段车辆数的演化过程，推导了路段实时容纳车辆数的计算模型，在此基础上建立了基于进、出口道综合效率最优的配时参数优化方法，并通过遗传算法求解了具体算例，说明了本文方法的实用性。

(2) 路段实时车辆数还受到路段进出口的车辆汇入、行人及非机动车等其他因素的影响，复杂情况下的信号控制参数综合优化方法有待进一步研究。

[1]Diakaki C, Papageorgiou M, Aboudolas K. A multi-variable regulator approach to traffic-responsive network-wide signal control[J]. Control Engineering Practice, 2002, 10(2): 183-195.

[2]May A D. Traffic flow theory-the traffic engineer’s challenge[M]. Washington D C: Institute Traffic Engineers,1965: 290-303.

[3]顾怀中, 王炜. 交叉口交通信号配时模拟退火全局收敛算法[J]. 东南大学学报, 1998, 28(3): 68-72.GU Huai-zhong, WANG Wei. A global optimization simulated annealing algorithm for intersection signal timing[J]. Journal of Southeast University, 1998, 28(3): 68-72.

[4]Wong C K, Wong S C. Lane-based optimization of signal timings for isolated junctions[J]. Transportation Research Part B,2003, 37: 63-84.

[5]田丰, 边婷婷. 基于自适应遗传算法的交通信号配时优化[J].计算机仿真, 2010, 27(6): 305-308.TIAN Feng, BIAN Ting-ting. Traffic signal timing optimization based on adaptive genetic algorithm[J]. Computer Simulation,2010, 27(6): 305-308.

[6]肖业伟, 黄辉先, 王宸昊. 基于蚁群算法的交叉路口多相位信号配时优化[J]. 计算机工程与应用, 2008, 44(19): 241-244.XIAO Ye-wei, HUANG Hui-xian, WANG Chen-hao. Multiphase traffic signal timing optimization of intersection based on ant colony algorithm[J]. Computer Engineering and Applications,2008, 44(19): 241-244.

[7]Chang T H, Sun G Y. Modeling and optimization of an oversaturated signalized network[J]. Transportation Research Part B, 2004, 38: 687-707.

[8]Papageorgiou M, Diakaki C, Dinopoulou V, et al. Review of road traffic control strategies[J]. Proceedings of the IEEE, 2003,91(12): 2043-2067.

[9]LIU Y, Chang G L. An arterial signal optimization model for intersections experiencing queue spillback and lane blockage[J].Transportation Research Part C, 2010, 18: 130-144.

[10]Wu X K, Liu H X, Gettman D. Identification of oversaturated intersections using high-resolution traffic signal data[J]Transportation Research Part C, 2011, 19: 626-638.

[11]Mariagrazia D, Maria P F, Carlo M. A signal timing plan formulation for urban traffic control[J]. Control Engineering Practice, 2006, 14: 1297-1311.

[12]Barisone A, Giglio D, Minciardi R, et al. A Macroscopic Traffic model for real time optimization of signalized urban areas[C]//The 41st IEEE Conference on Decision and Control,Las Vegas, 2002: 900-903.

[13]张卫华, 陆化普, 石琴, 等. 公交优先的信号交叉口配时优化方法[J]. 交通运输工程学报, 2004, 4(3): 49-53.ZHANG Wei-hua, LU Hua-pu, SHI Qin, et al. Optimal signal-planning method of intersections based on bus priority[J].Journal of Traffic and Transportation Engineering, 2004, 4(3):49-53.

[14]LI Xiu-gang, LI Guo-qiang, PANG Su-seng, et al. Signal timing of intersections using integrated optimization of traffic quality,emissions and fuel consumption: A note[J]. Transportation Research Part D, 2004, 9(5): 401-407.