深锥浓密机搅拌刮泥耙扭矩力学模型

吴爱祥，焦华喆，王洪江，杨盛凯，姚高辉，刘晓辉

(北京科技大学 土木与环境工程学院，北京，100083)

作为固液分离的主要设备之一，浓密机在冶金、材料、矿业、造纸等各个行业得到应用[1-2]。但已有的研究主要集中在脱水机理、处理能力等方面，对于搅拌刮泥耙功率，目前最常用的方法是基于尾砂附着的厚度、尾砂与机体间的摩擦因数和耙子运动速度确定刮泥功率[3]。该方法假设浓密机搅拌耙区域内料浆均匀分布，且浓度(以固体质量分数计)在65%～70%的范围内。在浓度大于75%且分布不均匀的情况下，对于耙子运动受力的影响未能细化分析，特别是在极端状态下浓密机过载停机现象未进行研究[4]。某矿使用的新型深锥浓密机，能将质量分数为18%～30%的选厂全尾砂浆直接脱水浓缩，形成质量分数为76%～78%的底流，脱水效果较好。由于尾砂在深锥内部堆积，发生了深锥搅拌刮泥耙过载停机的事故，且发生的频率最高时达到4次/月，每次压耙的处理时间为16 h左右，极大地影响了正常生产[5]。假设深锥内部充满质量分数为70%以上的尾砂浆，通过分析不同位置、不同性质尾砂群对耙子运动的影响，对耙子的运动进行受力分析，计算耙子受力的极大值，建立耙子运动时的扭矩方程，最终得出搅拌刮泥耙最大扭矩的计算模型，并在此基础上对设备参数进行验算。

1 搅拌刮泥耙扭矩模型建立

1.1 深锥搅拌刮泥耙结构

耙式结构由水平支撑横梁和刮泥耙组成，在传动轴和横梁之间安装脱水杆。耙齿安装于耙臂上，将尾矿向机体中部收集，如图1所示。

图1 深锥浓密机内部料浆分布Fig.1 Slurry distribution in deep-cone thickener

耙子的传动机构的工作性能为：速度0.176 r/min，持续工作扭矩650.200 0 kN·m。传动机构配有扭矩传感器，当达到满扭矩的80%时，耙子停机保护。

1.2 浓密机内部料浆分布特征

浓密机耙子过载停机的事故处理过程中发现，锥部的机壁上附着了一层浓度极高，类似滤饼的附面层，用0.5 MPa的高压水都很难将其清洗干净。分析认为，搅拌刮泥耙与锥部机壁之间有一定的间隙，随着运行时间的延长，耙子不仅无法将颗粒全部刮掉，相反由于耙子的扰动，尾砂脱水更为充分，料浆质量分数能够达到85%～90%，形成了极难清洗的附面层。

鉴于上述工程实际，可认为浓密机内部料浆的分布划分为两大区域，流体区和散体区(非流体区)。在以往的研究中，普遍认为浓密机内部存在 4个区[6]，如图 1(a)所示，4个区均属于流体区，区内料浆质量分数一般低于80%，局部可达到82%，物料可以通过排料排出。散体区指该附面层区域，排料和刮泥均无法将该区域内物料清除。根据现场观测，该层的厚度完全覆盖了刮泥耙，耙子的运动对尾砂产生剪切作用。

1.3 搅拌刮泥耙受力分析

搅拌刮泥耙包括 3个部分，而支架(A)，立柱(B)和刮泥耙(C)，如图1(b)所示。支架和立柱2部分的运动区域中，尾砂浆浓度较低，按流体进行分析；刮泥耙距离帮壁较近，该处附着的矿泥含水量在塑限附近，物料阻力按散体分析。

根据 Wu[7]在静态和动态 2种情况下进行的含水率对散体抗剪强度的研究，认为随着水分的增加，抗剪强度先下降而后上升，水分含量wc在10%左右时，剪切应力τ出现峰值；而当含水量高于15%时，固液混合介质具有较好的流动性，抗剪强度很小，利用流变学方法描述抗剪强度更为合理。

1.3.1 支架受力分析

支架与驱动轴相连，转动时的运动轨迹为一圆柱体，如图2(a)所示。

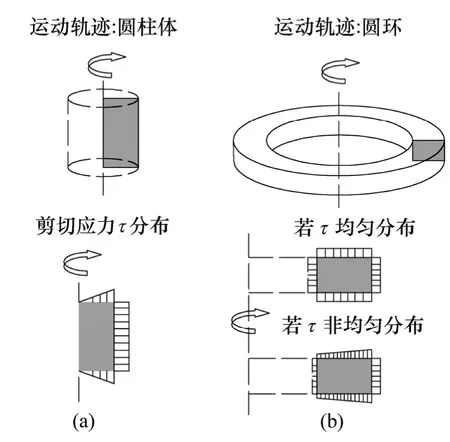
图2 不同构件运动轨迹及应力分布模型Fig.2 Trajectory and stress distribution model of different component

支架克服浆体的屈服应力才能够转动，转动使周围一定区域内的浆体发生剪切作用。桨叶的最大扭矩(Tz)可以认为是由剪切圆柱体侧面扭矩(Ts)和上下端面的扭矩(Te)叠加作用产生，即

将扭矩表示为剪切应力的函数，则上式变成：

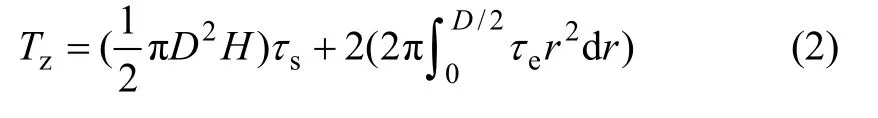
式中：D为剪切圆柱体直径，m；H为剪切圆柱体高度，m；R为剪切圆柱体半径，m；τe为剪切圆柱体上、下端面剪切应力，Pa；τs为剪切圆柱体侧面剪切应力，Pa。

由于深锥内部流动区料浆在同一高度上的浓度基本相同，且支架上下浓度变化较小，因此可以假设τe=τs，且均匀分布在圆柱体上[8]。由于尾矿浆或矿浆属于剪切稀薄流体，随剪切的进行，表观黏度降低[9]，剪切应力的最大值位于浆体屈服流动的时候，即取屈服应力 τy代替 τe和 τs。

鉴于上述分析，式(2)简化为：

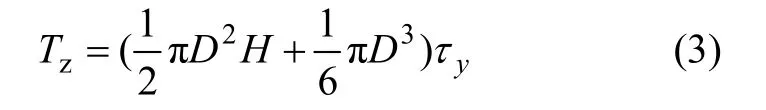
式中：τy为浆体的屈服应力，Pa。

1.3.2 立柱受力分析

立柱浸没在浆体中，克服浆体的屈服应力而转动，转动扫过的面为一圆环体，产生4个剪切面，内外圆柱面和上下圆环面。其受力分析见图 2，当立柱半径较小时，可以认为应力均匀分布。由于立柱一般是固定在支架与刮泥耙上，其转动过程中扫过的上下圆柱面已包含在支架和刮泥耙的受力分析中，不再考虑。

由上述受力分析知，立柱运动时的最大扭矩为：

式中：Tl为立柱所受最大扭矩，N·m；r2和 r1分别为外圆柱面和内圆柱面的半径，m；h为立柱高度，m。

对于多立柱的浓密机，只需要将各立柱所受的扭矩叠加即可：

式中：k为立柱总数。

1.3.3 刮泥耙受力分析

由于散体区尾砂覆盖了刮泥耙，因此刮泥耙的运动对尾砂产生剪切作用，需要克服堆积尾砂的抗剪强度。散体的抗剪强度是指堆积的固体颗粒抵抗剪切破坏的能力。抗剪强度可以用 Mohr-Coulomb理论解释[10]，其公式表达为：

式中：τf为散体的抗剪强度，kPa；c为内聚力，kPa；σ为作用在剪切面上的法向应力，kPa；φ为内摩擦角，(°)。

耙子在运动过程中受力分析如图3所示。图中，w为耙轴转向，r/min；τf为附面层的破坏时的剪切应力，该力是面应力，kPa；a和b分别为刮泥耙实际长度和宽度，m。

图3 刮泥耙受力模型Fig.3 Scraper rake force model

以耙子转动中心为原点建立坐标系(如图3所示)，在耙子长度方向上取微元dx，分析其受力情况，计算刮泥耙转动阻力矩Tg为：

对上式在耙子半径方向上进行定积分，得耙子运动扭矩为：

耙子搅拌过程中，在剪切面上并没有受到法向应力作用，因此，此时的堆积颗粒抗剪强度的值与内聚力的值相等。即τf=c，则上式演化为：

1.3.4 复杂结构搅拌刮泥耙扭矩计算模型

根据上述分析，复杂结构搅拌刮泥耙运动过程中的扭矩(T)由3部分叠加而成，其表达式如下。

对于单立柱的情况，扭矩模型为：

对于多立柱的情况，扭矩模型变为：

2 浆体屈服应力和散体抗剪强度的实验检测

2.1 全尾砂浆屈服应力的检测

2.1.1 检测原理及方法

采用Brookfield R/S型旋转黏度计进行检测，检测原理如图4所示[11-12]。

图4 浆式转子检测方法图Fig.4 Vane detection method

本试验选用转子尺寸为H=4 cm，D=2 cm。Nguyen等[13]认为容器的尺寸及插入的深度应遵循以下比例：Dt/D＞2.0，Z1/D＞1.0，Z2/D＞0.5(图4所示)。本试验容器选用普通500 mL烧杯，Dt=8.5 cm，Z1=5.5 cm，Z2=2 cm。本次试验制备料浆质量分数分别为 72%，74%，76%，78%，80% 5个样品，检测其屈服应力。

2.1.2 试验结果

料浆浓度与屈服应力的关系如图5所示。由图5可以看出：料浆的屈服应力随浓度的上升，呈指数上升，说明浓度对屈服应力的影响显著。其中80%料浆的屈服应力约为72%的4倍。扭矩的最大值发生在剪切最开始的几秒内，随着剪切作用的进行和样品的性质，扭矩逐步降低，最终逼近于1个较低值。因此，对于浓密机的搅拌作用，扭矩最大值是在搅拌开始的最初几分钟。在质量分数为72%～80%时，云南某矿尾砂浆的屈服应力最大值为369.13 Pa。

2.2 散体抗剪强度的检测

2.2.1 散体抗剪强度的测试方法

利用SDJ-II型三速电动等应变直剪仪进行散体抗剪强度测试。分别配制质量分数为86%，88%，90%，92%和 94%的尾砂样(对应含水率 16.28%，13.64%，11.11%，8.70%，6.38%)，浸润过夜。分别施加垂直压力(50，100，150和200 kPa)进行剪切实验。共进行5组浓度的实验。

2.2.2 散体抗剪强度测试结果

内聚力主要是由散体颗粒水膜之间的分子作用力等因素所组成的。内摩擦角-凝聚力-试样含水率关系如图6所示。

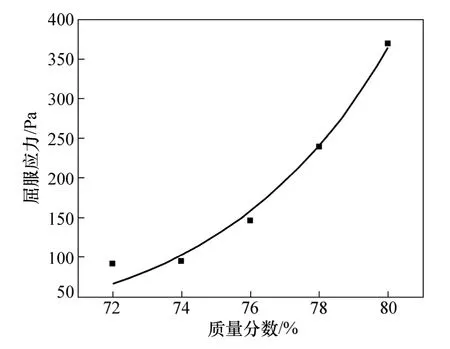
图5 料浆浓度-屈服应力曲线Fig.5 Concentration-yield stress profile

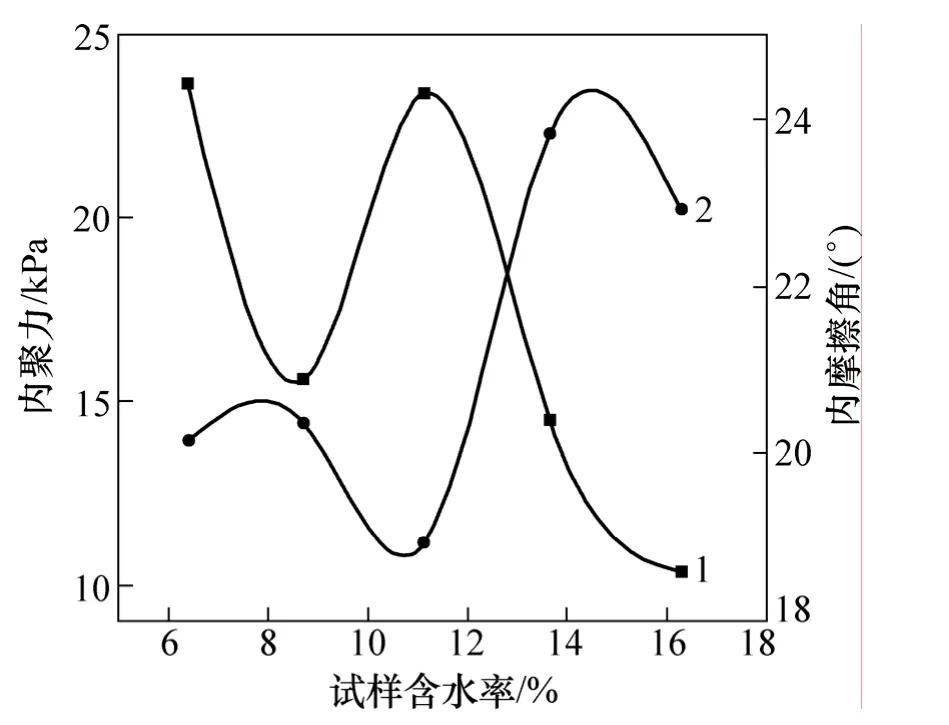
图6 试样含水率和抗剪强度关系曲线Fig.6 Relationship between moisture content and shear strength

从图6可见：随着含水率的减小，内聚力先增大继而下滑、最后上升。一般来说，随着含水率的减少，颗粒间的自由水含量减少，颗粒间的相互滑移也减少，表现出来的内聚力就越大。同时，当水的含量达到一定程度时，颗粒间会形成水膜，在气水界面产生表面张力，故在含水率11%左右时，内聚力达到峰值。随着含水量的继续减少，这层水膜逐渐消失，表面张力作用减少，此时凝聚力又开始下降。最后，随着水分的进一步减少，颗粒间的自由水也越来越少，凝聚力又开始上升。

在深锥中，散体区中附着在锥部机体上的尾砂所能达到的浓度最高，其上限为90%左右，而越靠近刮泥耙的尾砂，其质量分数越低，直到成为流体区。在此，针对云南某矿全尾砂，散体区尾砂所能达到的最高抗剪强度为23.4 kPa。

3 深锥浓密机刮泥耙扭矩验算

3.1 刮泥耙尺寸

某矿使用的深锥浓密机作为尾矿脱水浓缩的主要设备，其耙子尺寸如图7所示。

图7 深锥搅拌耙尺寸图(单位：cm)Fig.7 Dimensions of deep-cone thickener rake

3.2 应力参数确定

根据深锥内部流体区浓度观测值，认为内部平均质量分数为 74%～80%，局部存在 82%左右的高浓度区域，因此，应针对不同浓度选取不同的屈服应力。

对于耙子支架部分，由于高循环位于该处，循环将深锥下部的更高浓度的料浆泵至该处，因此，该部位物料浓度不稳定。根据观测结果，该位置的砂浆最大浓度能够达到78%，对应的屈服应力为τ=239.50 Pa。

由于脱水立柱垂直高度跨度较大，取立柱跨度内砂浆质量分数的平均值作为其计算依据。取质量分数对应76%时的流体的屈服应力，即τ=146.20 Pa。

由于小耙子处于深锥最下部的集料筒中，且小耙子与浓密机底部并未直接接触，下部残留一层散体；因此，该部分的物料以散体计算，最高抗剪强度为τf=c=23.4 kPa。

3.3 搅拌扭矩验算

将深锥耙子尺寸和 2个应力参数代入式(11)，得耙子各构件的扭矩，见表1。

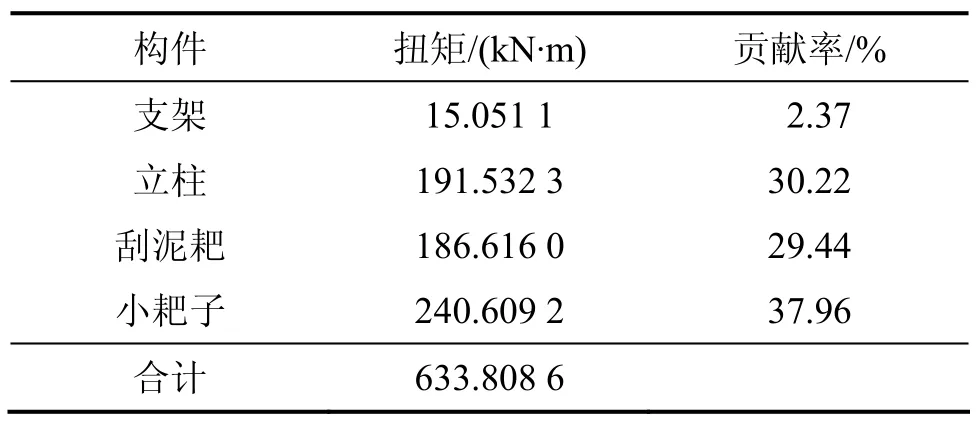
表1 扭矩计算结果Table 1 Torque calculation results

由表1可知：深锥集料筒中的小耙子产生的扭矩最大，达到240.609 2 kN·m，占总扭矩的37.96%。因此，在运行过程中，应着力保持深锥下部集料筒中物料的流动性，当集料筒中部分物料浓度较高或产生分层离析现象后，应采用相应的措施将该部分不合格料浆排出，以降低对深锥扭矩的不利影响。6根立柱所产生的扭矩达到191.532 3 kN·m，占总扭矩的30.22%。因此，为了减小耙子扭矩，在保证强度的基础上，应减小立柱的直径。刮泥耙扭矩达到186.616 0 kN·m，占总扭矩的29.44%，说明在锥部的堆积的尾砂较多，较密实，应注意对该处尾砂的清理，减小对耙子运行的影响。耙子支架部分影响较小，由于支架断面较小，所处位置尾砂浓度较低，因此，扭矩较低。

根据计算结果，当深锥内部各种负面因素同时发生时，产生的扭矩可达633.808 6 kN·m。深锥的设计最大扭矩为650.200 0 kN·m，且为了防止设备过载，当扭矩达到满扭矩的80%时(520.160 0 kN·m)，立即自动停机保护，最大扭矩超出停机保护额定值21.85%。因此，在诸多因素组合在一起共同作用时，搅拌耙扭矩很容易超过该过载保护值。一旦保护停机，无法重新启动，造成压耙事故。因此，该模型可以作为深锥浓密机驱动参数设计的验算方法。

4 结论

(1) 深锥浓密机机体内部存在流动区和散体区两大区域。流动区包含传统意义上的四大区域划分；散体区主要是尾砂在机体上形成的附面层，浓度极高，没有流动性，且对刮泥耙的运行影响较大。

(2) 基于流变学和散体力学分析方法，分别对不同区域耙子的构件进行受力分析，建立了各构件的扭矩计算模型，并最终建立复杂结构搅拌刮泥耙扭矩计算模型。

(3) 针对某矿工程实际，利用建立的扭矩模型对浓密机驱动参数进行验算，扭矩最大值为 633.808 6 kN·m，值超出停机保护额定值 21.85%。小耙子产生的扭矩占耙子总扭矩的37.96%，扭矩贡献最大。这一结果从理论上解释了压耙和压耙后无法启动的现象。因此，该模型可以作为深锥浓密机驱动参数设计的验算依据。

[1]陈述文, 陈启平. HRC高压浓缩机的原理, 结构及应用[J].金属矿山, 2002(12): 33-36.CHEN Shu-wen, CHEN Qi-ping. Principle, structure and application of HRC high pressure thickener[J]. Metal Mine,2002(12): 33-36.

[2]周爱民, 古德生. 基于工业生态学的矿山充填模式[J]. 中南大学学报: 自然科学版, 2004, 35(3): 468-472.ZHOU Ai-min, GU De-sheng. Mine-filling model based on industrial ecology[J]. Journal of Central South University of Technology: Science and Technology, 2004, 35(3): 468-472

[3]王卫, 谭建平. 深锥浓密机刮泥功率的确定及絮凝沉降实验研究[J]. 矿冶工程, 2004, 24(1):44-47.WANG Wei, TAN Jian-ping, Determination of slob-scraper power of deep-cone thickener and experimental study of flocculant settlement[J]. Mining and Metallurgical Engineering,2004, 24(1): 44-47.

[4]姜立春, 吴爱祥, 沈慧明. 散体结构边坡体振动波传播机理[J]. 中南大学学报: 自然科学版, 2003, 34(6): 678-682.JIANG Li-chun,WU Ai-xiang,SHEN Hui-ming. The mechanism about vibrating wave transmitting on the granular structure slope[J]. Journal of Central South University of Technology:Science and Technology, 2003, 34(6): 678-682.

[5]焦华喆, 王洪江, 吴爱祥等, 全尾砂絮凝沉降规律及其机理[J]. 北京科技大学学报, 2010, 32(6): 702-707.JIAO Hua-zhe, WANG Hong-jiang, WU Ai-xiang, et al. Rule and mechanism of flocculation sedimentation of unclassified tailings[J]. Journal of University of Science and Technology Beijing, 2010, 32(6): 702-707.

[6]刘晓辉, 吴爱祥, 王洪江, 等. 膏体充填尾矿浓密规律初探[J].金属矿山, 2009(9): 38-41.LIU Xiao-hui, WU Ai-xiang, WANG Hong-jiang, et al.. A primary Discussion on the thickening law of paste-fing[J]. Metal Mine, 2009(9): 38-41.

[7]WU Ai-xiang. Granular dynamic theory and its applications[M].Metallurgical Industry Press & Springer, 2008: 134-135.

[8]Bassoullet P, Le Hir P. In situ measurements of surficial mud strength: A new vane tester suitable for soft intertidal muds[J].Continental Shelf Research, 2007(27): 1200-1205.

[9]Friend P L, Ciavola P, Cappucci S, et al. Biodependent bed parameters as a proxy tool for sediment stability in mixed habitat intertidal areas[J]. Continental Shelf Research, 2003, 23:1899-1917.

[10]Palchik V. Application of Mohr–Coulomb failure theory to very porous sandy shales[J]. International Journal of Rock Mechanics and Mining Sciences, 2006(10): 1153-1162.

[11]Alderman N J, Meeten G H. Vane rheometry of bentonite gels[J].Non-Newtonian Fluid Mech, 1991(39): 291-299.

[12]Liddel P V, Boger D V. Yield stress measurements with the vane.J. Non-Newtonian[J]. Fluid Mech, 1996, 63: 235-261.

[13]Nguyen N Q, Boger D V. Direct yield stress measurement with the Vane method[J]. Journal of Rheology, 1985, 29(3): 335-347.