基于伪随机序列调制的混合域自适应盲水印算法

韩绍程，王玉松

（中国民航大学基础实验中心，天津 300300）

随着数字多媒体信息在网络中的广泛使用和传播，数字媒体的安全、知识产权的保护和认证等方面问题也变得日益突显，数字水印作为一种有效的解决途径，可以弥补传统加密技术的不足，成为国内外学术界研究的热点[1]。水印算法按照水印嵌入方式的不同，大致分为两类：空域方法和变换域方法。在图像的变换域中嵌入水印，对常见的信号处理操作能具有较好的鲁棒性，使得变换域方法备受关注。图像离散余弦变换（DCT）后，变换系数具有很好的能聚特性且几乎不相关，重构图像时，误差随机分布到各个像素中，不会造成误差积累[2]。小波变换（DWT）因其良好的空频局部化特性，在图像模式识别领域得到广泛应用。小波变换的多分辨率分解和人眼视觉特性是一致的，使其在新一代静止图像压缩标准(JPEG 2000)和运动图像压缩标准（MPEG-4）中占据了重要位置[3]。因此，基于DCT和DWT的方法一直受到人们的重视，出现了一些有效的水印方法[4-6]，但这些算法仍有待完善。多小波作为小波的新发展，许多性能与单小波相比更具有优越性，不少研究者已将水印嵌入到图像的多小波变换域（DMWT）中，达到了较好的实验效果[7-8]。

文献[2]和文献[9]分别是在DCT变换域以及DWT和DCT混合变换域中，采用随机数调制技术实现水印的嵌入，并取得了较好的实验效果，但仍存在一些不足。本文在此基础上进行了改进，以彩色图像作为研究对象，在多小波变换和离散余弦变换混合域内实现了有意义二值水印信息的嵌入和盲提取，水印嵌入前，根据纹理和能量特征，对待嵌入水印的多小波中频系数块进行分类，嵌入水印时，按照分类结果自适应的选择嵌入强度，使算法在不可见性和鲁棒性之间取得了较好的折中。同时，结合Arnold变换和混沌加密技术预处理水印信息，保证了算法的安全性。

1 水印算法设计

1.1 水印图像预处理

为消除水印图像像素空间的相关性，提高数字水印算法的安全性能，在水印嵌入前需对水印图像进行加密预处理，本文结合Arnold变换和Henon二维混沌系统[10]预处理待嵌入的水印图像，具体步骤如下：

1）利用Arnold变换（见式（1））对水印图像W进行K次迭代运算，以实现对W的置乱，其中（x，y）和（x′，y′）为变换前后位置坐标，M为图像大小，由于Arnold变换具有周期性，只须对待恢复的图像进行TK迭代运算，即可得到置乱前的图像，这里T为变换周期。Arnold变换定义如下

2）利用Henon混沌映射（见式（2））产生两个混沌序列 X=｛xi，1≤i≤N × N｝和 Y=｛yi，1≤i≤N × N｝，其中a、b和x0、y0已知，分别从序列中选取M×M个元素，通过判断阈值 Τ，即 xi，yi＞ Τ 时，Zk=1，否则 Zk=0得到两个二值混沌序列ZX=｛zk，1≤k≤M×M｝和ZY=｛zk，1≤k≤M×M｝。随后将ZX和ZY扫描成二维矩阵的形式，记为 X*和 Y*。这里 a、b和初始值 x0、y0可作为密钥使用。Henon混沌映射定义如下

3）将步骤1）中置乱后的结果与X*和Y*进行异或运算，得到加密后的二值信息W*，W*为实际要嵌入的水印信息，即

1.2 多小波系数块分类

为使算法具有一定的自适应性，在鲁棒性和不可见性之间取得更好的折中，水印嵌入前需要对待嵌入区域的多小波中频系数进行模糊分类，在此借鉴了文献[11]中提出的方法。

1）基于人类视觉模型（HVS）的多小波块分类

结合HVS模型，按照式（4）来判断多小波子块的纹理强度

式中：H0为事先设定好的阈值；n（Uk）表示第k个子图块中绝对值大于H0的所有系数的个数。按图1所示隶属度函数，根据 n（Uk）大小可将 Uk分成 TL、TM和TH，Q1、Q21、Q22、Q3要从多次实验中选取合适的值。

2）基于能量模型的多小波块分类

按式（5）计算各小波块的能量

式中：F（u，v）意义同上；m、n为 Uk的行数和列数。将e（Uk）按从小到大的顺序进行编号，编号号码存放于N中，根据Uk的编号在N中的位置按照如图1所示隶属度函数，将Uk分成EL、EM和EH三类。

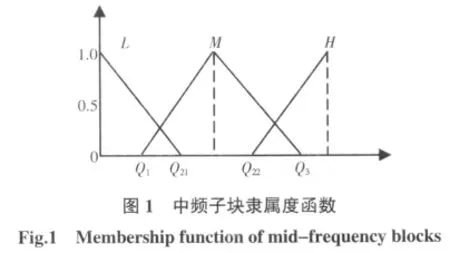
综合考虑以上两种分类情况来确定最终的水印嵌入强度，在强纹理和能量小的多小波子块中适合嵌入较大强度的水印信息。这里结合多小波块的纹理和能量特性，可将待嵌入水印区域分成5类（见式（6））

其中，脚标数值较大的子块，可嵌入较大强度的水印。

1.3 水印嵌入与提取

1）水印嵌入过程

水印嵌入具体步骤如下：

Step1 将原始RGB彩色图像I转换到YIQ空间，并提取Y分量，记为Y，并将其数值扩展到[0，255]区间，即Y=255×Y。

Step2 先对Y分量进行Cardbal2平衡多小波变换，随后对得到中频子带再分别进行一次变换，得到最终的中频子图 LH12、HL12、LH22和 HL22，如图 2（a）所示，并将其按照一定的顺序，组成新的系数矩阵V，如图2（b）所示，作为水印的嵌入区域。

Step3 对系数矩阵V进行8×8分块，并按照1.2介绍的方法对其分类。随后对每一个系数子块Uk应用DCT变换，在变换后的系数中，按照如图2（c）所示的方案，选出若干个中频系数进行调制，约定待调制的系数为Dk。

Step4 通过密钥key1、key2产生2个长度为l的伪随机数p0和p1，l和前面所选的DCT中频系数的个数相同。

Step5 对应每一个Uk嵌入W*的一位水印信息，嵌入规则如下

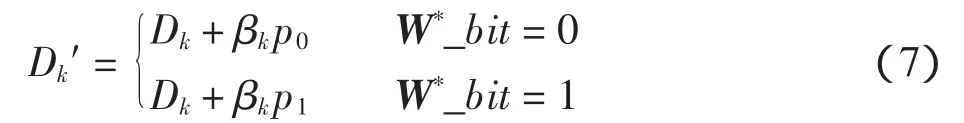
式中：βk为随机序列的调制强度，按照前面分类的结果确定βk的值，即

式中：β_small，β_middle-，β_middle，β_middle+，β_big 的值经过反复实验来获得。

Step6 将修改后的系数还原到Y分量中，并结合I和Q分量恢复到RGB彩色空间，得到含水印的载体图像。

2）水印提取过程

含水印的图像在经历一定的攻击操作后，提取水印时只需计算相应位置的系数D*分别与p0和p1的相关值，通过比较大小来提取水印信息将提取出的二值图像信息经过Arnold反置乱和混沌解密得到最终的水印信息W′

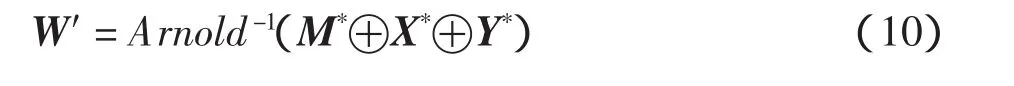
2 实验结果

本文在Matlab7.5环境下进行了大量的仿真实验，选用512×512大小的REG彩色图像作为载体测试图像，它们是 Lena、Baboon 和 House，如图 3（a）～图3（c）所示，采用有意义的二值图像作为水印图像，大小为 32×32，如图 3（d）所示。实验中，Arnold 变换的置乱次数为 24，Henon 序列初值 a=1.4，b=0.3，x0=y0=0，嵌入强度分别取 β_small=15，β_middle－=20，β_middle=25，β_middle+=30，β_big=35。

实验中采用峰值信噪比（PSNR）和归一化相似度（NC）[12]来评价提出算法的性能。PSNR值大于35时，视觉上很难分辨出图像发生的变化；NC值越高，越能说明提出的水印与原始水印之间的相似性。以Lena图为例，按照本文提出的算法，PSNR=35.337 6；在没有任何攻击的情况下，提取出的水印NC=1.000 0，说明该算法的隐蔽性达到了理想的效果。

分别对含水印的图像进行添加高斯噪声、添加椒盐噪声、JPEG压缩和几何剪切等常见的攻击操作，以检验本算法的鲁棒性。由表1可以看出，含水印图像经历不同强度的噪声攻击、不同程度的JPEG压缩和较大范围的几何剪切之后，图像质量严重受损，但提取出的水印基本清晰可见，与原始水印相比具有较高的相似度。

为进一步验证算法的鲁棒性，将本文算法和文献[2]、文献[9]提出的算法进行了比较。通过选择不同的嵌入强度，在保证含水印图像具有近似相同的视觉质量前提下，分别进行了添加高斯噪声（0.01）、添加椒盐噪声（0.04）、JPEG 压缩（Q=80%）和剪切（左上1/4）四种典型攻击操作，表2给出了以Lena图像为载体测试图像，利用不同算法提取出的水印相似度比较情况，图 4（a）和图 4（b）分别显示了用 Baboon和 House两幅图像为测试图像，采用不同算法提取水印的NC值随不同攻击变化的关系。从表2中NC的大小关系不难看出，本文算法更具优势，特别是抵抗剪切攻击的能力，明显优于文献[2]和文献[9]提出的算法。图4进一步说明本文算法相对与于其他算法的有效性，同时证明了该算法具有一定的普适性。

表2 Lena图算法鲁棒性比较Tab.2 Robustness comparison for Lena

3 结语

本文将多小波变换和离散余弦变换的优点有机结合，提出了一种基于伪随机序列调制的混合域水印算法，将水印嵌入到彩色图像的Y分量上，水印检测不需要原始载体图像，实现了水印的盲提取。水印嵌入前采用模糊分类技术处理待嵌入水印区域，水印嵌入时根据Y分量图像多小波变换后的纹理和能量特征，对不同的多小波系数矩阵选择不同的嵌入强度，使得算法具有一定的自适应性。水印嵌入前，采用Arnold变换和混沌加密技术置乱水印，算法安全可靠。实验证明，本文提出的算法对噪声、JPEG压缩和剪切等常见的攻击操作均具有较强的鲁棒性。除此之外，该算法在增大水印信息嵌入容量和抵抗平移、旋转等几何攻击方面有待进一步研究和完善。

[1]COX I J，MILLER M L，BLOOM J A.Digital Watermarking[M].USA:Morgan Kaufmann Publisher，2002.

[2]ZHU HUAIHONG，TIAN LI，MA JINGWEN，et al.A Dual Pseudo Random Sequence Digital Watermarking Algorithm Based on DCT[C]//ICEE，2011:1-4.

[3] 黄达人，刘九芬，黄继武.小波变换域图像水印嵌入对策和算法[J].软件学报，2002，13（7）：1290-1296.

[4]吕秀丽，卞红雨，于 波.基于SVR和DCT的数字图像水印算法[J].系统工程域电子技术，2011，33（5）：1187-1190.

[5] 陈 军，张 伟，杨华千.一种基于小波变换和神经网络的数字水印算法[J].计算机科学，2011，38（6）：142-144.

[6] 周亚训，金 炜.一种小波和余弦变换组合域内鲁棒的自适应零水印算法[J].光电工程，2011，38（5）：80-85.

[7] 苟意远，陈晓鸥.基于CL多小波的数字水印技术[J].中国图像图形学报，2003，8A（5）：572-577.

[8] 胡社教，谢锦生，江 萍，等.基于平衡多小波与神经网络的图像水印算法[J].系统仿真学报，2008，20（11）：2995-2998.

[9]SAIED AMIRGHOLIPOUR KASMANI，AHMADREZA NAGHSHNILCHI.A New Robust Digital Image Watermarking Technique Based On Joint DWT-DCT Transformation[C]//ICCIT，2008，2:539-544.

[10]郑 凡，田小建，范文华，等.基于Henon映射的数字图像加密[J].北京邮电大学学报，2008，31（1）：66-70.

[11]王琛晖，舒志彪.基于小波包变换和块模糊分类的自适应水印算法[J].计算机工程与应用，2004，40（30）：54-56.

[12]韩绍程，罗长杰，张兆宁.基于多小波变换和分块SVD的彩色图像水印算法[J].工程图学学报，2010（2），128-133.