反复水平荷载下常偏压箱形钢柱抗震性能试验

罗永峰，李海锋，2，李德章，丁大益

（1.同济大学 建筑工程系，上海200092；2.华侨大学 土木工程学院，福建 厦门361021；3.合肥市重点工程建设管理局，安徽 合肥230001；4.五洲工程设计研究院，北京100053）

箱形截面钢构件在两个主轴方向均有较大的抗弯刚度及良好的抗扭刚度，因而受力性能良好，广泛应用于现代大型复杂钢结构中，在高层钢结构建筑和现代大跨度空间钢结构中尤为多见.在实际钢结构工程中，为了减轻用钢量及构件自重，减小地震与温度效应，设计时尽量采用薄壁箱形截面构件.我国现行《建筑抗震设计规范》［1］对梁、柱宽厚比的限值，仅针对多高层框架结构，对大跨度钢结构箱形构件壁板的宽厚比没有明确的限值.大跨度钢结构构件的受力特点与多高层框架结构差异很大，如前者的柱子要承受一定的轴力和很大的弯矩，而后者则以承受轴力为主.实际上，我国现行规范对宽厚比限值的规定，主要参考美、日的国家规范，并未深入研究钢材加工的构件；同时，理论上主要来自于静力作用下箱形截面壁板在简单应力状态和简单变形状态下的研究成果，并没考虑地震作用下的反复应力状态以及板件中可能存在的复杂应力状态及相互间的作用效应.因此，规范针对多高层框架结构规定的宽厚比限值不应直接应用于大跨度钢结构中，应该根据后者的受力特点，并针对国产钢材制作的构件，深入研究大跨度结构中箱形钢构件的抗震性能，进而提出箱形构件壁板宽厚比的合理限定.

基于上述情况，笔者研究箱形钢柱在偏心常轴力、柱顶反复水平荷载作用下的滞回性能，选择轴压比、腹板宽厚比、柱顶弯矩为主要变量，进行了4组共16根箱形钢柱的拟静力试验.以荷载－位移滞回曲线、骨架曲线、延性系数等指标，综合评价箱形钢柱的抗震性能，为确定大跨度钢结构箱形构件壁板宽厚比限值，提供有价值的实验数据和参考资料.

1 试验概况

根据一实际大跨度钢结构工程中柱子的受力特点，选取一箱形压弯柱为研究对象.该柱简化模型的上端作用有偏心常轴力和反复水平荷载，如图1所示.图中，N表示轴力，V表示水平荷载.

图1 试验分析简图Fig.1 Diagram for experimental analysis

1.1 试件设计

试验共设计了2种试件，编号分别为I和II.I试件为长柱，II试件为短柱，每种试件又分A，B两组，每组均包含3个不同腹板宽厚比的试件，其中第1个试件的腹板宽厚比满足现行抗震设计规范要求，其余试件的腹板宽厚比超出现行抗震设计规范的限值.试件设计图如图2所示，试件参数列于表1、表2中.所有试件的材料均为Q345B.

1.2 试验加载系统与加载制度

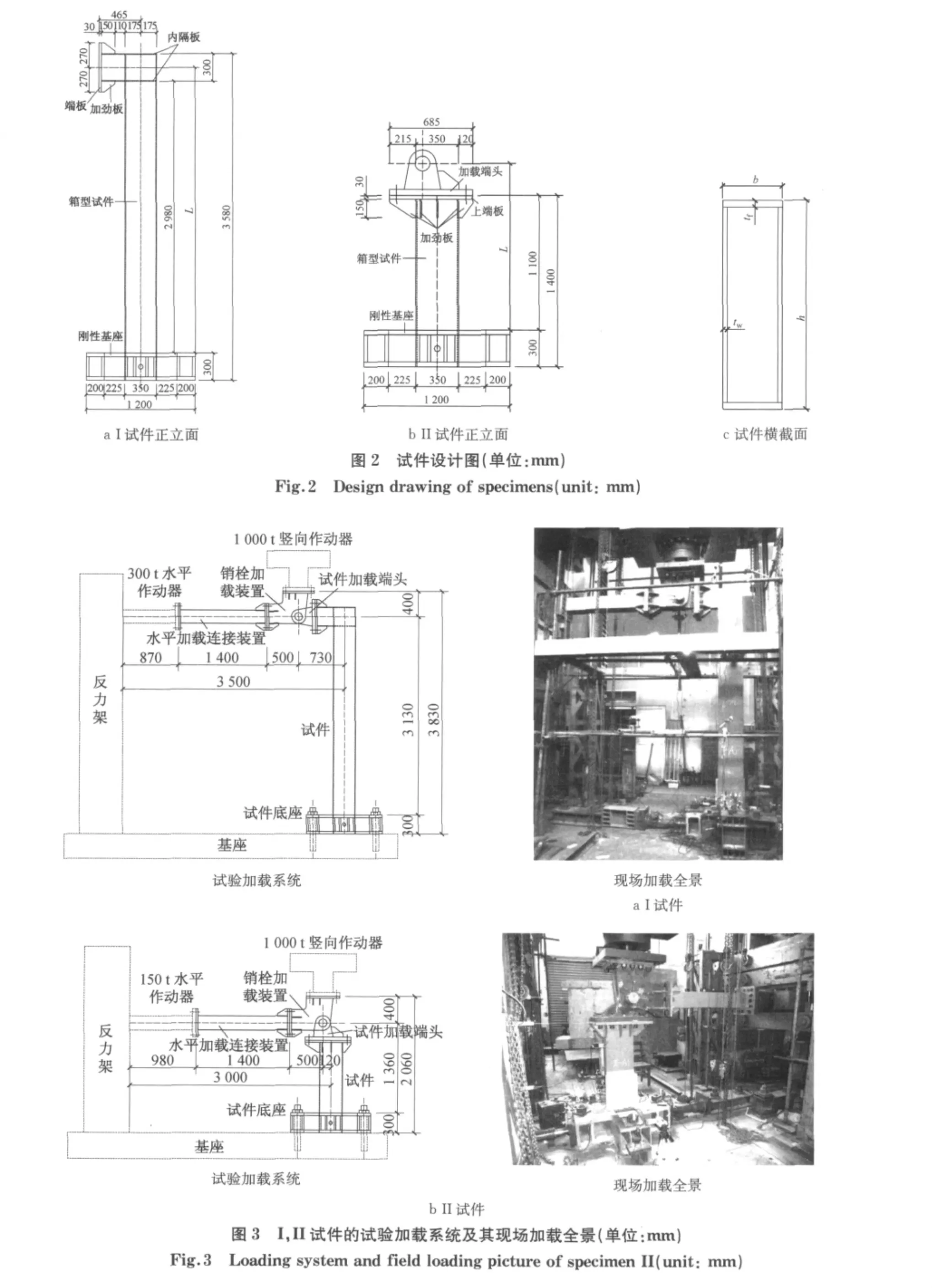
试验采用同济大学1 000t大型多功能静电液伺服系统，I试件和II试件的试验加载系统及现场加载全景如图3所示.为了模拟箱形柱的实际边界条件，采取以下构造措施：①以锚栓及托座固定柱下端，形成固定端.②以柱顶销栓铰接柱顶，同时施加柱顶偏心轴力和柱顶反复水平荷载.

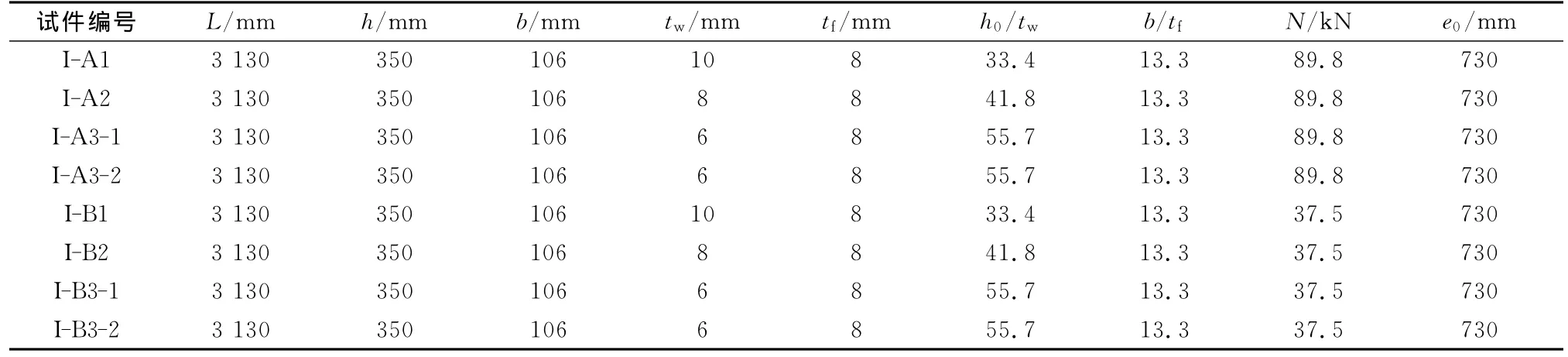
表1 I试件设计参数Tab.1 Design parameters of specimen I

试验加载由水平位移控制，柱顶反复水平位移加载制度为：① 屈服前，按0.5δy，0.75δy加载；② 屈服后，按δy，2δy，3δy，4δy…加载；③ 屈服前每级加载循环2圈，屈服后每级加载循环3圈.δy为试件受力最大纤维出现屈服时的柱顶侧向位移.柱顶反复水平位移加载制度如图4所示，n表示循环次数.

图4 柱顶反复水平位移加载制度Fig.4 The method of cyclic lateral loading

1.3 测点布置

测试的数据有：柱顶加载点水平荷载和位移，腹板表面应力变化及屈曲变形，翼缘板应力变化及屈曲变形.为了考察柱底刚接性态，还需监测托座的转动及平移.柱顶加载点水平荷载由MTS伺服系统的数据采集系统自动生成，腹板屈曲用光栅监测，其余数据需布置应变片和位移计进行测量.翼缘板、腹板上应变片和位移计的布置见图5，刚性基座上位移计布置见图6.

根据光栅［2－4］产生的云纹变化来监测腹板的屈曲现象，不需要推算腹板的变形值.采用自制光栅片监测腹板的局部屈曲现象.试件栅的尺寸为350mm×350mm，布置在试件根部一侧腹板上.布置时应使试件栅与腹板紧密粘结，保证两者共同变形.基准栅固定在自制方形铁框上，方形铁框与试件栅间的距离可调.加载时，用摄像机记录光栅云纹变化.自制光栅监测系统如图7所示.

2 试验现象

有4个试件测得的数据与理论分析结果存在较大差异，试验结束后切开腹板查看后发现，实际试件壁厚与设计不符，试件I－A1实际腹板厚度为6mm而非10mm；试件I－B3－1实际腹板厚度为10mm而非6mm；试件II－A3－2实际腹板厚度为8mm而非6 mm，试件II－B2实际腹板厚度为6mm而非8mm.

为对比分析试件在柱顶反复水平荷载作用下的抗震性能，可将试验现象分组比较，I－A，I－B，II－A，IIB组试件的试验现象分别见表3，4，5，6.翼缘板和腹板的编号如图6所示.

对比分析表3～6中试验现象可知：

图6 刚性基座位移计布置Fig.6 Displacement meter arrangement in support

（1）腹板宽厚比是影响腹板屈曲荷载的主因，腹板屈曲荷载、破坏荷载随腹板宽厚比增大而减小.

图7 光栅监测系统Fig.7 Monitoring system by grating

（2）柱顶竖向力在腹板平面外的偏心对腹板最终变形形态影响很大.若轴力在腹板平面外的偏心小于b／8（b为翼缘板宽度），试件壁板屈曲变形为一个半波，腹板外凸，翼缘板内凹，变形基本对称.若轴力在腹板平面外的偏心大于b／8，腹板内凹屈曲.

（3）塑性变形主要集中在柱根部（固定端）区域，一般始于距固定端0.1h（h为腹板宽度）处，最大塑性变形出现在距固定端0.4～0.5h处，塑性变形终止于距固定端0.7～0.8h处.

（4）破坏模式可分为4类：a类，破坏以塑性变形为主；b类，距柱根部一定高度（约50～100mm），翼缘板断裂；c类，翼缘板在柱根部焊接热影响区断裂；d类，柱根部区域翼缘板与腹板连接焊缝撕裂.试件II－B1，II－B3－1，II－B2的破坏模式属a类；I－A2，I－A3－1，II－A3－2，II－A3－1 属 b；I－A1－2，II－A1，II－A2属c；其余试件破坏模式属d.图8为破坏模式照片.

图8 试件破坏模式Fig.8 Failure modes of specimens

3 抗震性能分析

3.1 荷载－位移滞回曲线

本节仅给出I－A组试件的荷载－柱顶位移滞回曲线［5－6］，如图9所示.图中，纵坐标为作用于试件销铰中心的水平荷载V，横坐标为对应的水平位移δ，取柱顶位移计D19（见图10）的测量值，消除基座刚体转动及平移的影响.基座刚体位移如图10所示.可采用下式消除基座刚体转动及平移的影响：

式中，D为位移计D2与D5之间的水平距离.

分析图9可得：

（1）腹板宽厚比是影响试件滞回曲线的最主要因素.腹板宽厚比越大，滞回曲线越不饱满，加载后期构件承载力、刚度的退化越严重.

（2）当柱顶水平位移大于δy后，随着反复水平位移的增大，试件刚度逐渐降低；但卸载刚度基本不变，与初始弹性刚度大体相同.

（3）加载后期，在同级柱顶水平位移反复循环加载三次后，每次循环加载所得的最大承载力均有所下降，表明试件强度退化.

（4）所有试件的滞回曲线基本为饱满梭形，没有明显的捏拢现象，表明试件有良好的抗震性能.

图10 基座刚性位移示意图Fig.10 Displacement of rigid support

3.2 骨架曲线

试验的主要参数为腹板宽厚比、柱顶轴力、柱顶弯矩.为分析各变化参数对试件抗震性能的影响，现引入以下参数：

表3 I－A组试件的试验现象Tab.3 Experimental phenomena of specimen I－A

表4 I－B组试件的试验现象Tab.4 Experimental phenomena of specimen I－B

式中：Mp为塑性弯矩；Np为塑性轴力；φ为试件转角；n为轴压比；m为柱顶弯矩比值；M为柱底弯矩.

表5 II－A组试件的试验现象Tab.5 Experimental phenomena of specimen II－A

表6 II－B组试件的试验现象Tab.6 Experimental phenomena of specimen II－B

3.2.1 腹板宽厚比对骨架曲线的影响

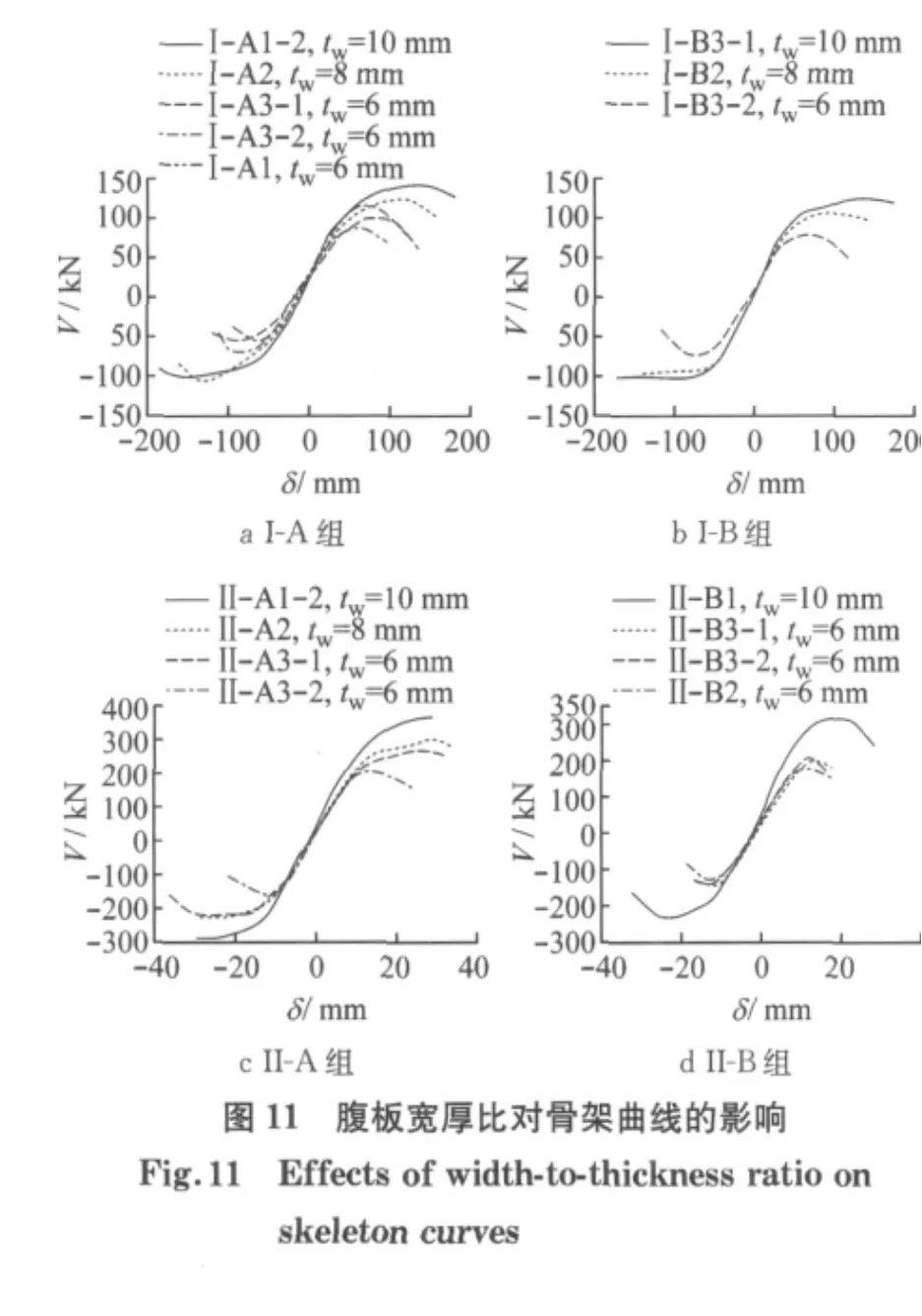
为了考察腹板宽厚比对骨架曲线［7］的影响，图11分别给出了I－A，I－B，II－A，II－B组试件的骨架曲线，各组的柱顶轴力、柱顶弯矩相同.

分析图11可得：

（1）腹板宽厚比相同的试件，骨架曲线基本相同，腹板宽厚比越大，骨架曲线包围的面积越小.

（2）在柱顶反复水平位移加载过程中，因柱顶弯矩作用，与柱顶弯矩效应一致的柱顶拉力（V为负值）比柱顶推力（V为正值）小，导致骨架曲线不对称.

（3）试件刚度、承载能力及滞回曲线包围的面积，随腹板宽厚比增大而减小，极限承载力对应的位移也减小.腹板宽厚比越大，骨架曲线下降越陡，表明加载后期承载力退化及刚度退化现象越严重.

3.2.2 柱顶荷载对骨架曲线的影响

为了考察柱顶荷载对骨架曲线的影响，图12分别给出了腹板厚度tw＝10mm，8mm，6mm试件的量纲一的骨架曲线.

分析图12可得：

（1）I试件的极限转角，腹板厚10mm（h0／tw＝33.4）的为约为6%，8mm（h0／tw＝41.8）的约为5%，6mm（h0／tw＝55.7）的约为3%～4%.II试件中，腹板厚10mm（h0／tw＝33.4）和8mm（h0／tw＝41.8）的极限转角约为2%，6mm（h0／tw＝55.7）试件约为1.5%.表明腹板宽厚比及柱顶荷载越大，试件的变形能力越差.

（2）柱顶弯矩对构件抗震性能的影响相对较小.轴压比对构件抗震性能的影响较大，当轴压比n≤0.1时，轴力对构件抗震性能的影响较小，可以忽略；当n＞0.1时，影响明显变大，不能忽略.

（3）只有腹板宽厚比和轴压比都最大的试件IIB2，II－B3－1，II－B3－2没有达到截面的塑性弯矩，但已非常接近，其余试件均达到.

3.3 位移延性系数

以位移延性［8－9］系数μ研究构件的延性特征

式中，δu为构件的极限位移.计算μ时，必须根据试验所得的荷载－位移骨架曲线确定其δu／δy.由于实际试件的受力变化过程并非理想弹塑性，其荷载－位移曲线没有明显的屈服点，所以屈服位移的确定存在一定的困难.本试验的δy取构件受力最大纤维屈服时柱顶侧向加载点位移，极限位移δu取试件破坏荷载点对应的柱顶侧向加载点位移，破坏荷载点由第2节中规定的破坏模式判定.各试件在屈服状态、最大荷载点、破坏荷载点对应的柱顶水平荷载Vy、水平位移δy、相对变形x及延性系数μ如表7所示.

由表7可知，大部分试件的μ均大于3.0，约为3.0～6.5，抗震性能良好.由于柱顶弯矩的影响，与柱顶弯矩效应相反的柱顶正向延性（V为正值）好于反向延性（V为负值）.由于破坏模式不同，不同试件在破坏荷载点对应的柱顶水平力Vu与最大荷载点对应的柱顶水平力Vmax的比值Vu／Vmax相差较大.tw＝10mm（h0／tw＝33.4）试件的Vu／Vmax＞90%，tw＝8mm（h0／tw＝41.8）试件的Vu／Vmax＞80%，tw＝6 mm（h0／tw＝55.7）试件的Vu／Vmax≈70%.

4 抗震设计建议

《建筑抗震设计规范》［1］中把构件划分为4个抗震等级.本文综合分析各试件的骨架曲线、位移延性、刚度退化、强度退化、耗能能力，并参考国外相关研究［10－11］，提出如下适用于各抗震等级的定量判定标准：一级，μ≥6，且能达到截面的塑性弯矩；二级，4.5≤μ＜6，且能达到截面的塑性弯矩；三级，3≤μ＜4.5，且能达到截面的塑性弯矩；四级，2≤μ＜3.

根据上述判定标准，并结合试验现象及试件的抗震性能分析，综合判定各试件可适用的抗震等级，见表8.

表7 箱形钢柱试件的位移延性系数Tab.7 Displacement ductility factor of specimens

根据试验结果，可提出大跨度钢结构中箱形钢柱腹板宽厚比h0／tw的限值：一级，50～40n；二级，60～40n；三级，75～50n；四级，85～50n.

对于距柱根部h以上的腹板，宽厚比限值可降低一个抗震等级；对于抗震等级为四级的箱形钢柱，距柱根部h以上的腹板宽厚比限值不再降低要求.

5 结论

（1）腹板宽厚比是影响腹板屈曲荷载的主要因素，试件腹板的屈曲荷载、破坏荷载，随腹板宽厚比增大而减小.

表8 各试件可适用的抗震等级Fig.8 Applicative seismic grades of specimens

（2）柱顶轴力在腹板平面外的偏心，对腹板屈曲变形形态影响很大.若偏心小于b／8，壁板屈曲变形为一个半波，腹板外凸，翼缘板内凹，变形基本对称；若大于b／8，腹板内凹，屈曲变形.

（3）试件塑性变形主要集中在柱根部（固定端）区域，一般始于距固定端0.1h处，最大塑性变形出现在0.4～0.5h处，终止于0.7～0.8h处.

（4）试件的破坏模式可分为4类：① 以塑性变形为主；② 距柱根部一定高度处（约50～100mm）翼缘板断裂；③ 翼缘板在柱根部焊接热影响区断裂；④柱根部区域翼缘板与腹板连接焊缝撕裂.

（5）腹板宽厚比是影响构件滞回性能的最主要因素，宽厚比越大，滞回曲线越不饱满，滞回曲线包围的面积越小；同时骨架曲线下降越陡，表明加载后期试件承载力及刚度退化越严重.

（6）当轴压比n≤0.1时，轴力对构件抗震性能的影响较小，可忽略；当n＞0.1时，影响明显变大，不能忽略.

（7）柱顶弯矩使与其效应相反的正向延性增大，从而降低与其效应相同的反向延性.当构件的柱顶弯矩相差不大时，构件的延性随轴压比的增大而减小.总体来看，轴压比对构件抗震性能的影响较大，柱顶弯矩对构件抗震性能的影响相对较小.

［1］黄世敏，王亚勇.GB50011—2010 建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.HUANG Shimin，WANG Yayong.GB50011—2010 Code for seismic design buildings［S］.Beijing：China Architecture ＆Building Press，2010.

［2］曹起骧.密栅云纹法原理及应用［M］.北京：清华大学出版社，1983.CAO Qixiang.Theory and application of moirémethod［M］.Beijing：Tsinghua University Press，1983.

［3］黄健华，潘庆春.矩形梁极限承载时塑性铰的云纹法试验研究［J］.合肥工业大学学报：自然科学版，2002，25（4）：559.HUANG Jianhua， PAN Qingchun.Moiré experimental investigation of the plastic hinge while the rectangular beams enduring the ultimate load［J］.Journal of Hefei University of Technology，2002，25（4）：559.

［4］曹康，周贤宾.面外云纹法与相位法关系的研究［J］.航空材料学报，1995，15（3）：50.CAO Kang，ZHOU Xianbin.Research on the relations between out－of－plane moirémethod and phase method［J］.Journal of Aeronautical Materials，1995，15（3）：50.

［5］林震宇.L形钢管混凝土构件力学性能若干关键问题研究［D］.上海：同济大学土木工程学院，2008.LIN Zhenyu.Study on some key problems on behavior of L－shaped concrete－filled steel tubular columns［D］.Shanghai：Tongji University.College of Civil Engineering，2008.

［6］李忠献.工程结构试验理论与技术［M］.天津：天津大学出版社，2004.LI Zhongxian.Theory and Technique of Engineering Structure Experiments［M］.Tianjin：Tianjin University Press，2004.

［7］王文达.钢管混凝土柱－钢梁平面框架的力学性能研究［D］.福州：福州大学土木工程学院，2006.WANG Wenda.Behavior of Steel Beam to Concrete－filled Steel Tubular Columns Frames［D］.Fuzhou：Fuzhou University.College of Civil Engineering，2006.

［8］罗金辉.L形钢管混凝土柱－H型钢梁框架节点抗震性能研究［D］.上海：同济大学土木工程学院，2011.LUO Jinhui.Study on Seismic Behavior of Connections between Concrete－filled L－shaped Steel Tubular Columns and H－shaped Steel Beams［D］.Shanghai：Tongji University.College of Civil Engineering，2011.

［9］崔大光.型钢混凝土梁柱框支剪力墙抗震性能研究［D］.上海：同济大学土木工程学院，2006.CUI Daguang.Cyclic Performance of Shear Wall Supported on Frame with Steel Reinforcing ［D］.Shanghai： Tongji University.College of Civil Engineering，2006.

［10］Mazzolani F M，Piluso V.Member behavioural classes of steel beams and beam－columns［C］／／Proceeding of First State of the Art Workshop，COSTI.Strassbourg：［s.n.］，1992：517－529.

［11］Mazzolani F M，Piluso V.ECCS Manual on Design of Steel Structures in Seismic Zones［S］.Brussels：ECCS，1995.