双轮铣槽机传动系统的优化设计
2012-07-28杨诗鸿张志强
杨诗鸿 张志强
(水利部水利建设管理总站 北京 100038) (武汉大学 430072)
张忠生
(水利部水利建设管理总站 北京 100038)
双轮铣槽机是用于大型地下连续墙、防渗墙工程的专用施工设备,它在地下连续墙、防渗墙工程的施工中有着无可比拟的优势,因此实现此类设备的国产化具有重要意义。由多级齿轮传动构成的铣轮传动系统是双轮铣槽机的核心部件之一,具有承载能力要求高、输出转矩大、布置空间小的特点,在满足铣轮输出转矩要求的前提下,通过对铣轮传动系统进行优化设计,减小齿轮传动部件体积,为铣轮内部其他传动部件以及减振器的安装布置留出了充足的空间。
目前齿轮传动系统优化设计研究主要分为两方面:ⓐ齿轮传动系统的传动比分配;ⓑ各传动级的齿轮模数和齿数等参数的优选[1]。而对具有空间尺寸约束的齿轮传动系统优化设计的研究较少。本文对双轮铣槽机传动系统的优化设计进行了深入研究,以最小体积为优化目标,以第一、第二级行星传动的传动比和锥齿轮传动的齿宽系统为设计变量,建立双轮铣槽机铣轮传动系统的优化模型,利用Matlab的优化工具进行优化,求解得到传动环节体积的优化最小值以及相应的各级主要参数,获得了较好的优化效果,明显降低了传动系统的体积,对于传动系统设计具有很好的指导意义。
1 双轮铣槽机传动系统
双轮铣槽机是一个大型的工程机械,包括铣轮传动系统、纠偏系统、排渣系统及卷扬系统等四个部分,各个系统之间相互协调共同完成铣槽的功能。双轮铣槽机行星传动系统方法如下图所示。本方案第一级采用锥齿轮传动,第二、第三级采用NGW型行星传动,传递的扭矩大,效率高[2]。

行星传动系统图
2 行星传动系统优化设计
本文针对目前齿轮传动系统优化设计研究中所存在的各级优化目标单一的缺点,将双轮铣槽机铣轮传动系统的优化设计分为两个部分:整体优化设计和单级优化设计。
整体优化设计以第二、第三级行星传动的传动比和第一级锥齿轮传动的齿宽系数为设计变量,以各齿轮传动的总体积最小为目标函数。三个设计变量都是连续变量,可以规避混合离散变量问题。单级优化设计将以整体优化设计的结果为输入,以小锥齿轮和太阳轮的齿数和模数为设计变量,以与整体优化设计结果相差最小为目标函数。单级优化设计以枚举法进行计算。
2.1 整体优化设计
2.1.1 设计变量和目标函数
整体优化设计以第二级行星传动的传动比i2、第三级行星传动的传动比i3和第一级锥齿轮传动的齿宽系数φR这三个独立参数为设计变量。

整体优化设计以三级传动的总体积最小为目标函数,目标函数为

2.1.2 约束条件
a.边界约束条件。边界约束条件包括传动比,锥齿轮齿宽系数和锥齿轮的传动比等均有一定的取值范围。
b.等式约束条件。两行星级传动比分配的原则是径向尺寸大致相等。而行星齿轮内齿轮分度圆直径基本上决定了行星齿轮的径向尺寸,因此本文按各级内齿轮分度圆直径大致相等分配两行星级传动比。第三级与第二级行星齿轮内齿轮之比为1~1.2,初取1.1。等式约束即为

c.不等式约束条件。径向尺寸约束条件为

轴向尺寸约束条件为

2.2 单级优化设计
由整体优化设计可分别得到设计变量i2、i3、φR的值,由于小锥齿轮分度圆直径de1和第二、第三行星传动太阳轮分度圆直径da2与da3是关于设计变量的函数,故也可由此求出。单级优化设计根据第一步整体优化设计得出的数据来进行。
2.2.1 锥齿轮的优化设计
根据整体优化设计得出大端分度圆直径de1和齿宽系数φR,并由公式得出传动比i1的值,锥齿轮以此为已知条件,进行优化设计。
a.设计变量。锥齿轮单级优化设计以大端模数me和小锥齿轮齿数z1这两个独立参数为设计变量。

b.目标函数为
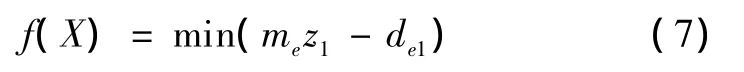
c.约束条件。包括齿数z1为正整数,且12≤z1≤30,me需符合国家标准和强度条件。
2.2.2 行星齿轮的优化设计
行星齿轮的单级优化设计,以整体优化设计得出的传动比ik(k=2,3)及太阳轮分度圆直径dak(k=2,3)为输入进行。
a.设计变量。行星齿轮单级优化设计以太阳轮模数m和太阳轮齿数za这两个独立参数为设计变量。

b.目标函数为
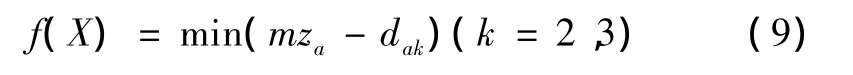
c.约束条件。包括za为正整数,且13≤z1≤30,m需符合国家标准,行星齿轮配齿条件[3]重合度约束,强度条件,不产生过渡曲线干涉约束和齿顶不过薄约束。
3 优化设计结果分析
本文利用Matlab优化工具进行双轮铣槽机传动系统优化设计,对于整体优化设计,采用了Matlab优化工具箱中有约束非线性最小化函数fmincon()函数,同时采用遗传算法工具箱优化对优化结果进行对比。对于单级优化设计,由于设计变量比较少,且设计变量的变化范围不大,以自己编制的程序用枚举法优化。fmincon()函数与遗传算法工具箱优化结果见下表。

两种算法计算结果表
由上表可知,fmincon()函数与遗传算法工具箱优化的结果基本相同,由于遗传算法是基于全局的[4],可见上面的优化结果是全局最优解。同时,对于fmincon()函数的优化,尝试了多组不同的初始值进行,得出的结果基本一致。综上可知求得结果即为全局最优解。原方案的体积为8.6073×106mm3,优化后的体积为8.2896×106mm3,体积减少3.69%,优化效果较好。
4 结语
a.本文给出的双轮铣槽机行星传动系统优化设计方法和利用Matlab优化工具得到的设计参数,能明显地降低传动系统的体积,使结构更加紧凑,减少制造安装成本,并且很好地满足了工作要求。
b.本文对行星齿轮传动系统优化设计进行了深入研究,针对目前齿轮传动系统优化设计研究中所存在的各级优化目标单一的缺点,提出将双轮铣槽机铣轮传动系统的优化设计分为整体优化设计和单级优化设计。优化结果良好,说明该方法合理有效,对类似行星传统系统优化设计提供了有益的参考。◆
1 冯继承.双轮铣槽机铣轮传动系统设计研究[D].武汉:武汉大学,2010:5-7.
2 唐增宝,车荷香.行星齿轮减速器的优化设计[J].煤矿机械,1988(4):57-61.
3 机械设计手册编委会.机械设计手册:第3卷[M].新版.北京:机械工业出版社,2004.
4 王文明.应用遗传算法的齿轮传动优化设计[J].科技资讯,2009(9):7.
