小半径曲线动力学超限成因分析及影响因素研究

孙善超，王卫东，刘金朝

(中国铁道科学研究院 基础设施检测研究所，北京 100081)

曲线线路是轨道结构的薄弱环节，曲线通过是车辆动力学课题中的一个重要方面［1］。车辆在曲线上运行时，各运动部件之间以及轮对与钢轨之间将会产生相对位移，即使是较小的轨道不平顺，也会导致动力学响应的超限。对线路来说，动力学响应的超限将导致轨距扩宽、轨排横移或钢轨翻转，使线路的维修工作量大大增加，甚至危及行车安全。更为严重的动力学超限会使线路的不平顺加剧，从而影响车辆的稳定性。车轮上较大的横向力与较小的垂向荷载联合作用时，车辆的抗脱轨安全性下降。因此，为保证曲线上车辆的通过性能，应合理控制小半径曲线上的轨道几何不平顺超限［1-5］。

1 曲线通过时轮对蠕滑力分析

轮对作纯滚动时，轮对中心所走过的轨迹在轨道平面内的铅垂投影一般称作纯滚线，纯滚线是一段圆弧，它与圆曲线相平行，其曲率中心与圆曲线的曲率中心是重合的。纯滚线总是位于圆曲线线路中心线的外侧。

研究轮对的几何曲线通过时，取纯滚线与径向线作为坐标系统。相应地，轮对相对于该坐标系统的位移中，横摆位移为y*，摇头位移为φ。

假定轮对在曲线上的横向位移不大，轮轨间的接触角较小，可以认为轮轨接触几何关系是线性的，蠕滑规律也是线性的。在不考虑自旋蠕滑时，则沿纵向和横向蠕滑力分量分别为

若蠕滑率采用UIC C116委员会建议的方法，则式(1)可以改写成

式中 Tx，Ty——纵向和横向的蠕滑力分量;

f11，f22——纵向和横向的蠕滑系数;

vx，vy——纵向和横向蠕滑率;

Vrx，Vry——钢轨接触斑上沿 x，y 轴两个方向的速度分量;

Vwx，Vwy——车轮接触斑上沿 x，y 轴两个方向的速度分量;

V——轮对前进速度。轮对在稳态工况下通过右曲线时，内(右)外(左)侧钢轨和车轮接触斑上的各速度分量分别为

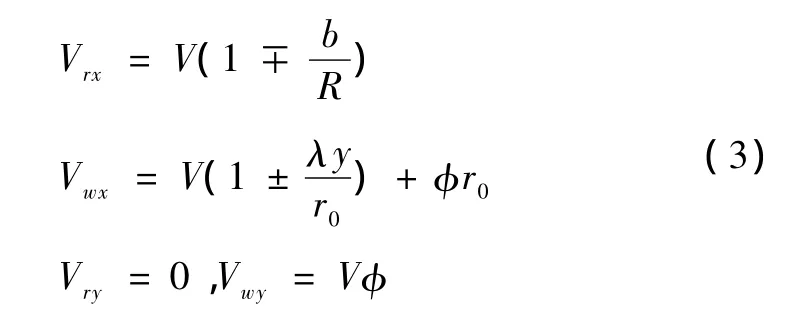
式中 b——轮对左右两车轮滚动圆间的横向距离之半;

R——曲线半径;

λ——踏面斜率;

y——轮对质心距线路中心线的坐标;

r0——车轮标称半径;

φ——轮对实际转速和 V/r0的差值(即轮对绕自身轴的平均转速应为 V/r0+φ)，它与左右轮重的减载量有关。

假定由于超高不足引起的轮重变化率 q=Δp/p(Δp，p分别为轮重变化量和静轮重)。因为蠕滑系数大致与成比例，于是左右轮的蠕滑系数便各不相同。由此计算得出的蠕滑系数 f11和f22须各乘以(1±进行修正。式中对减重的右侧车轮取负号。

在轮对转速为常数的条件下，由纵向蠕滑力引起的合成力偶必等于零，即

式中 Txr，Txl——外轮和内轮的纵向蠕滑力;

rr，rl——外轮和内轮滚动圆半径。

将式(4)代入式(1)，并利用式(2)，式(3)，注意到y=y0+y*(y0为轮对中心相对于线路中心的外移量)，可导出关系式

由此可见，轮对转速的差值 φ和轮重变化率成正比。

左右车轮的蠕滑率分别可写成

相应地，纵向和横向蠕滑力为

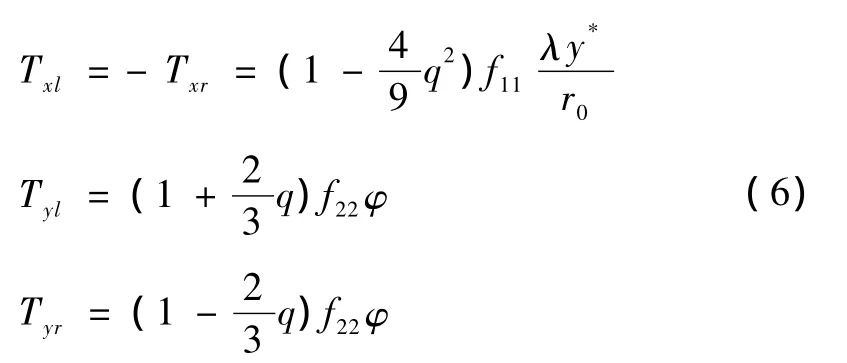
式中 vxl，vyl——内轮纵向和横向蠕滑率;

vxr，vyr——外轮纵向和横向蠕滑率;

Txl，Tyl——内轮纵向和横向蠕滑力;

Txr，Tyr——外轮纵向和横向蠕滑力。

由式(5)可以看出，由于轮重的差异，造成减载的右侧车轮的纵向蠕滑率增大，而增载的左侧车轮的纵向蠕滑率减小，因此，两车轮上的纵向蠕滑力也各不相等，迫使轮对产生一个微小的角位移，直至调整到两车轮的纵向蠕滑力大小相等、方向相反为止，这时的蠕滑力一般略小于轮重相等时的情况。至于左右车轮的横向蠕滑率虽然相等，但蠕滑系数不等，因此两侧车轮的横向蠕滑力也各不相等。

作用在轮对上的合成横向蠕滑力Ty和蠕滑力矩Mz为

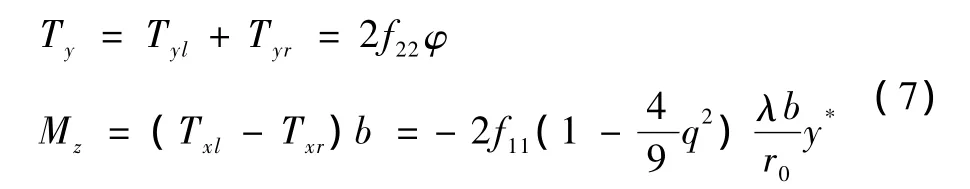
由式(7)可知，横向蠕滑力是由于轮对的摇头角位移产生的，而蠕滑力矩则由轮对位移引起。因此，对于轮对踏面，可以依靠蠕滑力和力矩来导向，完成曲线通过［1，6－7］。而在曲线通过的同时，由于轮对的横移和摇头，缩小了轮轨间的游间，增加了接触轮缘的几率，从而对轨道的几何不平顺更为敏感。以下通过实例对曲线上动力学超限成因进行分析，并对动力学超限的影响因素进行深入分析。

2 动力学模型的建立及试验验证

动力学模型的建立是进行动力学动态特性研究的基础，根据不同研究目的，可以采用不同的建模方法［8］。本文基于虚拟样机技术对车辆的各个部件进行建模，建立的模型可以用来对车辆动力学性能进行仿真计算，模型包括转向架模型、车体模型和轨道模型。

2.1 CRH2型动车组动力学模型描述

CRH2型转向架由构架、前后两个轮对、四个轴箱、制动装置、牵引拉杆以及弹性阻尼原件组成。进行系统动力分析的关键是部件自由度的确定和各部件之间自由度的选取。最终建立的CRH2型转向架的动力学模型如图1所示。

图1 CRH2转向架动力学模型

根据车身的参数建立车体的模型，并施加正确的连接关系，得到车体的动力学模型。把车体和转向架的动力学模型进行装配，得到整车的动力学模型。CRH2型动车组的动力学模型如图2所示。

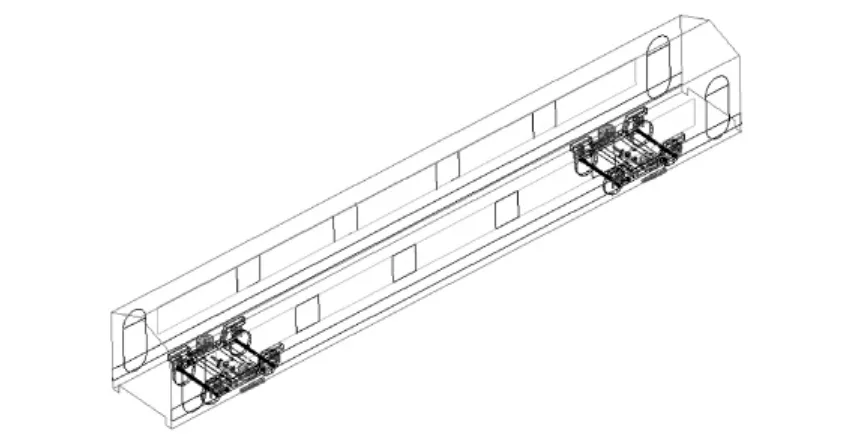
图2 CRH2整车动力学模型

2.2 模型的验证分析

将武广线不平顺数据输入模型，对以上建立的动力学模型进行试验验证，得到的仿真数据和测试数据的对比如图3所示。局部放大图如图4所示。取半径为4 500 m曲线上的检测数据进行曲线上动力学模型的验证，横向加速度的对比如图5所示。图中两条曲线的相关系数分别达到0.82，0.99，说明仿真计算是正确的，可以用来进行曲线上动力学性能的预测。

图3 仿真数据与实测数据的对比分析

图4 对比分析局部放大图

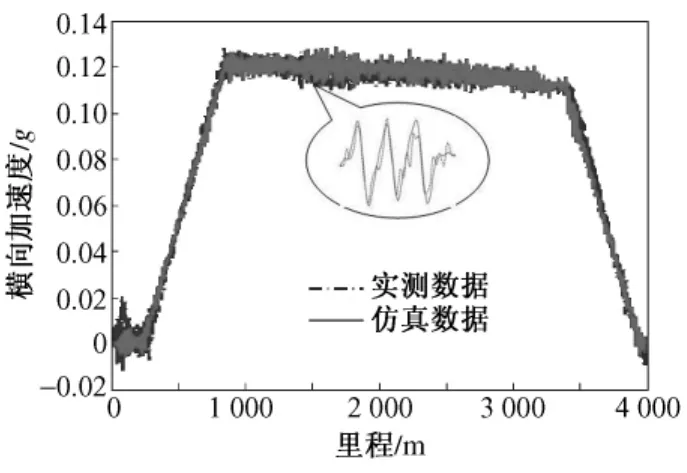
图5 曲线上车体横向加速度仿真值与实测值对比分析

3 曲线上动力学超限仿真实例及趋势分析

检测中心动检车在进行常规检测时，在某线路查出动力学指标超限多处。利用以上建立的检测列车的动力学模型，并输入超限处的实际路况，对超限原因进行分析。

3.1 动力学超限成因分析

取线路中发生轮轨横向力超限的典型位置，按照线路实际情况进行设置，并进行动力学仿真，得到轮对横向力随时间变化的曲线如图6。

图6 超限处横向力随里程变化的仿真曲线

由图6可以看出横向力最大值51.25 kN，发生在里程400～600 m之间。由仿真曲线可以看出，发生超限的地方，没有发生车辆的失稳、共振等现象，仅仅是车辆动力学响应的单点超限，因此，可以断定，该超限是由较大的轨道不平顺引起的。超限处轮轨的垂向力如图7所示。可知其最大值95.0 kN，最小值41.8 kN。可以看出，轮轨横向力超限处，对应一个较大的轮轨垂向力。其脱轨系数的变化如图8所示。可知脱轨系数的最大值为0.69，并没有超限，但该点仍有一个大值，说明在小半径曲线上，用轮轨横向力和脱轨系数控制车辆动力学响应是非常合理的。可以从车辆脱轨、破坏线路两个方面来防止危险工况的发生。

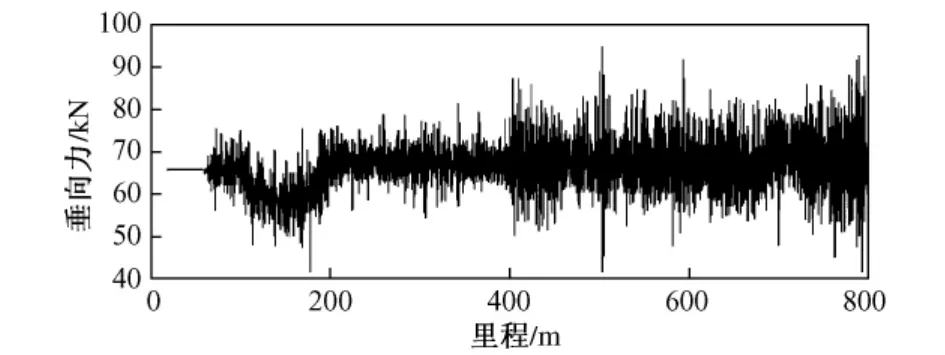
图7 超限处垂向力随里程变化的仿真曲线

图8 超限处脱轨系数随里程变化的仿真曲线

对某处的仿真结果进行深入处理，得到脱轨系数、轮对横向力以及接触点随里程变化的曲线分别如图9和图10所示。由图9和图10可知，动车组通过小半径曲线时，车轮踏面和轮缘同时与钢轨顶面和侧面接触，即两点接触;出现超限，轮轨两点接触，导致轮轴横向力变化剧烈，轮轴横向力和垂向力剧烈变化，导致轮轴横向力和脱轨系数指标超限。而这也是列车在小半径曲线上动力学超限的主要原因。

图9 脱轨系数和接触点随里程变化曲线

图10 轮对横向力和接触点随里程变化曲线

改变不平顺幅值，对曲线和直线采用当量的不平顺，得到车体横向加速度随里程变化曲线如图11所示。其中震荡较大的部分为曲线段车辆的横向加速度。

由图11可知，幅值相当地不平顺，造成的车辆动力学响应的大小在曲线上和直线上区别明显，说明小半径曲线上的轨道不平顺更应该严格控制。

图11 脱轨系数随里程变化曲线

图12 脱轨系数随里程变化的仿真曲线(局部放大图)

3.2 动力学超限影响规律分析

取脱轨系数超限处，对不同的速度进行仿真，研究车速对脱轨系数最大值的影响。当列车以60 km/h和70 km/h通过该处时，其脱轨系数随里程变化的曲线局部放大图如图12所示。分别取仿真速度为50～90 km/h，得出脱轨系数随速度的变化，绘出脱轨系数的最大值随速度的变化曲线如图13所示。

图13 脱轨系数的最大值随速度的变化曲线

由图13可知，脱轨系数的最大值随速度的增加而增大，但速度从50 km/h变化到70 km/h时(该曲线的通过速度为70 km/h)，脱轨系数的最大值变化不明显。速度从70 km/h变化到90 km/h时，脱轨系数的最大值变化较快。这说明，当小半径曲线上发生动力学超限时，应严格控制车辆以不高于均衡速度的速度通过，但也不宜采用过低的速度通过，因为降速通过并不能有效地减少超限的发生。

在另一超限处，改变线路的不平顺的幅值，进行动力学仿真，不同不平顺幅值下，脱轨系数最大值随不平顺幅值的变化曲线如图14所示。

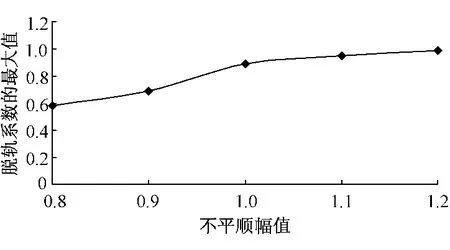
图14 脱轨系数最大值随不平顺幅值的变化曲线

由图14可知，脱轨系数的最大值随不平顺幅值的增加而增大较快。说明在小半径曲线上，不平顺的幅值对车辆动力学响应的影响较大。

在现行V≤120 km/h轨道不平顺管理标准，轨向三级超限为16 mm，在半径为600 m的曲线与直线上，各设置16 mm轨向不平顺，仿真得到脱轨系数如图15所示。前面的峰值为直线上的脱轨系数，后面的峰值为曲线上的脱轨系数，其最大值分别为0.64和0.78。可知，该标准在曲线上已经导致车辆的动态响应超限。车辆达到危险状态。

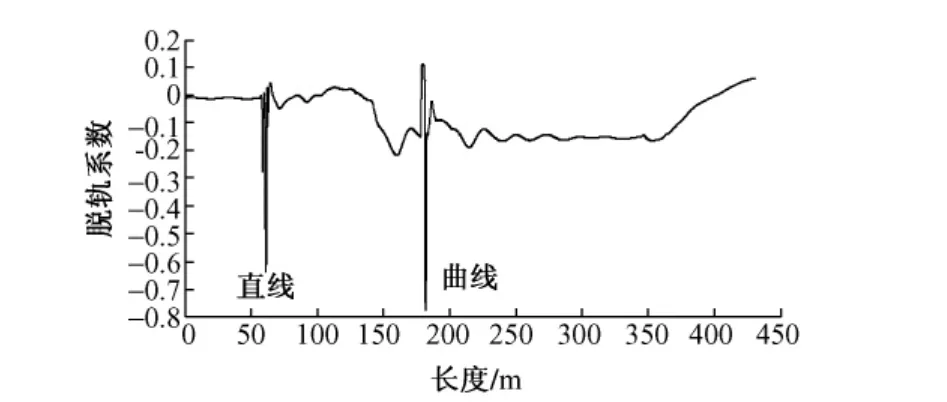
图15 16 mm不平顺幅值下脱轨系数

在轨向三级超限为16 mm条件下，绘制在不同半径的曲线上车辆以均衡速度通过时，车辆脱轨系数的变化曲线如图16所示。可知，在曲线半径 ＜600 m时，现行标准会导致车辆动力学响应超限。因此，在曲线半径＜600 m的小半径曲线，应更加严格地控制轨道几何不平顺。

图16 三级不平顺下不同速度对动力学响应的影响曲线

4 结论

本文基于虚拟样机技术对车辆的各个部件进行建模，并利用实测曲线、直线数据对车辆的模型进行了验证，验证结果良好，说明建立的模型是正确的，可以利用该模型进行动力学分析。

对曲线上的动力学超限进行了仿真分析，对曲线上产生动力学超限的影响因素进行了深入分析，分析结果表明:小半径曲线上车辆的动力学响应对轨道几何不平顺更加敏感，在轨道几何并未超限的情况下，也有可能发生动力学响应的超限。这是由于轮对的横移和摇头缩小了轮轨间的游间，增加了接触轮缘的几率，从而对轨道的几何不平顺更为敏感。

当小半径曲线上发生动力学超限时，应严格控制车辆以不高于均衡速度的速度通过，但也不宜采用过低的速度通过。

为保证曲线上车辆的动力学通过性能，在曲线半径＜600 m的小半径曲线上，应更加严格控制轨道几何不平顺，以保证行车安全。

［1］ 王福天．车辆系统动力学［M］．北京:中国铁道出版社，1994．

［2］ 李秋梅，张学利．快速线路曲线晃车的分析与整正［J］．铁道建筑，2005(11):79-81．

［3］ 全顺喜，王平，张海洋．曲线上钢轨横向位移影响因素分析［J］．铁道建筑，2010(2):114-116．

［4］ 翟婉明．国际铁道车辆系统动力学研究新进展［J］．铁道车辆，2004，42(1):1-6．

［5］ 曾庆元，向俊，周智辉，等．列车脱轨分析理论与应用［M］．长沙:中南大学出版社，2006．

［6］ 翟婉明．车辆—轨道耦合动力学［M］．北京:中国铁道出版社，2002．

［7］ GARG V K，DUKKIPATI R V．Dynamics of Railway Vehicle System，xiii ed．［M］．Toronto:Academic Press，1984．

［8］ 张卫华．机车车辆运行动态模拟研究［D］．成都:西南交通大学，1996．