桥上无缝线路附加伸缩力放散温度及区段的研究

2012-07-26谢铠泽张亚爽

铁道建筑 2012年11期

谢铠泽，王彪，张亚爽，王平

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031)

由于无缝线路长钢轨受到扣件和道床(有砟轨道结构)的约束，轨温变化会引起长钢轨中产生轴向温度力。轨温上升，产生轴向压力;轨温下降，产生轴向拉力。当无缝线路的固定区在桥上时，由于桥梁温度变化使梁发生伸缩，进而带动桥枕位移，桥枕位移使扣件产生纵向力，并作用于钢轨上，使钢轨受到由于梁的位移而产生的附加伸缩力［1］。夏天时由于温度高，桥上无缝线路不仅受到温度力，也受到附加伸缩力，这两种力会对桥上无缝线路安全运行产生很大影响，因此要对无缝线路进行应力放散。目前通常采用拧松扣件的方法使钢轨可以在一定程度上自由伸缩，钢轨纵向力得到释放，以减小梁轨的相互作用，但是尚无定量分析。本文对连续梁桥桥上无缝线路附加伸缩力放散温度及区段进行定量计算分析。

1 计算原理

桥上无缝线路的计算是基于梁轨相互作用原理［2-3］，取任意微段钢轨 dx，其受力平衡图式如图1所示。

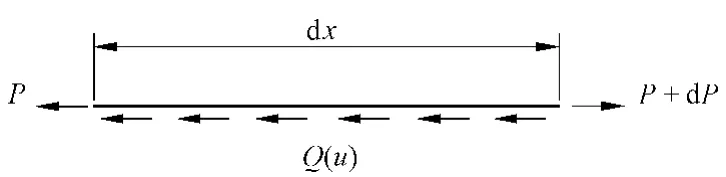
图1 梁轨相互作用原理

图1中，Q(u)为梁轨间发生相对位移时产生的摩阻力，u为梁轨间的相对位移，P为钢轨轴力，则有

在dx微段内钢轨的变形量dy为

式中，E为钢轨的弹性模量;F为钢轨截面面积;y为钢轨的纵向位移。

由式(1)和式(2)可得

因梁轨间的相对位移满足u=y－δ，δ为梁纵向位移，可以得到梁轨相对位移微分方程

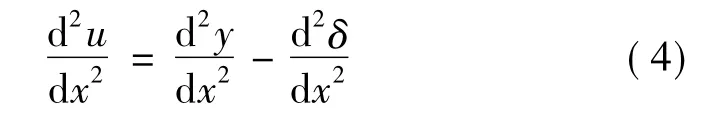
式(1)～式(4)即为梁轨相互作用原理的数学表达式，也是计算桥上无缝线路的基本方程。

2 计算方法

2.1 放散方式

主要研究两种放散条件:①桥梁直接升温至日最高温，然后进行附加伸缩力的放散;②在桥梁升温未达到当日最高温度时进行附加伸缩力的放散，之后桥梁继续升温至日最高温。通过对这两种放散条件进行比较，分析不同桥梁温度以及不同放散区长度对钢轨附加伸缩力释放的影响。

2.2 单元选取［4-5］

本文只分析钢轨和桥梁纵向的受力，不考虑桥梁墩台在温度变化作用下的影响，也不考虑钢轨和桥梁的扭转与弯曲，因此在ANSYS软件中选取杆单元模拟钢轨，选用梁单元模拟桥梁。

由于采用非线性弹簧单元能较好地模拟道床纵向阻力的实际情况，并且非线性弹簧可以实现放散时力的线性卸载，所以采用非线性弹簧单元模拟线路的纵向阻力。同时，在计算过程中模拟线路放散工况的步骤要用到线性弹簧。

2.3 模型处理

该模型的关键在于对非线性弹簧的两次处理。

①第一次处理:在模拟第1次桥梁升温时，先利用非线性弹簧计算得到桥梁升温的结果，计算出放散区非线性弹簧转化为线性弹簧的等效刚度，然后按线性弹簧计算，见图2。这样处理是因为非线性弹簧不能在模型计算中失效(模拟放散状态)，而线性弹簧可以。

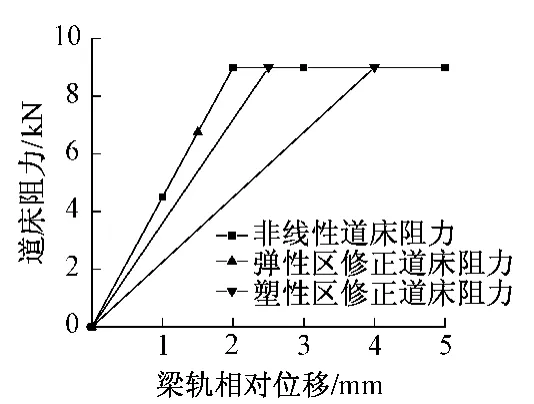
图2 弹簧线性等效刚度修正方法

②第二次处理:在桥梁温度未达到日最高温时进行附加伸缩力放散，之后还有一次桥梁升温过程，从而再次引起钢轨的附加伸缩力。对于第二次升温过程，需要对弹簧的位移—力对应关系进行重新模拟。举例说明:当附加伸缩力放散后的某弹簧所处的状态为弹性区段的某值时，其位移—力关系见图3(a)，处理后的位移—力关系见图3(b)。

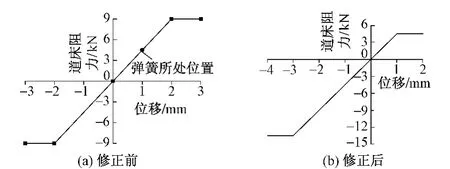
图3 弹簧位移—力关系

3 算例

选取主跨为(48+80+48)m的连续梁桥进行模拟，在连续梁桥两端各布置3×32 m简支梁，见图4。

3.1 模型的建立

模型中尽量减少边界条件对计算的影响，在桥梁边跨两侧分别取长100 m的路基，并取左侧路基左端点为坐标原点，建立线桥一体化模型［6-8］，见图5。

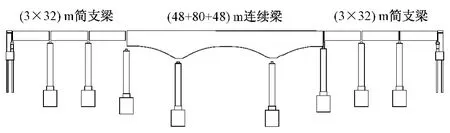
图4 桥梁布置

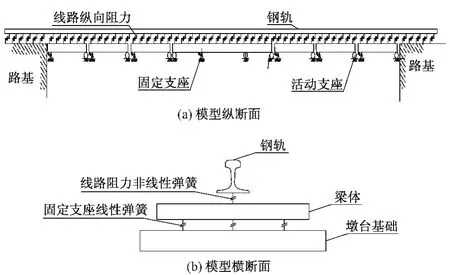
图5 桥上无缝线路附加伸缩力计算模型

3.2 计算参数的选取

规范规定:在计算混凝土桥上有砟轨道无缝线路附加伸缩力时，桥梁的温度变化为±15℃;对于简支梁桥台纵向水平线刚度，单线桥台不得小于1 500 kN/cm;对于单线跨度为32 m的简支梁桥墩顶水平线刚度不得小于200 kN/cm/线;对于连续梁桥墩水平线刚度取值为1 000 kN/cm/线［9-10］。

依据《跨区间无缝线路设计暂行规定》，在计算桥上无缝线路时，采用的道床纵向阻力为非线性的，见图6。

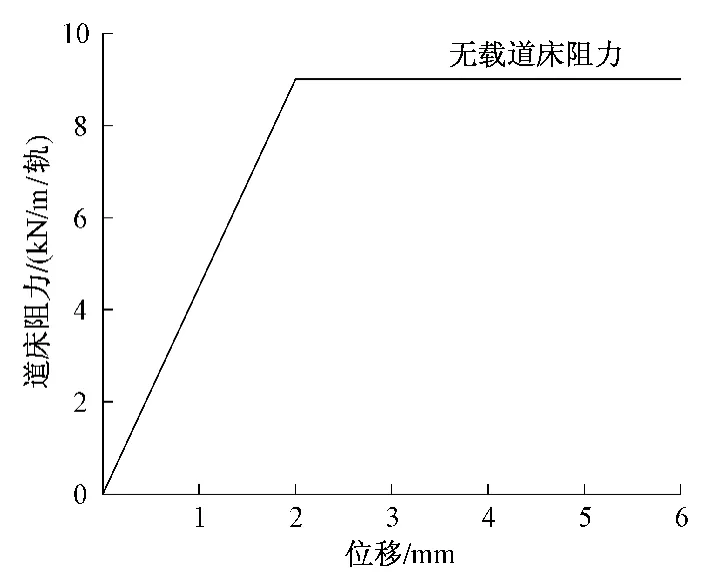
图6 有砟轨道道床纵向阻力

3.3 模型处理验证

对非线性弹簧的第一次处理进行验证:第1种模型是直接使桥梁升温15℃后放散，第2种是先使桥梁升温15℃，得到等效线性弹簧的刚度，然后重新建模。通过比较两种模型计算的钢轨附加伸缩力及梁轨相对位移进行验证。两种方法计算的钢轨附加伸缩力相对误差的平均值为1.08%，梁轨相对位移相对误差的平均值为0.96%，吻合得很好，因此这种处理弹簧单元的方法是可行的。

对非线性弹簧的第二次处理进行验证:第1种模型是直接使桥梁升温15℃，第2种模型是先使桥梁升温7.5℃，然后对非线性弹簧的刚度进行处理，再使桥梁升温7.5℃，并建立模型计算。通过比较两种模型的钢轨附加伸缩力及梁轨相对位移进行验证。两种方法计算的钢轨附加伸缩力相对误差的平均值为0.59%，梁轨相对位移相对误差的平均值为0.52%，吻合得很好，因此这种处理弹簧单元的方法也可行。

3.4 各种工况计算

对不同的工况分别计算最终钢轨的附加伸缩力，用于判别附加伸缩力放散时的温度以及放散的范围，具体的工况及模型模拟计算过程见表1。

表1 计算工况

各种工况的计算结果见图7～图10。

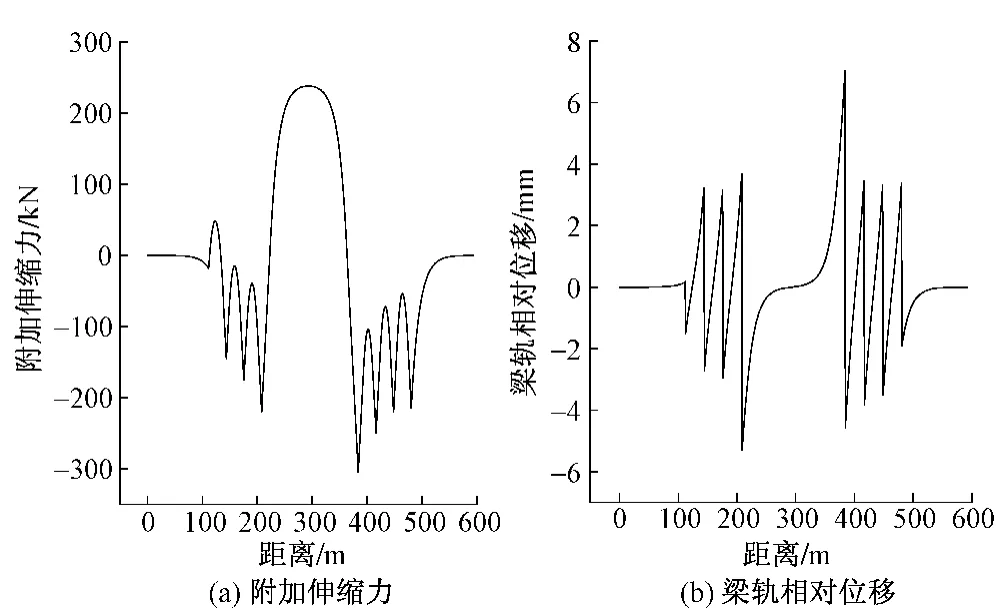
图7 桥梁直接升温15℃的计算结果

3.5 计算结果分析

1)将8种工况计算结果与直接升温15℃的钢轨附加伸缩力结果比较可知:8种工况均可降低钢轨的附加伸缩力，但是采取桥梁温度升高到日最高温时再进行附加伸缩力的放散取得的效果比较明显，而在桥梁温度未达到最高温度时进行附加伸缩力放散取得的效果不明显。同时也说明桥梁温度变化引起钢轨附加伸缩力的增加量比放散起的作用要大得多。从施工方面考虑，两种放散方式的劳动量相差不大，因此采用桥梁温度达到日最高温时进行放散的方式效果较好。

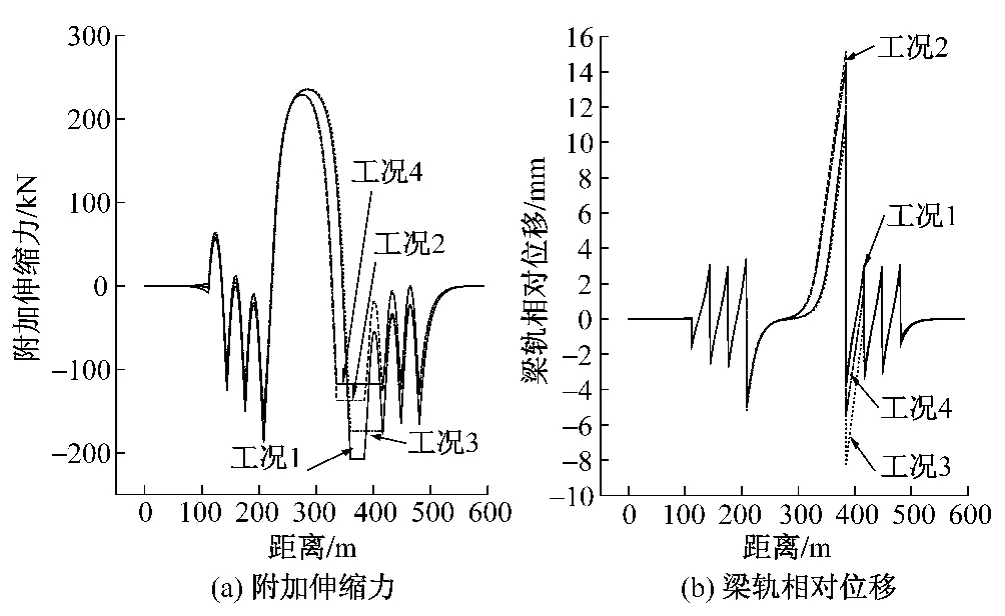
图8 工况1～工况4放散后的计算结果

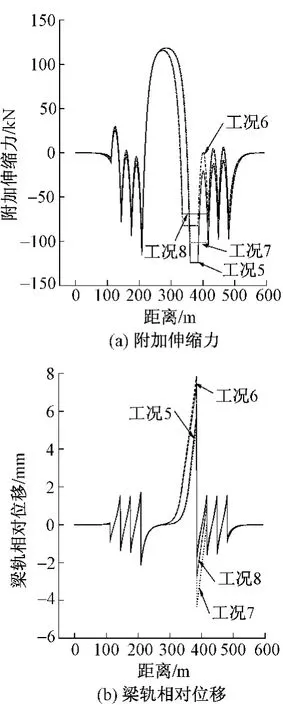
图9 工况5～工况8放散后的计算结果

2)比较工况1～工况4:放散后的钢轨附加伸缩力控制值并非随着放散长度的增加而降低，而是先降低后升高再降低。工况2及工况4放散后的钢轨附加伸缩力控制值不再在温度跨度最大的连续梁活动支座处，而是变成了在另外一侧的活动支座处，从图8中可知:原来位置处的钢轨附加伸缩力也是随着放散长度的增加而减小，说明连续梁温度跨度最大处活动支座对应钢轨附加伸缩力是随着该处附近的放散区段的长度的增加而减小，但是放散区段长度达到某值后继续增加就会使该桥上无缝线路附加伸缩力控制值的位置改变为连续梁对应的另一活动支座端，因此要想取得更好的效果就应该在对连续桥梁的一端进行附加伸缩力放散的同时，对另一端也进行适量的放散。工况5～工况8的附加伸缩力放散计算结果也反映了相同的规律。

图10 工况5～工况8放散后再次升温的计算结果

3)从图7～图10中梁轨相对位移数据可以验证放散理论的正确性，即通过允许梁轨发生相对位移减小梁轨相互作用，表现为钢轨的附加伸缩力降低，但梁轨相对位移增加了。对比工况1与工况2、工况3与工况4可知，随着放散区段长度的增加梁轨相对位移增加;比较工况1与工况3、工况2与工况4，梁轨相对位移随着放散区段的长度的增加而降低;这是由放散区段的位置决定的，由于工况3与工况4比工况1与工况2放散区段增加了邻近的一跨简支梁，而简支梁上的梁轨相互作用减弱，可以允许钢轨有一定的伸缩量，则钢轨会向着连续梁方向伸长，同时连续梁上的放散区的钢轨也向着邻近的简支梁方向伸长，这样使得简支梁活动支座处的梁轨相对位移减小而不是增加。图10(b)数据也显示出这种规律。