多事件触发巨灾债券设计与定价研究:以中国台风债券为例
2012-07-26李永,范蓓,刘鹃
李 永,范 蓓,刘 鹃
(1.同济大学经济与管理学院,上海200092;2.南京紫金财产保险股份有限公司,南京210000)
一、引言
巨灾债券对巨灾风险损失补偿作用令人瞩目,可以有效增强一国应对巨灾风险损失补偿能力。自1990年代以来,被美国、欧盟、日本等发达经济体成功应用于防范和化解地震、飓风等自然灾害造成的财产损失(Froot,1999)[1]。传统巨灾债券通过设置单一“触发事件”(trigger event)将投资者收益与损失联系一起,实现了保险市场风险向资本市场的转移,解决了巨灾风险的非可保性问题,应用范围已逐步扩大到农业、核燃料泄露、流行病、恐怖事件等非常规风险防范中(Bowers,2004;Lee,2004)[2-3]。但是由于巨灾造成的后果往往多方面,具有多样性、立体性特征,基于单一触发事件的巨灾债券已经难以满足市场多样化需求。因而多事件触发巨灾债券开始出现,其中,瑞士、美国、法国等都已相继发行了多事件触发巨灾债券,如地震飓风债券、恐怖袭击债券、体育赛程取消债券等。
巨灾债券定价是研究核心与难点之一,始于1990年代中期,仍然处于发展之中。定价新模型不断涌现,又很快被改进。早期 Cummins等(1995)[4]利用无风险套利思想讨论了巨灾衍生产品定价,将B-S理论应用于保险衍生品市场。Briys(1997)[5]在市场完全、巨灾损失指数服从几何布朗运动以及市场无套利机会等假设下,得出巨灾债券价格的表达式。Loubergé等(1999)[6]以B-S模型为基础,假设利率是连续变动下建立了巨灾债券定价模型。Morton Lane等(2000,2007)[7-8]对已发行的巨灾债券的参数进行回归分析,不断发展和完善了LFC巨灾债券定价模型。Pederson 和 Cox(1994,2000)[9,10]研究了均衡定价原理与普通无套利定价原理的关系,认为不完全市场背景下,不确定性现金收益的定价问题可以视为委托代理问题,而借助定价内核(pricing kernel)和等价鞅(martingale)技术可以将风险中性理论泛化到各种衍生品,拓展了巨灾债券的定价方法。Wang(2004)[11]通过概率变换发展了LFC模型,提高了计算效率。Woo(2004)[12]较早提出了多事件触发思想,认为现代巨灾风险如恐怖袭击风险面临的风险具有模糊性(ambiguity),多事件证券化产品则可以转移此类风险。由于牵涉“多事件”,定价过程比之以往更为复杂,实证研究直到Reshetar(2008)[13]出现,他以巨灾保险财产损失、死亡人数为触发事件,对英国巨灾债券债券价格进行了估算。至今相关研究仍显不足,滞后于实践发展速度与需要。国内研究仅限于普通巨灾债券的研究,尚未开展多事件触发巨灾债券的探索。代表性成果包括韩天雄等(2003)[14]、田玲等(2006)[15]、施 建 祥 (2006)[16]、张 庆 洪 等(2008)[17]、李永等(2005,2010)[18-19]。事实上,相比普通巨灾债券,多事件触发事件巨灾债券具有投资风险低、违约概率低、信用评级高等优势,较易为市场接纳等优势,更适合在类似中国的新兴市场推行。
本文以多事件触发巨灾债券为研究对象,构建并阐述了产品定价模型及其实现过程,首次在中国台风巨灾财产损失、受灾面积两事件基础上,完成对巨灾债券的初步设计与价格估算。具体而言,考虑多事件结构的巨灾债券运行机制和市场的不完全性,建立委托代理定价模型;对中国1990年以来历次台风直接经济损失和受灾面积的边缘分布分别进行拟合;通过Copula函数建立边缘分布的联合分布比较分析,确定了Clayton Copula概率分布函数,完成了定价分析。
二、运作与定价模型
(一)运作原理
本文以付息巨灾债券为例。每年末按合同约定条件向投资者支付息票,收益来自于息票利息和期末本金两部分,利息和本金均不确定,即都存在“违约”可能;以台风巨灾直接经济损失、受灾面积作为标的损失指标,当且仅当一项标的损失超过触发水平,当期和余期的息票将不予支付(或按一定比例支付);当且仅当两项标的损失均超过各自对应触发水平,到期的本金也将不予偿还。即:
1.到期日为T,面值为F,每年支付息票利息为 Ct,t=1,2,… ,T,息票和本金均不确定,取决于触发事件是否发生;
2.单位直接经济损失额为IL=ItL,0≤t≤T,为非负随机变量服从FL分布;
3.单位受灾面积 IS=,0≤t≤T,为非负随机变量服从FS分布;
5.触发事件的起始时间:
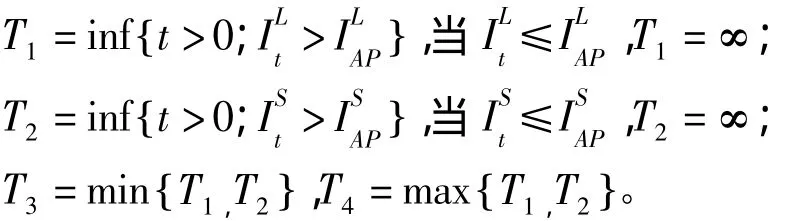
6. 一期利率 {r(k);k=0,1,2,…,T-1}。投资者第k年的现金流收益表示为:
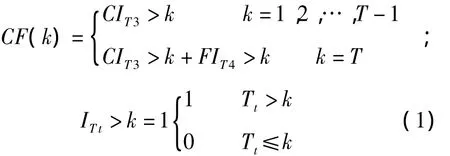
(二)定价模型
巨灾债券是一种零贝塔产品,即与金融市场其他产品价格收益相关性几乎为零,无法借助资产组合实现定价过程(Litzenberger,1996)[20]。实际上,巨灾债券收益取决于巨灾发生概率,而在不完全性的巨灾债券市场,并不存在可以套期保值的交易性损失指数。通过委托代理定价模型(representative agent pricing model)可以较合理解决巨灾债券市场的不完全性问题。
假设金融市场变量的概率空间(Ω(1),p(1),P1),影响巨灾债券定价相关金融市场变量包括利率期限结构等因素;巨灾风险变量的概率空间(Ω(2),p(2),P2),P2概率由巨灾事件概率决定。整体模型的概率空间X(Ω,p,P),假设决定经济风险变量与巨灾风险变量的事件相互独立,则Ω=Ω(1)×Ω(2),p=p(1)×p(2),P=P(1)×P(2)。代理人根据效用最大化进行消费决策,实现未来现金流收益 CF={CF(k);k=1,2,…,T}:
当T=0时价格期望值:
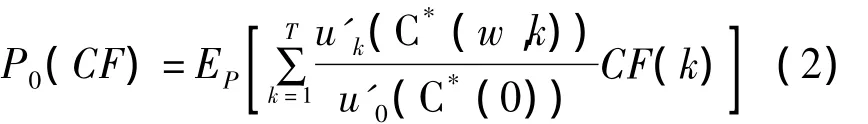
其中,C*(k);k=0,1,2,…,T 表示累积消费的随机过程;uk(C*(w,k))表示在k期随机经济状态为w时效用水平。
假设完全市场与无套利定价理论成立,一期利率为:
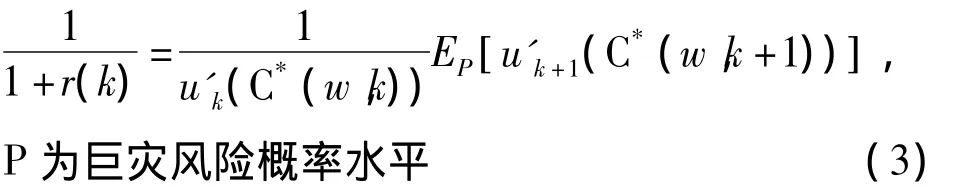
则价格期望值转换为:
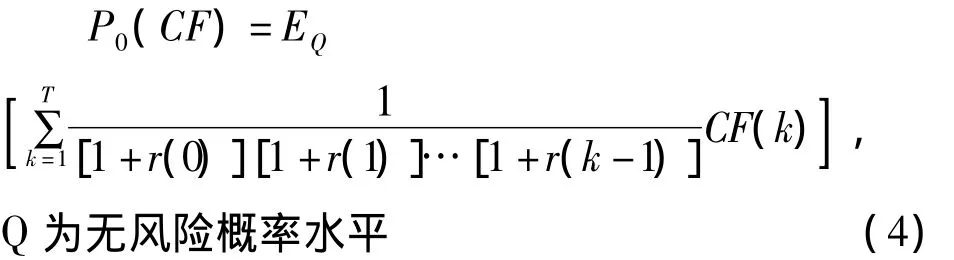
通过求Radon-Nikodym①在[0,T]区间Radon-Nikodym导数:[1+r(0)][1+r(1)]…[1+r(k-1)导数,证明巨灾风险债券存在定价内核或折价因子。进一步借助等价鞅原理证明式(2)等于式(4)[10],因此可将均衡定价模型的巨灾债券定价过程转化为普通无套利定价和概率结构两个阶段,即式(4)所示价格由现金流收益和利率期限结构两部分组成。假设利率为依赖金融风险大小而独立于巨灾风险的变量;现金流收益CF(k)只与巨灾风险有关。相对于单一触发性质债券,多事件触发巨灾债券价格的概率结构更为复杂,其价格表示为:
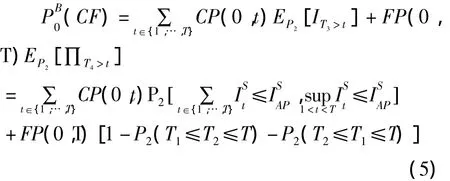
其中,P(0,k)表示k时到期,面值为1元的无违约零息债券在t=0时价格。
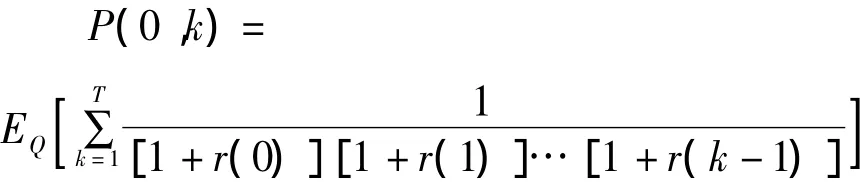
三、参数估计与实证结果
(一)数据处理
选取1990-2009年《中国气象灾害年鉴》记录的131次台风灾害的直接经济损失、受灾面积数据为随机变量样本数据;通过CPI指数逆推法将各年直接经济损失额换算为2009年不变价,并对受灾面积剔除0值。
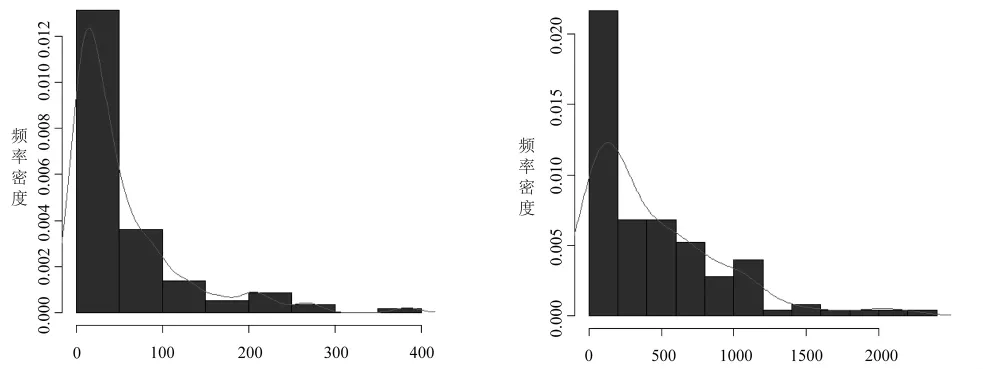
图1 直接经济损失、受灾面积的统计密度直方图
根据中国台风直接经济损失、受灾面积的样本数据,绘制频率密度直方图和密度估计曲线:均具有非对称性和重尾特征,其中直接经济损失样本数据偏度为2.207515,分布为左偏斜,峰度5.754364,数据集中于单侧极端,尾部分散;受灾面积样本数据偏度为1.511036,峰度2.460155,分布也呈现左偏斜,尾部分散(见图1)。
(二)边缘分布检验
假设直接经济损失、受灾面积为连续型变量。选取6种常用概率分布函数:帕累托分布、伽马分布、对数正态分布、偏斜正态分布、指数分布、威布尔分布,采用极大似然法估计参数,借助Kolmogorov-Smirnov(K-S)法进行拟合优度检验,确定最适概率分布函数。见表1、表2。
在直接经济损失边缘分布结果中,伽马分布拟合优度检验效果最好。K-S检验在5%显著性水平D=0.0733,P值 =0.6858 >0.05。确定伽马分布Gamma(0.7880,69.4444)为直接经济损失的统计分布(见图2),概率密度函数为:
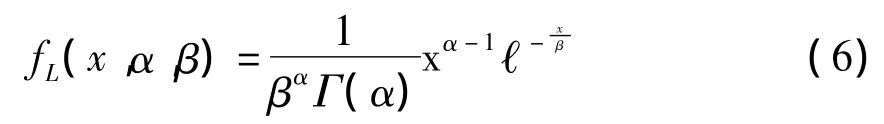
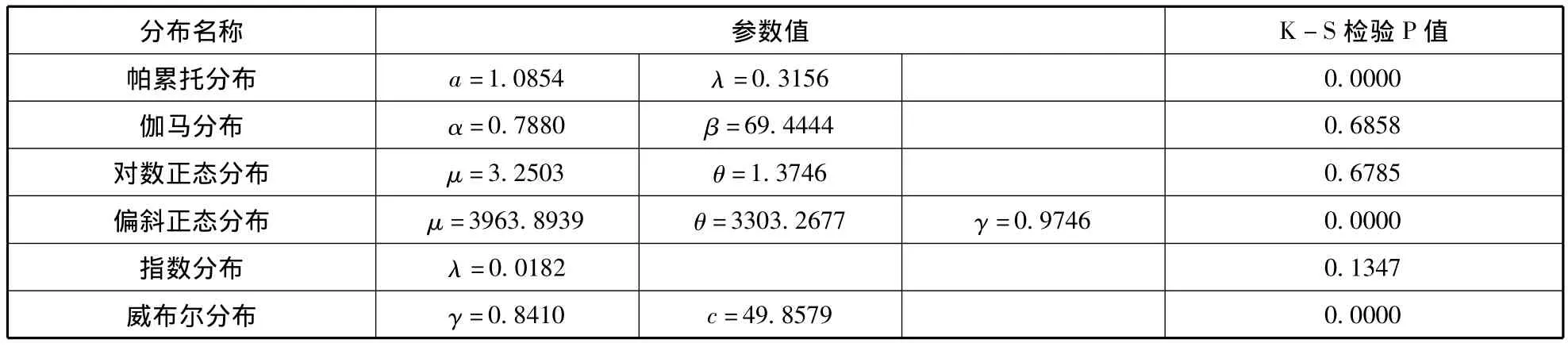
表1 直接经济损失的6种概率分布拟合结果
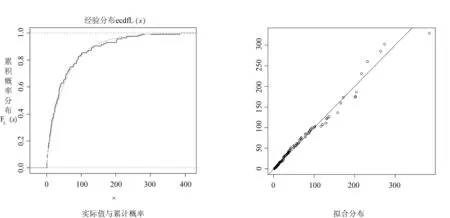
图2 中国台风直接经济损失分布拟合结果
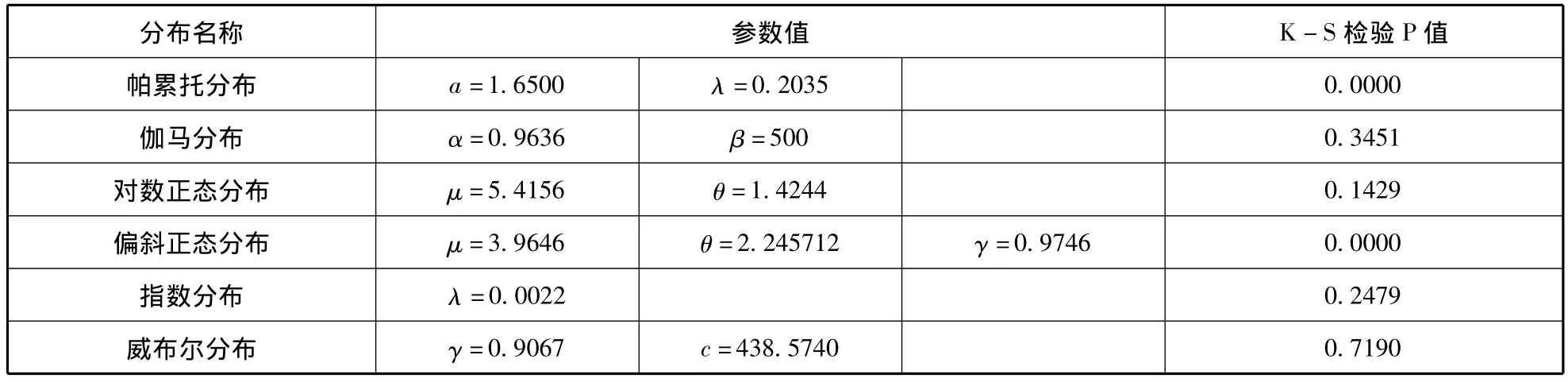
表2 受灾面积的6种概率分布拟合结果
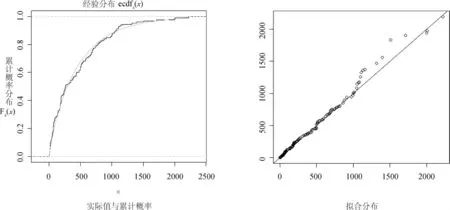
图3 中国台风受灾面积分布拟合结果
在受灾面积边缘分布拟合结果中,威布尔分布拟合优度检验效果最好。K-S检验表明在5%显著性水平D=0.0622,P值=0.7190>0.05。因此,确定威布尔分布Weibull(0.9067,438.5740)为受灾面积的统计分布(见图3),其概率密度函数为:
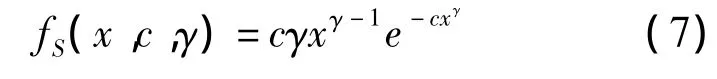
(三)联合分布函数与参数估计
1.Copula函数
由于通常直接经济损失、受灾面积具有较强相关性,不能视作相互独立变量。而在定价过程中现金流收益取决于二维随机变量经济损失、受灾面积概率函数形式,所以需要构造二者联合分布函数。可采用阿基米德Copula连接函数①Copula概念最先被Sklar(1973)[21]引入用于连接联合分布与它们各自的边缘分布,Mendes等(2004)[22]将其延伸到金融风险分析用于测度金融资产之间的相依结构。阿基米德Copula函数可以较好捕捉变量间非对称相关关系和尾部相关性特征,在金融和保险分析中广泛应用。拟合解决这一问题,即:
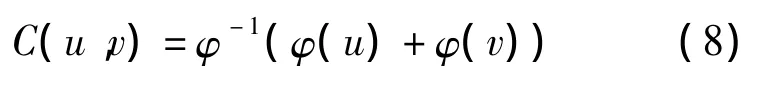
其中,φ(·)表示生成元,Gumbel、Clayton 和Frank Copula函数为常见二元阿基米德Copula函数形式。
2.非参数估计
根据Kendall秩②Kendall秩相关系数,表示随机向量之间一致概率与不一致概率之差,即:τ(X1,X2)=P{[X1-E(X1)]-[X2-E(X2)]>0}-P{[X1-E(X1)]-[X2-E(X2)]<0}。与阿基米德Copula生成元参数间关系,结合K-S方法进行参数估计和拟合优度检验。通过计算得到Kendall秩相关系数τ=0.6795,以及 Copula参数 θ的 Kendall秩估计结果。见表3。

表3 Copula参数θ的Kendall秩估计结果
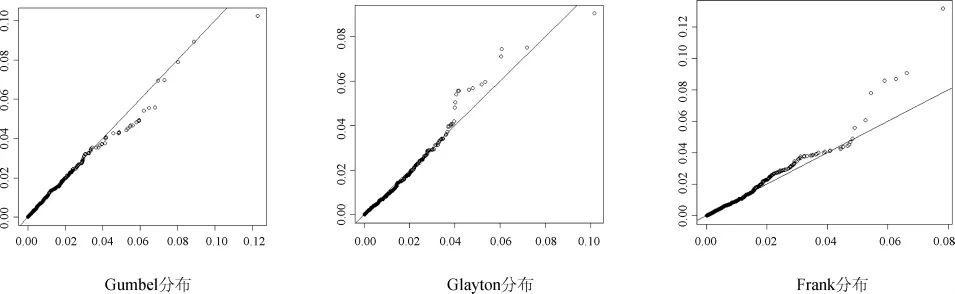
图4 阿基米德Copula联合分布函数拟合结果
3.联合分布函数选择
对比 K-S和 Copula拟合优度检验结果,Clayton Copula函数拟合情况最好(见图4)。根据生成元,得到联合分布的累计概率函数:
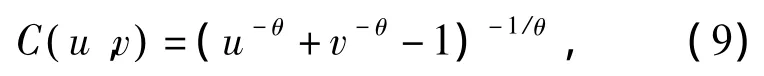
其中:

(四)数据设定与定价分析
1.数据设定与定价
假设其他基本数据设定:
(1)本金为100元,息票率为300个基点的1年期债券,即 F=100,C=3,T=1;
(2)市场利率参照2011年7月5日的12个月中国银行同业拆借利率(SHIBOR),r(0)=5.15%,并假设利率在到期前保持不变;
由式(9)计算触发事件发生概率,由于第一类触发事件即损失标的有且仅有一件超出触发水平造成债券利息违约的概率为28.16%;由于第二类触发事件即损失标的均超出触发水平造成本金违约的概率为11.13%。已知定价公式表示为:
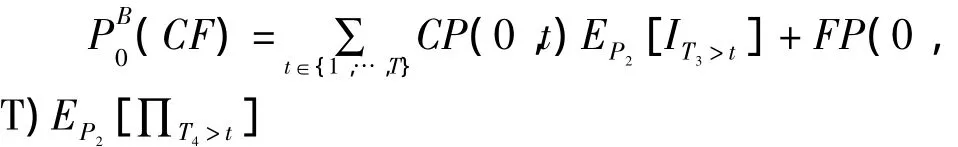
根据中性定价公式可知1年期债券息票的价格期望为2.05,本金的价格期望为84.52,所以该多事件触发台风巨灾债券价格=2.05+84.52=86.57元。
2.价格动态分析
(1)价格敏感性分析
分别分析定价模型中主要参数变化对价格的影响程度,着重考察巨灾风险变量即双损失标的的触发值增减10%时价格变化(见表4);金融市场变量即市场利率与债券息票率分别增减10%时价格变化。见表5。
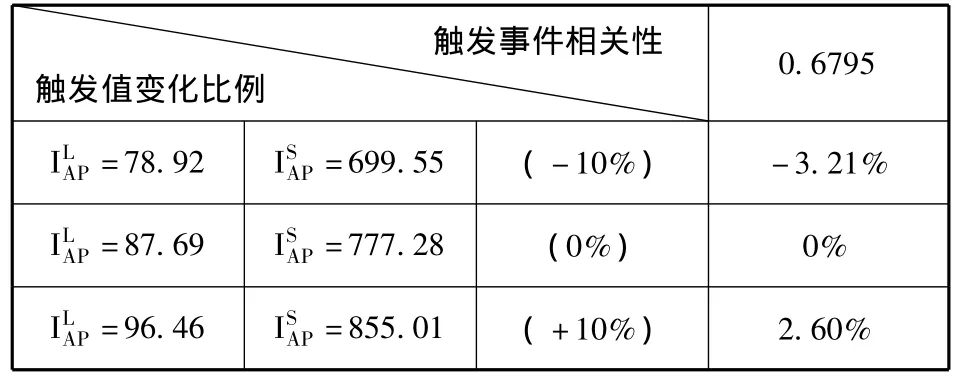
表4 损失标的触发值对价格的敏感性
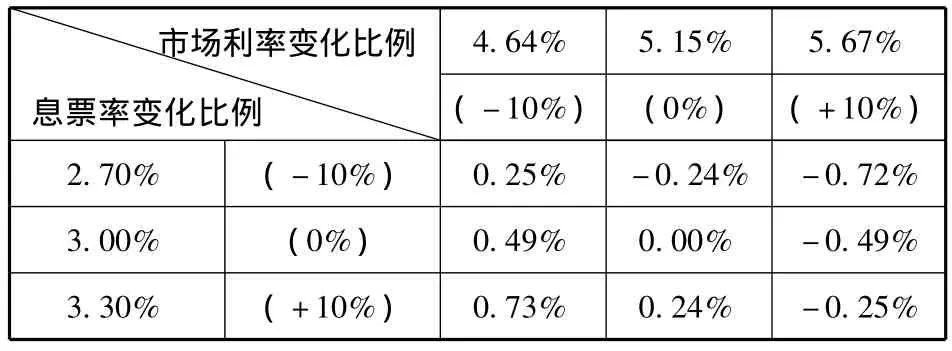
表5 息票率与市场利率变化比例对价格的敏感性
第一,巨灾风险变量中,债券价格与触发值的变化正相关,即触发值增大导致现金流损失的可能性下降,风险收益率低导致债券价格高。
第二,金融市场变量中,债券价格与市场利率的变化负相关,与息票率的变化正相关,而且对市场利率的变化更敏感。债券价格和市场利率的关系与债券定价理论是吻合的,对息票支付债券而言,息票率增加,会增加债券的现金流,从而提升债券价格,反之亦然。此外,该结论还表明,在金融市场价格波动风险主要来自于市场利率。
第三,相较对金融市场变量的敏感度,债券价格对巨灾风险变量更加敏感。通过初步比较,表4价格的变化比例大于表5价格变化比例。以市场利率和触发值两个变量为例,将基础情况τ=0.6795=87.69=777.28作为参照点,模型其他参数不变,当市场利率分别增加10%和减少10%,价格变化分别为0.487%和0.492%,而当双触发值分别增加10%和减少10%,价格变化分别为3.21%和2.6%。可见,对比普通巨灾债券,多事件触发的台风债券虽然违约风险较低,更加接近普通债券,但价格变化对巨灾风险因素更加敏感。
(2)价格稳定性分析
价格稳定性分析研究使债券价格趋于不变的参数水平,着重考察了损失标的中直接经济损失的触发值。见表6。
四、结论
近年来,中国自然灾害造成的经济损失愈发严重,巨灾风险补偿工作迫切需要从传统的计划模式向市场模式转变。在这一转变过程中,保险作为社会稳定器,发挥化解巨灾风险和损失补偿的功能,是不可替代的。长期以来,主要依靠政府的赈灾资金灾与民间援助,但可谓杯水车薪。而由于中国保险发展正处于初级阶段,覆盖率低、偿付能力不足等现象严重制约着巨灾保险市场的发展,未能充分体现对经济风险的规避功能。当前巨灾债券等保险衍生产品正在发挥着重要作用,可作为传统再保险的补充手段,不仅使相关者获得制度创新条件下的报酬递增和自我强化利益,而且可能成为中国巨灾补偿制度完善的方向之一。
基于以上讨论,本研究可以对中国巨灾债券的理论与实践发展起到一定推动作用。得到主要结论如下:
(1)巨灾债券的价格随着触发值的增加而增加。主要原因在于,损失触发值的增加表明该债券是易触发、高风险的,即由违约风险引起的风险溢价较大,所以收益率也偏大。上述因素与风险溢价产生联系,进而影响债券价格。另外,债券价格和市场利率的关系与债券定价理论是吻合的,债券价格随着市场利率的增加而减少,随着息票率的增加而增加。

表6 直接经济损失触发值变化对价格的稳定性
(2)在巨灾债券设计时,我们可以考虑通过增加触发值来达到在价格稳定前提下巨灾风险保障的目的,尤其可以应用于极端事件如核燃料泄漏、流行病、恐怖事件等的防范之中,并且可以满足愿意承担较低风险,支付较高价格的投资者。
(3)与金融市场变量的敏感性相比,价格变化过程中巨灾风险变量发挥主要作用。按照理论预期,多事件触发巨灾风险债券由于现金流损失的可能性很小,更接近于普通债券,应与金融市场变量的相关性较强。此结论有悖于理论的原因可能是本文台风债券所选择的触发事件相关性为0.6795,独立性较低。所以在多事件结构的巨灾债券设计时,可以考虑选择除受灾面积外,其他与经济损失标的事件相关性较低的事件,如死亡人数,从而减少触发事件的相关性来降低价格变动中巨灾风险因素的作用,同时也有利于应对灾害的异质性结果。
本文实现了对多事件触发的巨灾债券定价模型与应用研究的初步探讨,但研究中仍然有如下方面需要考虑并解决:要将多事件触发的台风巨灾债券定价推广到其他巨灾风险,建立涵盖自然灾难和人为灾难的多风险结构产品的定价模型;债券期限结构复杂化,要将设计期限延长使分析过程更具有普遍意义;等。上述问题的存在,也为今后研究的完善明确了方向。
[1]Froot K A.The Financing of Catastrophe Risk[M].Chicago:University of Chicago Press,1999.
[2]Bowers B.Old Cat-New Tricks[J].Best's Review,June 2004:45-52.
[3]Lee M.Securitizing Terrorism Risk Could Be Next[J].Best's Review,June 2004:48.
[4]Cummins J D.Geman H.Pricing Catastrophe Insurance Futures and Call Spread:An Arbitrage Approach [J].Journal of Fixed Income,1995,(4):46-57.
[5]Briys E.From Genoa to Kobe:Natural Hazards,Insurance Risks and The Pricing of Insurance-Linked Bonds[M].London:Lehman Brothers International,1997.
[6]Loubergé H,Kellezi E,Gilli M.Using Catastrophe-Linked Securities to Diversify Insurance Risk:A Financial Analysis of CAT Bonds[EB].University of Geneva Working Paper,1999,22(2):125-146.
[7]Morton N L.Price Risk and Ratings for Insurance-Linked Notes:in Your Portfolio[R].USA:Sedgwick Lane Financial,LLC,1998.
[8]Morton N L.Pricing Risk Transactions[R].USA:Lane Financial,LLC ,2000.
[9]Pederson.H.Some Aspects of the Martingale Approach to the Term Structure of Interest Rates[C].In Proceedings of the 4th International AFIR Colloquium,1994,(2):567-587.
[10]Cox S,Pederson H.Catastrophe Risk Bonds[J].North American Actuarial Journal,2000,4(4):56-62.
[11]Wang S S.Cat Bond Pricing Using Probability Transforms[C].Geneva Association.Insurance and the State of the Art in Cat Bond Pricing.Working Paper Series,2004:278.
[12]Woo G.A Catastrophe Bond Niche:Multiple Event Risk[EB].NBER Insurance Group Workshop,Cambridge,2004.
[13]Reshetar G.Pricing of Multiple-Event Coupon Paying CAT Bond [EB].Swiss Banking Institute,February,2008.
[14]韩天雄,陈建华.巨灾风险证券化产品的定价问题[J]. 保险研究,2003,(12):31-33.
[15]田 玲,向 飞.基于风险定价框架的巨灾债券定价模型比较研究[J].武汉大学学报(哲学科学版),2006,(2):168-174.
[16]施建详,我国巨灾保险风险证券化研究一台风灾害债券的设计[J]. 金融研究,2006,(5):103-112.
[17]张庆洪,葛良骥.厚尾稳定分布巨灾风险的集合分散效应[J]. 统计与决策,2008,(3):29-33.
[18]李 永.我国地震巨灾风险证券化的实证分析[J].华北地震科学,2005,(4):47-51.
[19]李 永,刘 鹃.基于无套利利率模型的台风巨灾债券定价研究[J]. 预测,2010,(1):49-53.
[20]Litzenberger R H Beaglehole D R,Reynolds C E.Assessing Catastrophe Reinsurance-linked Securities as A New Asset Class[J].Journal of Portfolio Management,1996,(23):76-86.
[21]Sklar A.Random Variables:Joint Distribution Functions and Copulas[J].Kybernetika,1973,9(6):449-460.
[22]Mendes B.Measuring Financial Risks with Copulas[J].International Review of Financial Analysis,2004,13(13):27-45.
