UCT－RAVE算法在多人非完备信息博弈中的应用

芮雄星，王一莉

（南京工业大学 电子与信息工程学院，江苏 南京210009）

0 引 言

完备信息博弈和非完备信息博弈是机器博弈的两个分支，对于完备信息博弈，国内外已经取得了的很多较好的研究成果。而非完备信息博弈领域的相关研究还不十分成熟，目前为止非完备信息下很成功的人工智能博弈程序还很少。传统的基于最小最大 （minimax）搜索的算法很难适用于多人非完备信息博弈，由于每个博弈者可能使用不同的博弈策略，很难找到一个静态评价函数能够很好的应对每种博弈策略；而非完备信息的存在导致不确定博弈行为大量增加，博弈搜索空间将变得庞大［1］。而且，alpha－beta剪枝在多人博弈中效率很低，虽然在二人完备信息博弈中alpha－beta剪枝能使空间复杂度从O（bd）降为O（bd/2），但在多人博弈中，最好的情况只能使空间复杂度降为，其中n为玩家人数［2］。本文将介绍一种新的博弈 搜 索 算 法 UCT－RAVE［3－4］。 并 通 过 与 蒙 特 卡 罗 抽 样（Monte－Carlo sampling）技术［5］相结合，将其应用于多人非完备信息博弈中。通过简单的三人争上游牌类博弈实例，验证此方法的可行性和有效性；并与UCT算法比较，测试其性能。

1 UCT－RAVE介绍

UCT－RAVE是应用于树搜索的上限置信区间 （upper confidence bound applied to tree search）方法和快速动作值估计 （rapid action value estimation）方法的结合，是结合蒙特卡罗 （Monte－Carlo）搜索方法和强化学习 （reinforcement learning）方法为一体的一种博弈搜索算法，由Sylvain应用在计算机围棋上获得了巨大的成功［6］。

1.1 UCT介绍

UCT （UCB applied to TRee）是利用UCB （upper confidence bound）公式和蒙特卡罗模拟的结果来增量扩展搜索状态的一种算法。UCB是为了解决K臂赌博机问题［7］而产生的，K臂赌博机是一种假想的具有K只手柄的老虎机，可做的动作是选择并拉下其中的一只手柄，而由此所赢取的一定数量的钱就是和这个手柄 （动作）相关联的收益（reward）。问题是如何根据当前已经掌握的每只手柄的收益情况决定下次拉下哪知手柄，一般来说，玩家会根据当前所积累的知识来做决定，这称之为开发 （exploitation）。如果一味的选择已开发过的手柄，而不尝试其它的手柄，则可能会错过收益率更高的手柄，因此应当适度地尝试未开发过的手柄，这称之为探索 （exploration）。UCB试图解决开发与探索之间的矛盾，寻找开发与探索之间的平衡点［8］。

UCB利用当前掌握的知识加上一个调整项来平衡开发与探索之间的矛盾。在每次做出选择时，UCB根据每只手柄到目前为止的平均收益值，加上调整项的值，得出本次选择此手柄的UCB值，挑选拥有最大UCB值的手柄作为本次所要选择的手柄。UCB公式表示如下

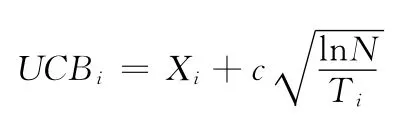
式中：UCBi——第i只手柄经由UCB公式运算后所得到的值，Xi——第i只手柄到目前为止的平均收益值，Ti——第i只手柄被选择的次数，N——到目前为止所有手柄选择次数的总和。公式中前项即为此手柄的过去表现，即开发项，后项则是调整值，即探索项。其中调整项值会随这只手柄被选择次数的增加而减少，以便选择手柄时，不过分拘泥于旧有的表现，适当探索其它手柄。从而在开发和探索之间进行平衡。

UCT把每一个节点都当作是一个K臂赌博机问题［9－10］，而此节点的每一个分支，都是K臂赌博机的一只手柄。选择分支，就会获得相对应的收益，对于博弈而言，UCB公式的收益值就等于该状态下的胜率，而该胜率是按照蒙特卡罗抽样的概念，用模拟博弈的结果来决定。所谓的模拟博弈，就是给定一个局面 （在此给的是叶节点所代表的局面），由计算机接手博弈，直到终局，然后判定并回传胜负结果。UCT会据此结果，更新叶节点到根节点路径上所有节点的收益值。可以用状态动作对 （s，a）的方式来表示UCT收益公式

式中：n（s，a）——s状态下a动作被选择的次数，n（s）——s状态被访问的次数，而选择动作的策略πUCT（s）就是使平均收益最大化：。

1.2 RAVE介绍

RAVE （rapid action value estimation）［11］是基于值 （valuebased）函数的强化学习思想在UCT方法中的应用。RAVE收集并评价UCT搜索中产生的状态动作对，并在下一次UCT搜索时加以引导，使UCT能够更多的搜索更好的分支。

强化学习是一种无监督的机器学习方法，它被称之为“和批评者一起学习”。批评者 （critic）并不反馈应该做什么，而仅仅反馈之前所做的怎么样12。最典型的强化学习算法是Q学习算法，可以看作是马尔可夫决策过程（Markov decision processes）的一种变化形式。

马尔可夫决策过程是强化学习的数学模型，它是由四元组组成：＜S，A，R，T＞，其中S是离散的状态集，A是离散的动作集，R：S×A→R是奖励函数，T：S×A→PD（S）是状态转移函数，PD（S）是状态集S上的概率分布函数。

典型的基于折扣报酬的强化学习问题通常可以描述为给定＜S，A，R，T＞，寻找策略π使得期望折扣报酬总和最大

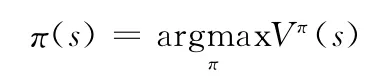
式中：Vπ（s）——折算累积回报，上式可以改写为

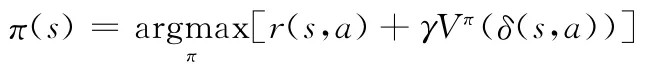
式中：r（s，a）——s状态下执行a所得的报酬值，γ是折扣因子。

定义Q（s，a）为从状态s开始并使用a作为第一个动作时的最大折算累积回报，换言之，Q的值为从状态s执行动作a的立即回报加上以后遵循最优策略的值

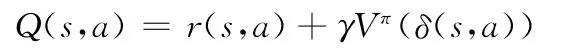
则

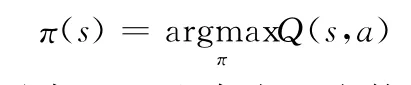
动态规划理论保证至少存在一个策略π＊使得对任意s∈S有

值函数Q（s，a）的估计有很多种算法，比如TD（λ）［13］。如果环境模型是已知的或是可学习的，那么基于值函数的强化学习算法可用于基于样本的搜索。可从模型中抽样来获得模拟场景，通过模拟经验来更新值函数。

RAVE是基于值函数Q（s，a）的强化学习方法，通过基于样本的搜索树来动态更新值函数。为了与UCT相结合，RAVE的收益公式定义为

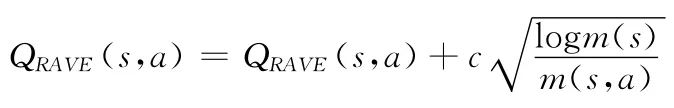
式中：m（s，a）——s状态下a动作被选择的次数，m（s）——s状态被访问的次数。

1.3 UCT和RAVE结合

UCT需要对每个s∈S状态下可供选择的动作进行抽样，以便比较各分支的收益情况并做出路径选择。如果动作空间巨大，可供选择的分支数就很多，要用足够多的模拟次数来区分分支的好坏［14－15］，而巨大的模拟次数将影响算法的性能。为减少模拟次数，UCT中加入在线学习知识RAVE，将RAVE值作为分支选择的另一参考，以提高分支选择的准确性。引入线性因子β（s，a）把QUCT和QRAVE线性组合到一起

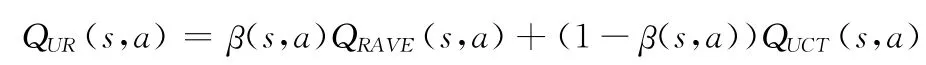
式中：k——平等因子，控制了QUCT和QRAVE所占的比重。同样选择动作的策略πUR（s）就是使平均收益最大化

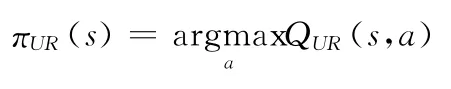
2 UCT－RAVE在非完备信息博弈中的应用

在非完备信息博弈中，博弈的真实状态是不可知的，比如牌类游戏中对手的牌是未知的，进行博弈的玩家所掌握的信息是不对称的和不完备的，这使得非完备信息博弈的研究更具有挑战性。为了应用UCT－RAVE算法，必须把这部分未知信息确定下来，可以通过猜测或计算等多种方法，而应用最广泛的是蒙特卡罗抽样方法。

2.1 蒙特卡罗抽样算法

蒙特卡罗方法又称为计算机随机模拟方法，是一种基于随机数的计算方法。它通过随机抽样将非完备信息博弈问题转换为完备信息博弈问题，同时通过大规模的抽样次数来逼近真实的情况。该方法在一些非完备信息博弈游戏中，例如Alberta的桥牌程序，已经取得了较好的效果。

2.2 UCT－RAVE与蒙特卡罗抽样相结合

UCT－RAVE算法运行过程中的两个重要因素在于节点的动态扩展和节点值的回溯运算。在非完备信息条件下，这两点是无法实现的。因此UCT－RAVE算法必须与可以将非完备信息条件转换为完备信息条件的蒙特卡罗抽样算法相结合。

UCT－RAVE与蒙特卡罗抽样算法的结合体现在搜索算法初始化过程中完备信息局面的生成。在UCT－RAVE算法进行一次搜索时，首先使用蒙特卡罗抽样算法对非完备信息局面进行抽样生成完备信息局面。然后UCT－RAVE算法依据这个完备信息局面进行一次搜索和节点的扩展。下次搜索将基于另一个蒙特卡罗抽样生成的完备信息局面，每次搜索所生成的节点都保存于同一棵搜索树中，树中的每一个节点的胜率将代表综合各种可能的局面下的平均表现。

图1为应用于非完备信息博弈的UCT－RAVE算法伪代码，与蒙特卡罗抽样技术的结合使得UCT－RAVE算法在非完备信息博弈树的搜索问题中可以有效的运行并发挥自己的优势。

3 实例分析

为了验证本文方法在多人非完备信息博弈中的效果，选择了一个简单的三人争上游牌类博弈模型，争上游又称拱猪、跑得快等，游戏主要流行于江浙一带，游戏规则决定了玩家需要尽快把自己手中的牌尽量多的打出去，先把手中的牌出完的玩家获得胜利。失败的玩家，根据手中所剩的牌的数量计算，剩余的牌越多扣的分数越多，如图2所示。

图1 应用于非完备信息博弈的UCT－RAVE算法伪代码

图2 三人争上游牌类博弈画面

用不同的算法作为玩家出牌的策略进行游戏，比较不同算法的性能表现。为更好的做出比较，限制每次用两种算法控制3个玩家进行博弈，即只有两种类型的玩家，用Type A和Type B表示，同时为了消除位置对算法胜率的影响，选择表1所示的6种不同的位置排列，并平均各种位置排列下算法的表现。

表1 两种类型玩家的不同位置排列

选取UCT－RAVE算法参数C值为0.44，k值为100，模拟次数取5000，分别与UCT算法、随机 （Random）策略方法进行比较，每种位置排列进行1000次博弈，取平均计算胜率和失败时剩余的牌的数量，结果如表2所示。

表2 UCT－RAVE算法对战结果

由表2可以看出，在上述参数设置情况下，本文算法对随机策略时胜率在95%以上，说明了本文算法适用于多人非完备信息博弈模型，表现出一定的智能，和随机的胡乱出牌有质的区别。对UCT算法的胜率在75%左右，说明了本文算法的智能水平。

为研究模拟次数对本文UCT－RAVE算法的智能影响，选取10至10000区间内的若干模拟次数，并与此模拟次数下的UCT算法进行博弈比较，结果如图3所示。

图3 不同模拟次数下UCT－RAVE算法的性能

图3 横坐标为两种算法所用的蒙特卡罗模拟次数，纵坐标为本文UCT－RAVE算法对UCT算法的胜率，图中曲线表示随着模拟次数变化UCT－RAVE对UCT算法的胜率的变化情况。

从图3中可以看出，本文UCT－RAVE算法对战UCT算法能够取得70%以上的胜率，而从模拟次数的角度分析，本文UCT－RAVE算法可以在比较少的模拟次数下取得较好表现。在模拟次数极少 （50次以下）的情况下本文UCT－RAVE算法的胜率在50%以下，原因在于过少的模拟次数不能较准确的积累强化学习的数据，使得到的RAVE值很不准确，从而干扰了UCT的选择。随着模拟次数的不断增加，胜率呈下降趋势，是因为大量的模拟次数足以获得准确的胜率值，对RAVE的依赖逐渐减少。

4 结束语

本文详细介绍了UCT－RAVE算法的原理和特性，提出了将其与蒙特卡罗抽样技术相结合应用于多人非完备信息博弈中，首先通过蒙特卡罗抽样技术将非完备信息转化为有一定可信度的完备信息，然后基于此完备信息运用UCTRAVE算法进行搜索，最后综合多次蒙特卡罗抽样下的最佳平均收益，选择最适行动。通过简单的三人争上游牌类博弈实验证明此方法可行有效，并且同样模拟次数下能够获得比UCT算法更好的性能表现。但是如何选择本文UCT－RAVE算法的参数以获得更好的性能表现有待进一步研究。

［1］Sturtevant N R，Bowling M H.Robust game play against unknown opponents ［C］.Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems.USA：ACM，2006：713－719.

［2］Sturtevant N R.An analysis of UCT in multi－player games［C］.Proceedings of the 6th International Conference on Computers and Games.Berlin：Springer，2008：37－49.

［3］Chaslot G，Saito J T，Bouzy B，et al.Monte－Carlo strategies for computer go［C］.Proceedings of the 18th BeNeLux Conference on Artificial Intelligence.Park：AAAI Press，2006：83－91.

［4］Coulom R.Efficient selectivity and backup operators in Monte－Carlo tree search ［C］.Proceedings of the 5th International Conference on Computers and Games.Berlin：Springer，2006：72－83.

［5］Krauth W.Algorithms and computations［M］.England：Oxford University Press，2006：264－275.

［6］Sylvian Gelly，WANG Yizao，Remi Munos，et al.Modification of UCT with patterns in Monte－Carlo go ［R］.France：INRIA，2006：221－224.

［7］Kocsis L，Szepesvari C.Bandit based Monte－Carlo planning［C］.Proceedings of the 17th European Conference on Machine Learning.Berlin：Springer，2006.

［8］Gelly S，WANG Yizao.Exploration exploitation in Go：UCT for Monte－Carlo go ［C］.Twentieth Annual Conference on Neural Information Processing Systems.Canada：Citeseer，2006：225－236.

［9］WANG Y，Gelly S.Modifications of UCT and sequence－like simulations for Monte－Carlo go ［C］.IEEE Symposium on Computational Intelligence and Games.USA：IEEE，2007：175－182.

［10］Winand M H M，Bjornsson S Y，Saito J T.monte－carlo tree search solver［C］.Proceedings of the 6th International Conference on Computers and Games.Berlin：Springer，2008：25－36.

［11］Gelly S，Silver D.Combining online and offline knowledge in UCT ［C］.Proceedings of the 24th International Conference on Machine Learning.USA：ACM，2007：273－280.

［12］Silver D，Sutton R，Muller M.Reinforcement learning of local shape in the game of go ［C］.Proceedings of the 20th International Joint Conference on Artifical Intelligence.India：Hyderabad，2007：1053－1058.

［13］Nathan Sturtevant，Adam White.Feature construction for reinforcement learning in hearts［C］.Proceedings of the 5th International Conference on Computers and Games.Berlin：Springer，2006：1305－1310.

［14］Buro M，LONG J R，Furtak T，et al.improving state evaluation，inference，and search in trick－based card games ［C］.Proceedings of the 21st International Jont Conference on Artifical Intelligence.USA：ACM，2009：1407－1413.

［15］Arpad Rimmel，Fabien Teytaud，Olivier Teytaud.Biasing Monte－Carlo simulations through RAVE values ［C］.The International Conference on Computers and Games.Berlin：Springer，2010：59－68.