基于哈达玛变换的多元时间序列聚类研究

韩 娜，滕少华，房小兆

（广东工业大学 计算机学院，广东 广州510006）

0 引 言

时间序列分析是数理统计这一学科中应用性较强的一个分支，在金融经济、气象天文、信号处理、机械振动等众多领域有着广泛的应用［1］。聚类问题是时间序列模式发现的一个重要问题［2］。目前大部分研究主要针对一元时间序列的降维和相似性度量方法，多元时间序列聚类的研究还很少见。但是，现实世界中反映某一客观事物仅靠一个参数是不够的，大多数事物需要多个参数进行度量，如股票一般具有开盘价、收盘价、最高价、最低价等，多元时间序列是普遍存在的。当前对多元时间序列聚类方面的研究及存在的问题如下：Huang等采用主成分分析 （principal component analysis，PCA）方法聚类多变量时间序列［3］。这种方法当整个数据集的方差无法事先确定时有很大的局限性，而且在特定情况下，各对象确定的主成分数量不能一致，必须经过统一协调才能进行主成分分析且其不适合小规模数据集；Wang和McGreavy将每个多变量时间序列表示成m×n矩阵，然后将矩阵的每个元素展开成行向量来进行聚类［4］。这种方法只能聚类具有相同参数个数和序列长度的多元时间序列且计算复杂度会随着序列维数的增多而剧增；Kiyoung Yang［5］把多元时间序列看成矩阵，应用矩阵的Frobenius范数［6］度量多元时间序列的相似性，但它直接对原始时间序列进行处理，对于大规模数据集时间开销较大。文献 ［7－9］中利用傅立叶变换进行时间序列数据降维。傅立叶变换使我们可以从信号的时域和频域两个角度观察和分析信号，但是二者却是绝对分离的。对于傅立叶频谱中的某一频率，不知道这一频率是何时产生的，只能从全局上分析信号。这样在信号分析中就面临一对最基本的矛盾：时域和频域的局部化矛盾。

针对多元时间序列不等长、数据量大及参数间的相关性等特点，文中提出基于离散哈达玛变换及带权值的矩阵相似性度量的多元时间序列聚类方法并进行了实验验证。

1 离散哈达玛变换的维归约

1.1 离散哈达玛变换

离散哈达玛变换 （Descrete Hadamard Transform（DHT）h）的本质是将离散序列x（n）的各项值的符号按一定规律改变后，进行加减运算，它是一种线性运算，比采用复数运算的离散傅立叶变换 （DFT）和采用余弦运算的离散余弦变换 （DCT）计算相对简单。

定义1 一个长度为N的离散时间序列x（n），且N＝2q（q为正整数），哈达玛变换［10］为

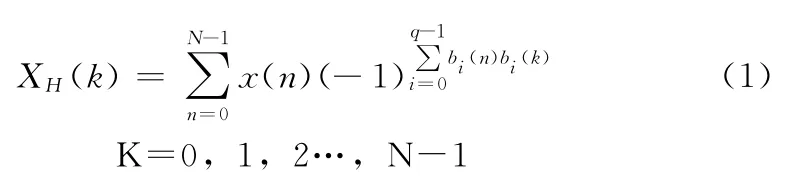
式中：bi（x）——非负整数的二进制形式的第i位，例如6的二进制表示为110，则b0（6）＝0；b1（6）＝1；b2（6）＝1。

哈达玛变换用哈达码矩阵表示更直观，且简单易懂。哈达玛矩阵是由＋1和－1构成的正交矩阵，实数表示且计算简单，用其进行序列变换具有高效的数据能量集中性。

定义2 一个长度为N的离散时间序列x（n）＝［x（0），x （1），x （2），…，x （N－1）］，其哈达玛变换表示为：XH（K）＝ ［XH（0），XH（1），XH（2），…，XH（N－1）］；哈达玛矩阵为

则哈达玛变换的矩阵表示为

定理1 设XH（K）是序列x（n）经离散哈达玛变换后的序列，则序列变换前后保持能量不变，即

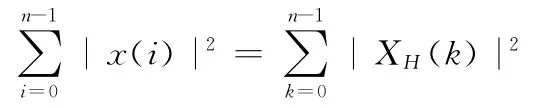
证明：离散哈达玛变换是正交变换，正交变换在欧氏空间中保持内积，得证。

1.2 数据降维

多元时间序列数据进行离散哈达玛变换，是在对多元时间序列数据进行能量集中的情况下，抽取多元时间序列前K个系数作为特征维，将不等长多元时间序列映射到K维特征空间，降不等长的多元时间序列转换成长度为K的多元时间序列。首先应对原始多元时间序列数据进行预处理，为了解决基线和刻度问题，最好的方法是使用序列数据规范化变换［11］。对多元时间序列的每一元时间序列利用公式进行规范化变换，其中，μ为原时间序列x的平均值，σ为原时间序列x的标准差，X为规范化变换后的序列。

对预处理后的多元时间序列数据进行维归约的方法如下：

（1）用二进制反码的格雷码建立按哈达玛编号的离散沃尔什－哈达玛变换后序列和按沃尔什编号的离散沃尔什－哈达玛变换后序列的映射关系。

（2）对x进行离散哈达玛变换。变换后的序列为XH。

（3）利用 （1）对XH进行调序，得到X。X即是我们需要的 （DWHT）H变换后的序列。

多元时间序列经过哈达玛变换后，取前K维，则不等长的多元时间序列都映射到K维的特征空间。由定理1可知，变换后的长度为K的多元序列能很好的保持原多元时间序列数据的趋势特征，这是实现多元时间序列快速有效聚类的必要前提。

2 带权值的矩阵相似性度量

2.1 多元时间序列权值的获取

多元时间序列并不是简单的一元时间序列的组合，通常多元时间序列的多个参数之间存在一定的关联，这些参数应该作为一个整体看待而不应该割裂开来［12］。为了更好的进行多元时间序列的相似性度量，这里考虑多元时间序列各个参数之间的相关系数。

多元时间序列A （M×N）经过离散哈达玛变换进行能量集中后，抽取前K个系数作为特征维，得到矩阵A（K×N）表示原多元时间序列，其能很好的保持原多元时间序列数据的趋势特征。首先，求变换后矩阵A （K×N）的相关系数矩阵A （N×N），然后，求相关系数方阵的特征根σA＝ ［σA1，σA2，…，σAN］，最后，σA与矩阵 A （K×N）的各列向量一一对应，作为矩阵相似性度量的权值。

2.2 带权值的矩阵相似性度量方法

目前，一元时间序列的相似性度量一般是基于距离，但这种方法显然已经不再适合多元时间序列的相似性度量。多元时间序列数据的相似性度量大都致力于其形态特征变换趋势的相似性，比如，对于股票，人们更关注的是股票价格序列的涨跌情况，而不是股票的具体价格。多元时间序列基于带权值的矩阵相似性度量，文献 ［13］中的相似性度量公式，能很好的表现多元时间序列数据的形态特征变换趋势。

两个不等长的多元时间序列A （M×N）和B（Q×N），利用离散哈达玛变换数据能量集中并进行K维归约后，能保持原多元时间序列数据的变换趋势特征且长度相同，其相应的变换后矩阵为

式中：K——矩阵A和B的行，即多元时间序列维归约后的序列长度，N——两多元时间序列的参数个数。σ＝［σA1，σA2，…，σAN］和τ＝ ［τB1，τB2，…，τBN］分别为矩阵A和B各列相对应的权值。则带权值的矩阵相似性度量定义如下

式中：wi——新的权值，表示如下

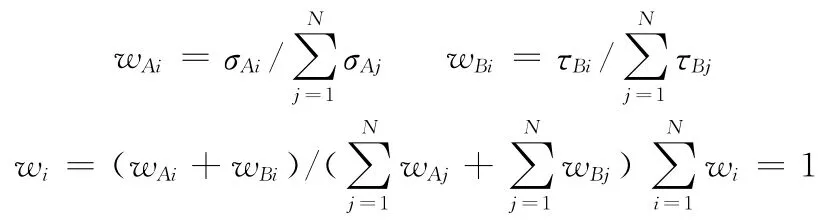
式中：｜＜ai，bi＞｜——矩阵A和B内积的绝对值。当sim （A，B）的值越大时表示矩阵A和B越相似，即表示多元时间序列A （M×N）和B（Q×N）的趋势形态特征变化越一致。

3 改进的K－means聚类算法

提出的基于哈达玛变换和带权值矩阵相似的聚类方法，首先用离散哈达玛变换对多元数据进行降维。然后求出多元变量相关系数矩阵的特征值作为权值。最后采用带权值的矩阵相似性度量方法，利用改进的K－means算法对多元时间序列进行聚类分析。

（1）K－means聚类是目前应用最为广泛的聚类算法之一。K均值聚类算法的具体步骤如下：1.初始化k个聚类中心c1，c2，…ck（可随机选取k个观测点作为聚类中心）；2.循环执行如下操作步骤：①将数据集中的观测点根据它与聚类中心相似度的大小，把它分配到距离最近的类；②重新计算聚类中心，重复步骤2直到将聚类中心不再发生变换或者聚类次数达到了算法设定的最大循环次数。

根据以上对K－means算法的分析，它具有算法简单且收敛速度快的特点［15］，该算法也适合于研究多元时间序列的聚类分析。

为了更好地实现不等长多元时间序列聚类，在数据预处理的前提下，对K－means算法进行如下改进：

（2）利用层次聚类算法，采用式 （3），找到K个变换后的矩阵及其相应的权值向量作为聚类中心；

（3）将D中所有的元素 （D为n个变换后矩阵的集合），根据相似性大小，分配到相似性最大的簇中；

（4）重复计算每个新簇的中心 （每个簇中各个变换后矩阵的平均值及权值向量的平均值）；

（5）重复 （2）、 （3）直至簇中心不再发生变化或迭代次数超过设定的最大迭代次数。

改进算法的时间复杂性为o（knd），其中n为多元时间序列个数，K为聚类个数，d为多元序列参数个数，K与d远远小于n。

4 数据实验验证

本文选取2009年30支长度为239的股票数据，均取自sohu网的财经板块16。它们有开盘价、最高价、收盘价、最低价4个参数，具体如下：1包钢稀土、2宝钢股份、3波导股份、4东风汽车、5歌华有线、6哈飞股份、7航天机电、8华夏银行、9建发银行、10金地集团、11马钢股份、12民生银行、13上港集团、14上海能源、15四川长虹、16铁龙物流、17铜陵有色、18维科精华、19武汉控股、20新疆城建、21郑州煤电、22中国船舶、23中国石化、24中国石油、25中国银行、26中青旅、27中信证劵、28中原高速、29重庆啤酒、30紫金矿业。对以上股票数据进行聚类分析，30支股票分为4类。

经查文献了解，目前国内对于多元时间序列的研究大多致力于相似性研究，对多元时间序列聚类的算法研究才刚刚起步。下面用实验来验证本文方法在实现多元时间序列高效降维的基础上，聚类的准确性也有所提高，本文采用两种实验方法。方法1：用哈达玛变换进行维归约，用式（3）的相似性度量进行聚类分析；方法2：用4层小波变换进行维归约，用式 （3）的相似性度量进行聚类分析。维归约后多元时间序列长度为K，聚类结果只给出股票代号。

由实验结果表1～表4观察可知，两种方法的聚类准确性都随着选取序列长度的增长而提高，但是，当选取的序列长度继续增长时聚类准确性会成降低趋势。实验结果表明多元时间序列利用离散哈达玛变化比离散小波变换具有更好的能量集中性即维归约性能。

表1 序列长度为4时的聚类结果

表2 序列长度为6时的聚类结果

表3 序列长度为8时的聚类结果

表4 序列长度为16时的聚类结果

由以上聚类结果及其趋势特征变换图分析，最终准确性高的聚类结果应如表3所示，两种方法中第一类和第三类中包含的股票代号相同。第二类和第四类包含的股票代号不同，主要差别是代号为12、16、19三支股票的归属。3种股票的立体三维趋势形态特征用matlab7.1中的surf（X，Y，Z）函数绘制而成，其中，3个参数坐标为X－维度（多元时间序列中参数的个数），Y－时间 （时间序列的时间间隔），Z－股票价格。股票趋势形态如图1所示，5、15号股票的趋势形态特征是第二类股票形态特征的代表，9号股票的趋势形态特征是第四类股票形态特征的代表。由图1可以看出12号股票和第四类股票形态相似，16、19号股票与第二类相似。由以上分析可知，序列长度取8时聚类效果较好，能有效地把不同趋势变化形态的股票分配到不同的类中，即同一类中的股票趋势形态特征尽可能的相似，不同类中的股票趋势形态特征尽可能的不相似。实验聚类结果说明文中带权值的相似性度量方法能很好的度量多元时间序列间的相似程度，同时，由图1可以看出方法1比方法2的聚类准确性要高，说明离散哈达玛变换方法比离散小波变换方法进行维归约，前者数据能量集中性要高于后者。实验结果证明，基于离散哈达玛变化进行维归约和带权值的矩阵相似性度量的方法，能有效的实现多元时间序列有效聚类分析。

5 结束语

多元时间序列聚类的研究仍处于发展中，利用单元时间序列哈达玛变换降维方法，其数据能量集中性相对较高。基于加权矩阵相似性原理，本文提出了基于哈达玛变换的多元时间序列聚类研究方法。实验结果表明，该方法能够很好的实现多元时间序列聚类分析，把具有相同趋势变化的多元时间序列分配到同一类中.当然，多元时间序列权值的选择不同对结果有一定的影响，在以后的研究中，还需考虑如何更科学的考虑权值的确定问题。

图1 股票的形态特征变换趋势

［1］WANG Qin.Time series analysis and application ［M］.Chengdu：Southwest Jiaotong University Press，2008 （in Chinese）. ［王沁.时间序列分析及其应用 ［M］.成都：西南交通大学出版社，2008.］

［2］LAST M，Klein Y，Kandel A.Knowledge discovery in time series databases ［J］.IEEE Trans on Systems，Man and Cybernetics，2001，31 （1）：160－169.

［3］HUANGY，McAvoy T J，Gertler J.Fault isolation in nonlinear systems with structured partial principal component analysis and clustering analysis［J］.Can J Chem Engr，2000，78 （2）：569－577.

［4］WANG X Z，McGreavy C.Automatic clalssification for mining process operational data ［J］.Eng Chem Res，1998，37 （6）：2215－2222.

［5］YANG Kiyoung，Cyrus Shahabi.A PCA based similary multivariate time series［J］.IEEE Transactions on Knowledge and Data Engineering，2005，17 （9）：65－74.

［6］ZHANG Xianda.Matrix analysis and application ［M］.Beijing：Tsinghua University Press，2004 （in Chinese）.［张贤达.矩阵分析与应用 ［M］.北京：清华大学出版社，2004.］

［7］Moon Y S，Kim J.Efficient moving average transform－based subsequence matching algorithms intime－series database ［J］.Information Sciences an Inter－National Journal，2007，177（23）：5415－5431.

［8］Kim S W，Park D H，Lee H G.Efficient processing of Subsequenee matching with the Euclidean metric in time－series databases［J］.Information Processing Letters，2004，90 （5）：253－260.

［9］Kontaki M，Papadopoulos A N， Manolopoulos Y.Adaptive similarity search in streaming time series with sliding Windows ［J］.Data ＆Knowledge Engineering，2007，63 （2）：478－502.

［10］QIAO Zhiwei，WEI Xueye，HAN Yan.Implement high speed linear convolution using fast Hadamard transform ［J］.Journal of Electronic Measurement and Instrument，2010，24 （3）：263－267（in Chinese）. ［乔志伟，魏学业，韩焱.用快速哈达玛变换（FHT）实现高速线性卷积 ［J］.电子测量与仪器学报，2010，24 （3）：263－267.］

［11］HAN Jiawei.Data mining：Concept and technology ［M］.2nd ed.Beijing：Mechanical Industy Press，2006 （in Chinese）. ［HAN Jiawei.数据挖掘：概念与技术 （英文版）［M］.2版.北京：机械工业出版社，2006.］

［12］YANG K，Shahabi C.A PCA－based similarity measure for multivariate time series［C］.Proceedings of the 2nd ACM International Workshop on Multimedia Databases.Washington，DC，USA：ACM Press，2004.

［13］MAO Hongbao，ZHANG Fengming.Similarity query in multivariate time series based on parameter importance degree［J］.Computer Engineering，2009，35 （24）：54－56 （in Chinese）.［毛红保，张凤鸣.基于参数重要度的多元时间序列相似性查询 ［J］.计算机工程，2009，35 （24）：54－56.］

［14］ZHANG Jianpei，YANG Yue，YANG Jing，et al.Algorithm for initialization of K－means clustering center based on optimized－division［J］.Journal of System Simulation，2009，21（9）：2586－2590.

［15］Ordonez C，Omiecinski E.Efficient disk based K－means clustering for relational databases［J］.IEEE Trans on Knowledge and Data Engineering，2004，16 （8）：909－921.

［16］http：//business.sohu.com/ ［OL］.