查找表联合记忆效应补偿技术的宽带自适应预失真算法

胡 欣 王 刚 王自成 罗积润

①(中国科学院电子学研究所中国科学院高功率微波源与技术重点实验室 北京 100190)

②(中国科学院电子学研究所中国科学院空间行波管研发中心 北京 100190)

③(中国科学院研究生院 北京 100039)

1 引言

随着通信技术发展，频谱资源日趋紧张, 频谱利用率较高的调制方式(如M-QAM)和传输技术(如OFDM, WCDMA)得到了广泛应用，而这类传输信号具有较高峰均值比，对大功率放大器的线性度提出了更高要求。目前大功率放大器通常在饱和状态下，可以保证较高的功率输出，但此时线性特性较差，且在宽带系统中表现有记忆效应[1-3]。大功率放大器记忆效应的非线性对通信信号的影响主要表现在两个方面：一是信号星座发生变形，造成码间干扰；二是频谱再生，造成邻近信道间干扰。码间干扰会增加通信系统的误码率，邻信道间干扰会影响邻近信道信号的正常传输和质量。目前解决大功率放大器的非线性影响主要是在发射端采用线性化技术，线性化技术可以保证功率资源和频谱资源的有效利用，同时保持传输信号的良好谱分布，且不会对邻近信道造成干扰。

通常预失真方法大多是针对无记忆的功率放大器提出的。随着移动通信业务的发展，带宽的增加使功率放大器的记忆效应不可忽略，无记忆预失真方法已经不能满足宽带和多载波发射机的线性化需求。因此文献[4]改进了无记忆预失真技术，提出了基于记忆多项式的预失真器，可以有效地校正记忆型功率放大器的非线性和记忆效应。不过，此类预失真器对多项式项数要求较高，且随着记忆深度的增加，其项数数量迅速增长，计算复杂度大，不易实现。为了降低计算复杂度，文献[5]提出了2维查找表记忆型预失真器，其计算复杂度较小，但短时功率统计量对记忆性的表征比较模糊，对记忆型功率放大器的线性化效果不如记忆多项式；同时，随着功率放大器记忆性变强，线性化效果会变得更差，且查找表的表格数量过小会引入量化失真，加大查找表的表格数量又会导致收敛速度变慢[6]。以上预失真器各有优缺点，但都面临同一个问题，就是记忆效应不能精确地评估，因此如何选择合适的参数去克服记忆效应会遇到一定困难。本文将记忆多项式[4]和查找表[7]联合使用，介绍一种可以有效克服功率放大器非线性和记忆效应的预失真技术。本文利用查找表的方法通过分析功率放大器输出信号频谱特性能够对功率放大器的记忆效应进行评价和鉴定，以便合理选择相应参数克服记忆效应来降低整个预失真算法计算复杂度。在此基础上，利用内插值方法有效减小了幅度量化产生的误差，从而保证较少的查找表表格数量，也在一定程度上降低了查找表更新过程的计算复杂度。利用内插方法处理的查找表与多项式技术相结合，在得到较好线性化效果的同时还能最大程度减小计算复杂度。最后通过仿真验证了本文预失真器对记忆型功率放大器的良好线性化效果。

2 基于查找表的基带预失真器方案设计

多项式与查找表技术[7]相结合就是在无记忆查找表技术的基础上增加记忆效应补偿器，其具体实现框图如图1所示。第1个虚框中主要是记忆效应补偿器，由M个分支并联组成，每个分支由一个非线性函数Fm(·)和一个传输函数Hm(·)组成，具体的实现形式如式(1)所示[6]：

第2个虚框中是无记忆查找表结构，功率放大器的输入信号x(n)经过耦合器三等分后，在主路、支路1和支路2上的信号分别为x1(n),x2(n)和x3(n)。在支路2中，由于支路2中的信号与主路上信号相等，利用|x3(n)|来代表当前信号的幅值，以其作为索引，选择主路中当前信号x1(n)对应的表项值F。同时在主路上，输入信号x1(n)与被索引的对应表项值F相乘得到预失真信号u(n)，其通过增益G(u)的功率放大器后输出信号为y1(n)。在支路1中，经过一定时延D的输入信号x2(n)和经过处理的功率放大器输出信号y2(n) =y1(n) /GPD(0＜GPD≤G,G为功率放大器的小信号增益)作为自适应模块的两个输入信号，这里的自适应模块可以利用文献[7]中自适应算法实现查找表表项更新。其中查找表各表项之间是相互独立的，每次迭代只能对一个表项进行更新。因此，表项越少，收敛越快，但量化误差也越大。在工作过程中，量化误差类似于噪声，影响了线性化效果的提高。查找表的尺寸越大，表项越多，量化误差越小，但收敛速度也越慢，对系统存储量的要求也越高。

待查找表更新完毕后，再利用自适应模块中的递归最小二乘(RLS)算法[8]更新记忆效应补偿器中的多项式系数。这种更新方式的好处是可以根据查找表预失真器的实际线性化效果来灵活选择合适的多项式项数，尤其是确定大致的记忆深度，以便保持尽量小的计算复杂度。

图1 基于查找表的记忆型预失真器

针对查找表本身存在的量化失真问题，采用内插值方法[9]有效减小了幅度量化产生的误差。在查找表的量化失真得到补偿后，可以一定程度上减小查找表表项数量，避免查找表的量化噪声影响到整个预失真器对功率放大器的线性化效果。常用内插方法有线性内插和拉格朗日多项式内插，线性内插实现简单，易于实时计算。线性内插值[9]如式(2)所示，其中当前输入信号幅度|x|处于查找表的(|x1|,|x2|)幅度范围内。

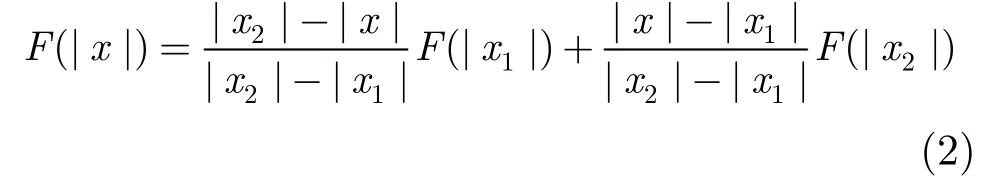
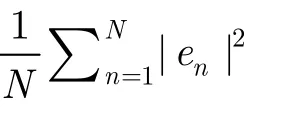
表1 无内插和线性内插查找表方案

主路上实现记忆效应补偿的多项式系数更新采用间接学习结构，此时自适应模块中的辨识网络和主路上的记忆效应补偿器具有完全相同的结构和参数，这里辨识网络可以用式(1)的多项式结构表示。与文献[4]中记忆多项式预失真器不同之处在于，多项式的最高阶数K一般选为3即可，大大降低了多项式项数。为了得到式(1)中合适的系数，自适应模块采用递归最小二乘法(RLS)算法[8]。算法具体流程如图2所示，当给定初始条件后，预失真器开始工作在无记忆查找表预失真状态，并判断此刻的无记忆预失真效果是否满足预期初步线性化指标。若满足初步预期线性化指标，则开始工作在记忆效应补偿状态，否则利用文献[7]中的自适应算法继续更新查找表。当工作在记忆效应补偿状态后，通过计算一定数量输入输出信号的均方误差值来判断是否需要继续进行记忆效应补偿，若不满足均方误差的要求则利用RLS算法计算并继续更新主路记忆效应补偿器。否则，判断此时的预失真器是否校正记忆效应和非线性失真，若满足要求则结束自适应操作，否则，返回重新进行自适应预失真。

图2 本文预失真方法流程图

3 算法仿真及性能分析

本文主要验证预失真算法对宽带信号的有效性，这里选择OFDM宽带信号作为功率放大器的信号源。预失真系统的 OFDM 信号仿真过程如图 3所示，为简单起见，图中只列出了仿真过程的主要步骤。信号源产生的随机整数经过4QAM调制，然后通过串并变换分成 1705个数据流，再进行4096点的 IFFT变换得到一帧数据，最后经过并串转换得到OFDM的基带信号。信号经滤波器处理后，进入预失真器形成预失真信号，再送入功率放大器。预失真系统采用本文图3所示结构，并运用本文预失真算法更新预失真器参数。信道模型采用加性高斯白噪声信道(AWGN)模型。在接收端，利用快速傅氏变换和 4QAM 解调恢复原始信号。本文中将OFDM 符号的持续时间TS定为 280 μs,TS由有用部分的持续时间TU和保护间隔持续时间D组成，分别为224 μs和56 μs，对应的OFDM信号频谱带宽为7.61 MHz。

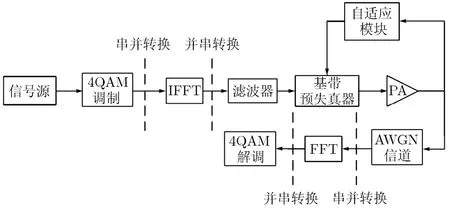
图3 OFDM基带预失真系统仿真流程图

在仿真中，非线性功率放大器选用式(3)所示的记忆多项式模型，

其中K是预失真器和功率放大器多项式模型的最高阶数，M是记忆长度，akm是功率放大器多项式模型系数，分别如下：

仿真过程中的其它设置条件如下：过采样因子为4，整形滤波器采用滚降因子为0.22的升余弦滤波器，预失真器的阶数为3，记忆长度为5。

图4为未编码的4QAM-OFDM信号通过非线性功率放大器后的误比特率性能仿真曲线，无预失真时由于功率放大器的非线性失真误比特率严重恶化，与理想线性功率放大器差别较大。在误比特率0.002时，与理想线性功率放大器相比无预失真系统信噪比损失了4 dB左右。采用预失真技术后，误比特率可以得到一定程度改善。本文预失真与记忆多项式预失真技术对误比特率能有较大改善，接近理想线性功率放大器。而2维查找表预失真技术虽也有改善，但是改善效果不如本文预失真与记忆多项式预失真技术。

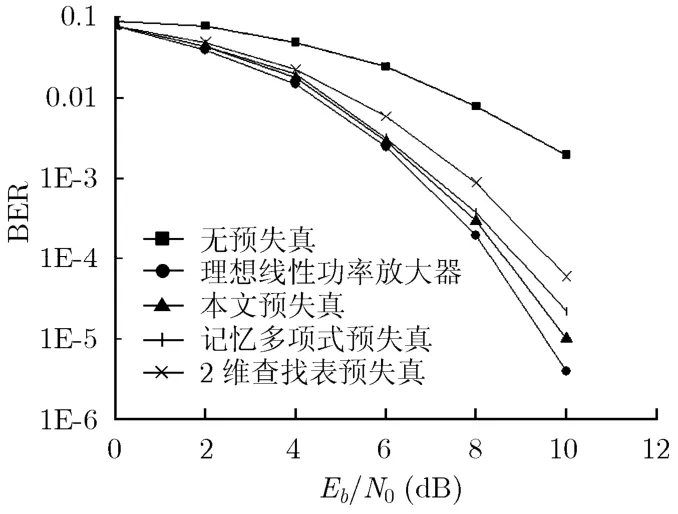
图4 误比特率性能曲线比较

在描述多载波系统或数字调制系统的功放时，不同频率之间相互调制的情况是非常复杂的，用简单的双音分析远远不够准确，因此工程上采用邻道功率与主信道功率的比值ACLR(Adjacent Channel Leakage Ratio)分析功率放大器非线性特性，ACLR是AM/AM失真和AM/PM失真共同作用的结果。对于非恒定包络调制技术的现代无线通信系统，输入信号包络为非等幅的，在功放的过饱和区，由于非线性作用，输出信号的信号带宽会展宽，其频宽一般会高于恒定包络调制信号，这就会对其邻近信道产生交互调干扰，这种干扰会在一定程度上增加邻近信道的误码率。通过预失真技术可以改善ACLR的指标，ACLR越小则在一定的带宽内信道间的相互干扰就越小，误码率越小，频带利用率越高。通过分析功率放大器输出信号的功率谱特性来比较2维查找表预失真器[5](3张查找表，查找表表格数量均为256)、式(1)所示的记忆多项式预失真器[4](K=7和M=5)和本文预失真器(式(1)所示的记忆多项式模型，K=3,M=5和内插处理的表格数量为64的查找表)的线性化效果，结果如图5所示。

图5 OFDM宽带信号功率谱密度

对功率放大器输出信号的功率谱进行归一化处理，曲线(a)代表不采用线性化技术的功率放大器输出信号功率谱曲线，曲线(b)代表无记忆查找表预失真器的功率放大器输出信号功率谱曲线，曲线(c)代表2维查找表预失真器的功率放大器输出信号功率谱曲线，曲线(d)代表记忆多项式预失真器的功率放大器输出信号功率谱曲线，曲线(e)代表本文预失真器处理的功率放大器输出信号功率谱曲线，曲线(f)是功率放大器理想输出信号的功率谱曲线。在偏离载波中心频率 5 MHz处，如果不使用任何线性化技术，如曲线(a)所示，功率放大器ACLR指标大约-25 dBc；采用无记忆预失真器后，曲线(b)较曲线(a)的功率放大器ACLR指标被改善约10 dB。采用2维查找表记忆型预失真器的功率放大器ACLR指标被改善到了约-40 dBc，如曲线(c)所示。采用记忆多项式预失真器和本文预失真器的功率放大器ACLR指标得到了更大改善，达到约-45 dBc，且从平均的角度本文预失真器的效果略微好于记忆多项式预失真器，如曲线(d)和曲线(e)所示。如果采用不考虑记忆效应的预失真器，在窄带应用中可以取得良好线性化效果，但在宽带通信系统中，由于不能对功率放大器的记忆效应进行补偿，只能在一定程度上抑制带外频谱扩展，而考虑记忆效应的预失真技术，则可以更加有效抑制带外频谱扩展。记忆多项式及本文的预失真补偿效果和理想功率放大器ACLR指标较接近，但是仍有差别主要是因为输入信号为非恒包络信号，幅度较小的输入信号更容易受历史信号的影响，表现出较强的记忆效应，经预失真器补偿后，小信号区仍有部分记忆失真。

文献[5]中2维查找表预失真的自适应迭代更新过程的计算复杂度较小，但是预失真效果不如文献[4]中记忆多项式预失真器以及本文中的预失真器。为了获得较好的线性化效果，暂不考虑2维查找表预失真方法，表2列出文献[4]和本文两种预失真方法中自适应算法的计算复杂度，为了得到图6的线性化效果，文献[4]的记忆型预失真器需要通过RLS算法更新35个多项式系数，而本文预失真器在查找表更新完毕后仅需要更新15个多项式系数。也就是说完成一次迭代过程，文献[4]需要进行1995次乘法以及1925次加法或减法，而本文预失真器乘法和加法次数大幅减少，分别为405次和375次。主要是因为文献[4]的记忆多项式型预失真器需要对功率放大器的非线性失真和记忆效应两方面进行补偿，会需要较多的多项式项数才能得到较好的线性化效果。而本文预失真器首先利用查找表对功率放大器的非线性失真进行补偿，多项式作用主要是用来补偿功率放大器的记忆效应，需相对少的多项式项数就可以得到较好的线性化效果。

图6 学习曲线比较

本文预失真技术与文献[4]预失真技术的学习曲线如图6所示，本文预失真技术学习曲线是利用查找表对功率放大器的非线性失真进行补偿后的学习曲线。与文献[4]预失真技术学习曲线相比，由于查找表的作用，在初始迭代时本文的最小均方误差较文献[4]已有约17 dB的改善。两种预失真方法都可以将最小均方误差减小到约37 dB，但是所需的迭代次数不同，本文预失真技术的收敛速度得到了明显的提高。

4 结论

针对无记忆预失真技术在宽带应用中效果不理想的问题，本文提出了一种记忆型预失真线性化方法，用于校正宽带通信系统中功率放大器的非线性失真和记忆失真。当特定OFDM信号作为功率放大器的信号源时，在偏离载波中心频率 5 MHz处，采用2维查找表记忆型预失真器的功率放大器ACLR指标可以被改善到约-40 dBc，而分别采用记忆多项式预失真器和本文预失真器的功率放大器ACLR指标得到了更大改善，达到约-45 dBc，与理想功率放大器ACLR指标更为接近。记忆多项式预失真器和本文预失真器均能得到较好的线性化效果，但是与记忆多项式方法相比较，本文预失真方法计算复杂度大大降低。记忆型预失真器需要通过RLS算法更新35个多项式系数才能得到的线性化效果，本文预失真器仅需要更新15个多项式系数就可以实现。也就是说完成一次迭代过程，记忆多项式需要进行1995次乘法以及1925次加法或减法，而本文预失真器乘法和加法次数大幅减少，分别为405次和375次。随着通信技术发展，功率放大器线性化技术将会更多地用于宽带通信系统中，作为目前主流线性化技术之一的基带预失真技术必须适应这种变化，才能获得更广泛的应用。

表2 两种预失真方法的计算复杂度

[1]Muta O, Kaneko I, Akaiwa Y,et al.. Adaptive predistortion linearization based on orthogonal polynomial expansion for nonlinear power amplipers. Communications and Signal Processing (ICCSP), 2011 International Conference on Communications and Signal Processing (ICCSP), Kerala,India, Feb. 10-12, 2011: 512-516.

[2]Li Ji-xia and You Bin. Digital predistortion for power amplifiers with memory effects. Microwave Conference Proceedings (CJMW), China-Japan Joint, Hangzhou, China,April 2011: 1-3.

[3]Mkadem F and Boumaiza S. Physically inspired neural network model for RF power amplifier behavioral modeling and digital predistortion.IEEE Transactions on Microwave Theory and Techniques, 2011, 59(4): 913-923.

[4]Ding L, Zhou G T, Morgan D R,et al.. A robust digital baseband predistorter constructed using memory polynomials.IEEE Transactions on Communications, 2004, 52(1):159-165.

[5]Jung W J, Kim W R, Kim K M,et al.. Digital predistorter using multiple lookup tables.Electronics Letters, 2003,39(19): 1386-1388.

[6]Kim Jangheon, Woo Young-yun, Moon Jung-hwan,et al.. A new wideband adaptive digital predistortion technique employing feedback linearization.IEEE Transactions on Microwave Theory and Techniques, 2008, 56(2): 385-392.

[7]Cavers J K. The effect of quadrature modulator and demodulator errors on adaptive digital predistorters for amplifier linearization.IEEE Transactions on Vehicular Technology, 1997, 46(2): 456-466.

[8]Paulo Sergio Ramires DINIZ. Adaptive Filtering: Algorithms and Practical Implementation. Second Edition. Kluwer Academic Publishers, Boston: America, 2002, Chapter 5.

[9]叶其孝, 沈永欢. 实用数学手册. 北京: 科学出版社, 2006:711.