一种改进的分布式最大权独立集算法
2012-07-25王向阳
王向阳 张 源
(东南大学移动通信国家重点实验室 南京 210096)
1 引言
文献中已提出了几种分布式MWIS算法[6,8]。这些算法都是基于启发式的贪婪原则的。在文献[9]中,提出了一种新型的分布式MWIS算法。该算法直接应用了机器学习以及信道编码领域的信用传播(belief propagation)及最大乘(max-product)方法[10],使相邻节点之间不断交换包含软信息的消息,并且每个节点根据所有收到消息各自独立判断是否属于最大权独立集。如果图是树结构(即不含圈)的,该算法一定可以收敛至最优;如果图是一般结构(即含圈)的,则该算法被证明只有当对应的松弛的线性规划的最优解非分数时才可以收敛至最优。值得注意的是,该结论对图匹配问题来说一般也是成立的[11,12]。对于该分布式MWIS算法来说,可以通过修改其中的消息计算公式进一步提高性能。事实上,在文献[9]中已经提出了一种改进算法。该算法利用松弛原始线性规划的对偶规划,首先收敛至对偶问题的最优解,然后启发式地映射为原问题的解。这种基于对偶的改进算法被证明只有当图是二分图时,才能收敛至最优,仍然具有较大的局限性。
针对已有工作的不足,本文提出了一种新的改进的分布式MWIS算法。该算法以文献[9]中基于最大乘信用传播的分布式MWIS算法的迭代运行方式为框架,通过细致分析一般图中最大权独立集中元素构成的特点,启发式地提出一种新的改进的相邻节点间交换消息的计算公式以及节点判断的计算公式。这些计算公式将要求所有节点知道自己所有邻居节点之间是否有连接的信息。在该局部拓扑信息的帮助下,所提出算法可以摆脱文献中已有算法对图必须是树或者二分图的要求,在大多数情况下都可以收敛至最优解,具有更好的性能,并被仿真结果所验证。
本文接下来的部分组织如下。首先,第2节描述了一般图中的最大权独立集问题,并介绍了基于最大乘信用传播的分布式算法框架。第3节提出了一种新的相邻节点间交换消息计算的方法以及相应的分布式算法。第4节给出了新算法性能的仿真结果。最后,第5节对全文进行了小结。
2 最大权独立集问题
考虑一个一般的无向图G=(V,E),其中V代表所有节点的集合,E代表所有边的集合。如果任意两个节点i与j之间有一条边,即(i,j)∈E,则称这两个节点是相邻的。记N(i)为节点i的所有邻居节点构成的集合。每个节点i都被赋予一个正权重wi。任意V的一个子集都可以用变量集合x=(xi)来表示,其中xi=1表示节点i在该子集内,xi=0则表示节点i不在该子集内。在一个子集中,如果其中任意两个节点都不是邻居,在称该子集为独立子集(independent set)。本文研究如何寻找具有最大权重的独立子集,即最大权独立集(MWIS)。一般来说,MWIS问题可以表示为下列线性二值整数规划问题,
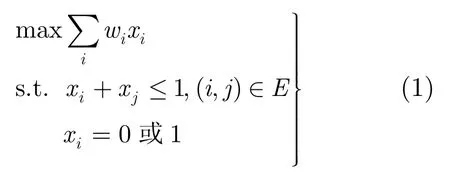
接下来,将简要介绍文献[9]中的基于最大乘信用传播的分布式MWIS算法。所谓信用传播,是一种来自人工智能与机器学习领域的非常基本的推断方法,并已在信道编解码领域获得非常成功的应用[10]。文献[9]将该方法直接应用于解决MWIS问题,得到了相应的分布式MWIS算法,选择其中包含两类消息的版本介绍如下。首先,该算法是以迭代方式运行的,其中在每次迭代过程中,每个节点i都要发送两类消息给自己的每个邻居节点j∈N(i),其计算公式为

接下来,每个节点i计算下列度量
传统静态地图主要用于描述和传递自然和人文地理环境特征,而信息时代下的地图已经不再局限于表达地理环境特征、实现科研用途等特定的领域,而是进入到了前所未有的全民位置地图新时代.以“互联网+”为代表的基于位置的服务无不都与地图相关,如实时路线导航、共享单车、外卖配送等,可以说地图的服务范围已经深入了到社会经济发展的各个部门.当前地图学教学和实践内容中仍主要以传统地形图教学为主,鲜有涉及地图服务的最新进展的系统化介绍,易造成学生所学知识用不到,用到的没学到等现象.因此,在教学内容改革中应补充和更新地图在不同领域最新应用的案例学习,做好课堂理论知识与实际应用出口的衔接,提高学生对地图的学习兴趣.

根据该度量,每个节点i进行如下判断:
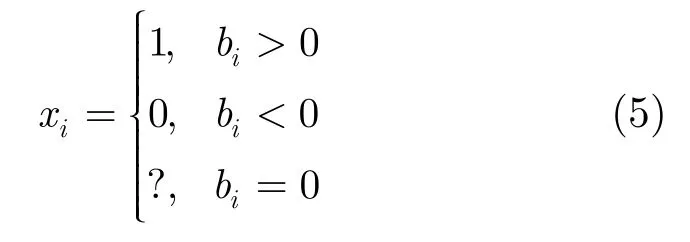
其中问号代表不确定情形。
在上述算法中,所有节点只与相邻节点交换消息,因此是分布式的。文献[9]证明了该算法只有当松弛线性规划的最优解非分数时才可以收敛至最优解。在该算法基础上,文献[9]提出了一种利用对偶的改进算法,并证明了只有当二分图时才能收敛至最优解,仍具有较大的局限性。
3 一种改进的分布式算法
上节中的式(2)-式(5)中的算法只适用于树结构,而在一般图中则无法保证其性能。对其中可能的原因启发式的定性分析如下。记U(x)=∑iwixi代表系统总效益函数(即总权重)。考虑某节点i,需要自己分别计算xi=1与xi=0时U(x)的最大取值,然后计算两者的差,称为净效益bi。如果净效益大于0,则可以取xi=1,否则就只能取xi=0。这就是bi与式(5)的物理含义。为计算bi,首先需要计算xi=1时U(x)的最大值。由于采用分布式算法,节点i只知道xi=1以及节点i的所有相邻节点k只能取xk=0,从而U(x)中至少包含wi项。至于其余节点的信息,节点i无法直接获得,只能通过接收邻居节点k的消息得到。记节点i的所有邻居节点组成集合为N(i)={i(1),i(2),…,i(|N(i)|)},其中|X|代表集合X中元素的个数。以每个节点i(n)为根,可以得到|N(i)|个子集Sn(i)(1≤n≤|N(i)|),其中i(n)∈Sn(i)。由于是树结构,任意两个子集Sj(i)与Sk(i)中的节点都不同且没有边相连,并且V= {i} ∪S1(i) ∪S2(i) ∪…∪S|N(i)|(i)。这样,节点i的每个邻居节点i(n)将负责计算当xi(n)=0时,子集Sn(i)中独立约束下总权重的最大值,然后报告给节点i使用。这就是消息qk→i的物理含义。这样,xi=1时U(x)的最大值就等于wi+∑k∈N(i)qk→i。 接下来还要计算xi=0 时U(x)的最大值。类似地,节点i只知道xi=0以及节点i的所有相邻节点k只能取xk=1。因此,每个节点i(n)将负责计算当xi(n)=1时,子集Sn(i)中独立约束下总权重的最大值,然后作为消息pk→i报告给节点i。这样,xi=0 时U(x)的最大值就等于∑k∈N(i)pk→i。综合这两方面的计算,可以得到bi的计算公式。这就是式(4)的物理含义。至此,关键问题在于如何计算消息。首先考虑qk→i。在计算qk→i时要考虑下列两方面的因素。一方面,由于xk=0,则qk→i中将不会出现wk项;另一方面,由于xk=0,则节点k的所有的相邻节点j则可以取xj=1。因此,qk→i应该等于所有相邻节点j发送给自己的消息pj→k的和,即式(3)所示的计算过程。接下来考虑pk→i。类似的,由于xk=1,则pk→i中将包含wk项;另一方面,由于xk=1,则节点k的所有的相邻节点j则只能取xj=0。因此,pk→i应该等于wk与所有相邻节点j发送给自己的消息qj→k的和,即式(2)中前一半所示的计算过程。在式(2)中的后一半计算过程则是基于下列简单的考虑,即如果将pk→i与qk→i合并为单个消息mk→i=pk→i-qk→i并且希望该消息是非负的,即mk→i≥0,那也就要求pk→i≥qk→i,即式(2)中后一半所示的计算过程。
上述是对式(2)-式(5)物理含义的分析,从中可以得到对算法进行改进的线索。事实上,上述分析表明,该算法主要基于下列推断:如果节点i的xi=1则节点i的所有相邻节点k都有xk=0,反之亦然,并以之为基础得到式(2)-式(4)中的计算公式。该断言在树结构下显然是正确的,但对一般图结构则一般是不成立的。这是导致该算法在一般图中无法保证性能的主要原因。为此,本文针对该导致性能下降的主要原因,提出了一种新的改进算法,以提高该类型算法在一般图中的性能。
在算法中包括有每节点度量的计算与节点间交换消息的计算两个部分,分别讨论如下。首先是每节点度量bi的计算。为计算bi,首先需要计算xi=1时U(x)的最大值。由于xi=1,则U(x)中至少包含wi项。接下来考虑节点i的所有相邻节点k。如果图是树,如图1(a)所示,则只能取xk=0;如果是一般图,由于寻找的是独立集,该性质仍然是成立的。因此,xi=1时U(x)的最大值就等于
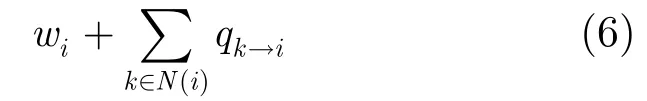
接下来要计算xi=0时U(x)的最大值。由于xi=0,则U(x)中将不会出现wi项。接下来考虑节点i的所有相邻节点k。如果图是树结构,如图1(a)中所示,则可以取xk=1;但如果是一般图,则要仔细分析各种可能的情况。事实上,考虑N(i)中的某两个节点l与n,如果这两个节点是相邻的,如图1(b)中所示,则这两个节点不可能同时xl=1与xn=1。因此,必须对N(i)中的所有节点进行分类。假设N(i)中包含有T(i)个独立子集Dt(i)(1≤t≤T(i)),如果xi=0,则只可能独立子集中的节点取xk=1。第t个子集Dt(i)中所有节点的权重为∑k∈D_t(i)pk→i。记具有最大权重的子集为D*(i),那么该子集中的节点都取xk=1,而非该子集中的节点都取xk=0。这样,xi=1时,U(x)的最大值就等于
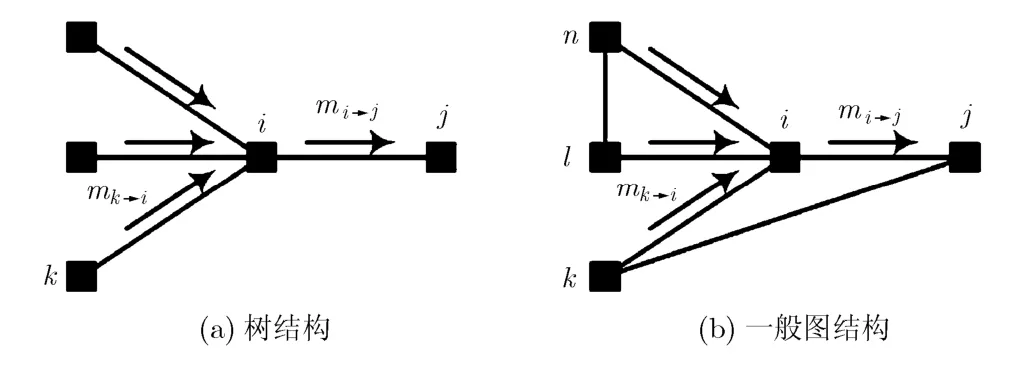
图1 树与一般图结构的对比

综合这两方面的计算,可以得到bi的计算公式为

接下来是节点间交换消息的计算。在节点间交换两类消息pk→i与qk→i,分别讨论如下。首先是消息qk→i。该消息所对应的情况为,由于xi=1,所以必然有xk=0,则节点k的相邻节点j∈N(k)有可能取xj=1。分情况讨论如下。首先,如果节点j与节点i有连接,如图1(b)中所示,则必然有xj=0。因此,需要将N(k)中所有与节点i相邻的节点剔除,还要把节点i也剔除,然后记剩下的节点构成的集合为N'(k)。接下来,对N'(k)进行类似于推导式(7)所做的处理。假设N'(k)中包含有T'(k)个独立子集(k) (1 ≤t≤T'(k)),其中D'*(k)是N'(k)的最大权重独立子集。这样,可以得到qk→i的计算公式为

接下来讨论消息pk→i。该消息所对应的情况为,由于xi=0,则在一般图中xk=0与xk=1都是有可能的。如果xk=0,则可以重复推导式(6)或式(9)的过程,可以得到pk→i的计算公式为
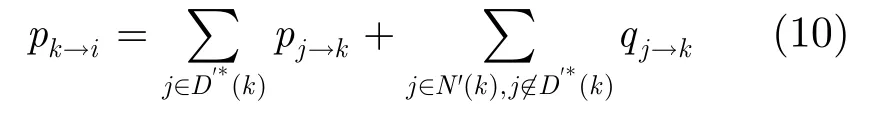
反之,如果xk=1,重复式(6)的推导过程,可以得到pk→i的计算公式为

综合这两方面的计算,可以得到pk→i的计算公式为
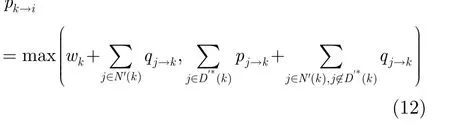
为简化起见,将pk→i与qk→i合并为单个消息mk→i=pk→i-qk→i。则式(8),式(9),式(12)中的计算公式可以简化为

综上,本文提出的分布式最大独立集算法的运行方式如下:
(1)初始化所有的消息mi→j=0;
(2)任意两个相邻节点k与i根据式(14)对消息mk→i进行更新;
(3)每个节点i根据式(13)计算信用度量bi的取值;
(4)每个节点i根据式(5)判断xi的取值;
(5)重复上述步骤2-步骤4直至收敛。
值得说明的是,在该算法中,需要每个节点计算D*(k)与D'*(k),这就需要每个节点能够了解自己邻居节点之间的连接情况,并寻找其中的最大权重子集。与传统算法相比,这增加了每个节点的通信复杂度与计算复杂度,分析如下。首先是通信复杂度。新算法要求每个节点获得邻居节点之间的局部拓扑信息。因此,每个节点要向自己的邻居节点广播自己的邻居节点列表,使得每个节点了解自己的邻居节点之间的连接情况。假设每个节点平均有n个邻居节点,为每个节点号编码需要B个比特,则任意两个相邻节点间在每个更新周期内将额外增加nB个比特的通信量。对于常见的无线网络来说(即非极端密集部署的),邻居节点数都较小,所带来的额外通信量一般来说不会很大。事实上,在一些已有系统标准(如IEEE 802.16)中,已经包含了这种广播邻居节点列表的操作了。第二是计算复杂度。新算法要求每个节点寻找自己与邻居节点组成的小网络中的最大权重子集。由于邻居节点仅限于单跳范围内,其规模一般来说是很小的,因此在其中寻找最大权重子集只需穷举即可。假设每个节点平均有n个邻居节点,则最大穷举次数平均不会超过2n,当n取值较小时,是比较容易实现的任务,所带来的额外计算量一般来说不会很大。综上,与传统算法相比,新算法增加了一定的通信与计算复杂度,但这样的复杂度是可以接受的。仿真试验表明,改进算法可以显著提高消息交换算法在一般结构图中寻找最大权独立集的能力,具体内容在下节中给出。
4 性能仿真
本节仿真验证新算法的性能。首先介绍仿真场景。假设在1 km×1 km的正方形区域内随机分布有若干节点。这样就可以得到一个图G=(V,E),其中V是所有节点组成的集合,且每个节点都随机产生一个0至1之间的数作为权重;E是所有边组成集合。其中如果任意两个节点之间距离小于某一门限值,则这两个节点间有边相连。在仿真中假设门限值为0.4 km。针对给定图,本文将分别运行3种不同的分布式MWIS算法。第1种算法就是文献中常见的基于贪婪的分布式MWIS算法,并选择了文献[8]中的算法作为例子。第2种算法就是文献[9]中的基于最大乘信用传播的分布式 MWIS算法,即式(2)-式(4)中给出的算法。第3种算法就是本文新提出的改进算法,即式(13)与式(14)中给出的算法。另外,我们还将通过最优化方法计算给定图中的最大权独立子集,作为分布式算法性能的上限。
主要考察两方面性能的比较,即算法输出独立子集的权重和性能的比较,以及算法寻找独立子集需要迭代次数的比较。分别假设节点总数为10, 20,30, 40, 50。在不同的节点总数下,随机生成100个不同的节点分布并得到相应的图,对每张图分别运行前述3种分布式MWIS算法以及穷举算法,然后把100次仿真的结果平均起来作为该节点总数下的仿真结果,分别画在图2和图3中。首先,从图2中示出了4类算法的平均性能,从中可以看出本文所提出的新算法几乎是最优的,其性能与最优化方法几乎是相同的;未经修改的基于信用传播的分布式算法[9]则明显性能较差,无法适用于一般图结构;而贪婪算法[8]则介于两类算法中的中间,其性能一般来说总是好于信用传播算法,但与本文的新算法则在性能上总是有一定的差距。接下来,在图3中示出了两类算法的平均迭代次数,从中可以看出本文所提出的新算法的迭代次数要多于信用传播算法,并且平均迭代次数随着节点数的增加而增加,而信用传播算法的迭代次数则较少且受节点数改变的影响不大。这主要是由于本文新算法相对比较复杂,从而需要较多的迭代次数,以换得了较好的性能。
5 结论
本文研究了一般图的最大权独立子集的分布式算法。以基于最大乘信用传播的分布式MWIS算法为框架,通过分析一般图中最大权独立集构成的特点,在所有节点了解自己邻居节点间局部拓扑信息的假设下,提出了一种改进的相邻节点间交换消息以及节点度量的计算公式,从而得到了一种新的改进算法。仿真结果表明,该新算法针对一般图进行设计,摆脱了文献中已有算法对图必须是树或者二分的束缚,能够达到近似最优的权重和性能。进一步的,本文算法的迭代次数多于信用传播算法,并且平均迭代次数随着节点数的增加而增加,而信用传播算法的迭代次数则较少且受节点数改变的影响不大。因此,本文算法是以较多的迭代次数换得了较好的性能。该算法的提出对于研究无线网络资源调配、无线骨干网构建等问题的一般方法具有一定的参考价值。

图2 平均独立子集权重和性能的比较
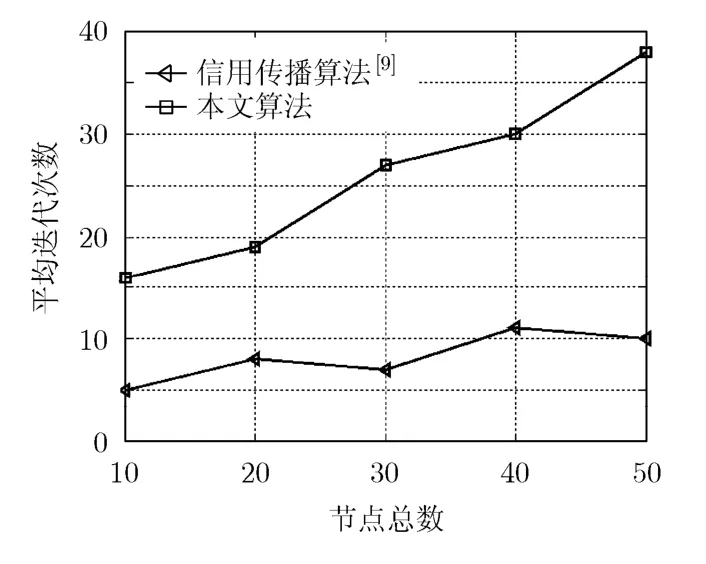
图3 寻找独立子集需要平均迭代次数的比较
[1]Dasgupta S, Papadimitriou C, and Vazirani U. Algorithms[M]. New York: McGraw-Hill, 2008, Chapter 8.
[2]Wang P and Bohacek S. Practical computation of optimal schedules in multihop wireless networks[J].IEEE/ACM Transactions on Networking, 2011, 19(2): 305-318.
[3]Lv S, Wang X, and Zhou X. Scheduling under SINR model in Ad hoc networks with successive interference cancellation[C].2010 IEEE Global Telecommunications Conference(GLOBECOM 2010), Miami, Florida, USA, Dec. 6-10, 2010:1-5.
[4]Li H, Cheng Y, Zhou C,et al.. Multi-dimensional conflict graph based computing for optimal capacity in MR-MC wireless networks[C]. 2010 IEEE 30th International Conference on Distributed Computing Systems (ICDCS 2010), Genova, Italy, June 21-25, 2010: 774-783.
[5]Li Y, Guo L, and Prasad S K. An energy-efficient distributed algorithm for minimum-latency aggregation scheduling in wireless sensor networks[C]. 2010 IEEE 30th International Conference on Distributed Computing Systems (ICDCS 2010), Genova, Italy, June 21-25, 2010: 827-836.
[6]Basagni S. Finding a maximal weighted independent set in wireless networks[J].Telecommunication Systems, 2001,18(1-3): 155-168.
[7]Sakai S, Togasaki M, and Yamazaki K. A note on greedy algorithm for the maximum weighted independent set problem[J].Discrete Applied Mathematics, 2003, 126(2-3):313-322.
[8]Nieberg T and Hurink J. Wireless communication graphs[C].Proceedings of the 2004 Intelligent Sensors, Sensor Networks& Information Processing Conference (ISSNIP 2004),Melbourne, Australia, Dec. 14-17, 2004: 367-372.
[9]Sanghavi S, Shah D, and Willsky A S. Message passing for maximum weight independent set[J].IEEE Transactions on Information Theory, 2009, 55(11): 4822-4834.
[10]Kschischang F R, Frey B J, and Loeloger E A. Factor graph and the sum-product algorithm[J].IEEE Transactions on Information Theory, 2001, 47(2): 498-519.
[11]Bayati M, Shah D, and Sharma M. Max-product for maximum weight matching: convergence, correctness, and LP duality[J].IEEE Transactions on Information Theory, 2008,54(3): 1241-1251.
[12]Sanghavi S, Malioutov D, and Willsky A S. Belief propagation and LP relaxation for weighted mathching in general graphs[J].IEEE Transactions on Information Theory,2011, 57(4): 2203-2212.
