基于快速变极化的认知无线电频谱感知算法

刘芳芳 冯春燕 郭彩丽 魏 冬

(北京邮电大学信息与通信工程学院 北京 100876)

1 引言

频谱感知是认知无线电(Cognitive Radios,CR)研究的核心关键技术，面临的主要问题是如何通过接收并分析无线环境中的信号来判断授权用户是否出现，从而发现频谱空穴。解决该问题的频谱感知算法通常可以抽象为一个“黑盒子”[1]，由接收信号、分析信号以及影响信号分析性能的控制参数三部分组成，其输入与输出分别为无线环境与频谱空穴判决。传统频谱感知算法主要有本地的相干检测、能量检测、循环平稳特征检测和熵检测[2]，引入协作分集机制[3]、序贯检验方法[4]等的合作频谱感知算法，以及利用授权信号统计规律进行的跨层频谱感知算法[5]等。这些算法侧重于对信号进行分析，通过各种控制参数来判断授权用户的频谱使用状况。例如，能量检测需要设置的控制参数为检测门限等，熵检测则需要将信号的频谱熵设为控制参数，基于序贯检验的合作频谱检测所需主要控制参数为参与合作的CR用户数量。事实上，频谱感知算法快速、准确的输出不仅与信号分析方法有关，更从根本上依赖于对无线环境中信号的接收[6,7]。无线信号具有幅度、相位、频率以及极化等多种本质属性，由于不同频段的授权用户具有多样性的授权信号，使得对这些信号的接收成为限制信号分析性能提升的瓶颈，是频谱感知算法的基本问题。

本文关注的就是如何通过识别授权信号的极化状态来优化对信号的接收，提高频谱感知算法黑盒子的输出性能。极化是信号所固有的矢量特性，当授权信号与CR用户接收极化状态相同即匹配时，能够接收授权信号的全部功率；当二者正交即完全失配时，将接收不到授权信号[8]。显然，若CR用户忽略授权信号的极化状态，仅采用固定的接收极化状态对信号进行接收，尤其是完全失配时，无论采用何种信号分析方法，其输出的漏检概率都将大大增加，会严重影响频谱感知算法黑盒子的输出性能，导致对授权用户造成有害干扰。可见，识别授权信号的极化状态在提高频谱感知性能中具有巨大的应用潜力[9,10]，然而现有研究对授权信号这一矢量特性的开发深度和广度还不能与其重要性相称。

对授权信号极化状态的识别本质上是寻找与其相匹配的CR用户接收极化状态，要求CR用户具有变极化功能。根据虚拟极化自适应原理[11]，CR用户采用一对正交极化接收天线，通过对这对天线的接收信号进行幅度和相位加权处理，无需改变天馈系统的参数和状态，采用数字信号处理技术即可实现变极化，能够遍历任意的接收极化状态。为满足频谱感知的实时性要求，本文提出了一种基于K臂赌博机[12]的快速变极化算法(K-armed Bandit based Rapid Polarization Adaptation, KB-RPA)，将极化状态识别中复杂的双自由度搜索问题简化为K个独立的1维问题进行求解，进而利用识别出的极化状态进行匹配接收，以能量检测这一信号分析方法为例讨论了频谱感知性能。

2 信号模型与问题描述

2.1 授权信号极化状态表征

假设授权用户发射的矢量信号表示为Sp，其极化状态记为Xp。根据极化分解原理，Sp可以在任意一组正交极化基上进行矢量分解，不妨采用正交的水平/垂直极化基(h,v)将其表示为

其中Sph和Spv分别代表水平极化基和垂直极化基上的信号分量，i和q分别表示同相分量和正交分量。

Sp的极化状态Xp可用 Jones矢量形式表示为

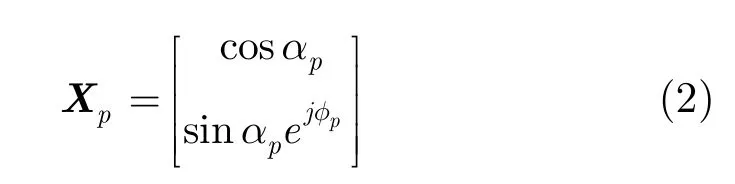
其中(ap,fp) ,ap∈[0,p/ 2],fp∈ [ 0,2p]称为信号的极化相位描述子，有

可以看出，tanap为两个正交极化分量Sph和Spv的幅度之比，fp为它们的相位差，Xp本质上是将Sp进行归一化并忽略绝对相位信息所得到的矢量。

这样，在给定的极化基(h,v)上，授权信号Sp的极化状态Xp能够通过极化相位描述子(ap,fp)进行完全且唯一地表征[9]。

2.2 问题描述

CR用户接收的信号为

其中H0与H1分别表示授权信号不存在和存在的两种假设；G表示授权用户与CR用户之间的复2维无线信道增益矩阵，这里假设信道特性理想，即G为 2维单位矩阵；W表示均值为零、方差为s2的复高斯噪声，其协方差矩阵为ΛW=s2I2，这里I2表示2维单位矩阵。

CR用户以极化状态Xs(as,fs)对R进行接收，其中(as,fs)为Xs的极化相位描述子，将R到达CR用户接收天线时的信噪比记为g0，实际接收的平均信噪比g为

其中上标H表示复共轭转置，E{·}表示取均值。需要指出的是，复高斯噪声W是具有时变随机极化状态的未极化波，采用任意Xs, CR用户对W的平均接收功率均是确定的，有

对授权信号Sp的接收功率，取决于Xs与Xp之间的极化匹配系数m(Xs,Xp)

将式(6)和式(8)代入式(5)，有

已经证明，当且仅当Xs=Xp时，表示Xs与Xp极化匹配，有m(Xs,Xp) = 1，这意味着CR用户可以接收其天线处的授权信号的全部功率，获得最大化的平均接收信噪比gmax=g0，即

对于CR用户来讲，通过变极化来改变Xs，如果能够获得对授权信号的最大平均接收信噪比gmax，即可根据式(10)识别出授权信号的极化状态Xp。这样，对授权信号极化状态的识别问题实质上是CR用户通过变极化来搜索gmax所对应的Xs，可以描述为

在极化基(h,v)上，当极化相位描述子(as,fs)遍历([0,p/ 2],[0,2p])时，CR用户可实现对所有极化状态的变极化，这是一个双自由度搜索问题[9]。若分别取as和fs的个数为N，其复杂度为O(N2)。

3 极化状态识别KB-RPA算法

实际中，为了进行实时的频谱感知，通常要求CR用户能够快速地对授权信号极化状态进行识别。本文所提出的KB-RPA算法主要目的就是为了将上述复杂的双自由度搜索问题转化为K臂赌博机问题，通过求解K个独立的1维问题，使得授权信号极化状态识别算法的复杂度显著降低为O(N)。

3.1 算法设计

在原始的K臂赌博机问题中，有一个拥有K个手臂的投币机器。赌博者每次选择K个手臂中的一个进行操作来得到相应的收益(正值、零或负值)，其目的就是在一个特定的时间段内最大化总收益。由于每个手臂都假设有不同的收益的分布，算法终止时赌博者会发现使自己获得最大收益的手臂，并用这个手臂进行赌博[12]。

3.2 算法步骤

本文KB-RPA算法的主要步骤描述如下：

(1)初始化 选取K组不同取值的极化描述子 { (as1,fs1),… ,(asK,fsK)}，其中手臂k对应 CR用户的一个接收极化状态Xsk(ask,fsk)。

令L表示赌博机要执行的最大步数；l表示当前赌博机执行的步数；rk(l)表示前l-1步选择手臂k的收益累计和。

初始化循环次数l= 1 , 1 ≤l≤L，并有rk(1)= 0 。

(2)分布估计 以制约因子w＞ 0 来确定选择手臂k的概率dk(l)，估计分布向量d(l) = [d1(l),…,dK(l)]。

对于dk(l)，有

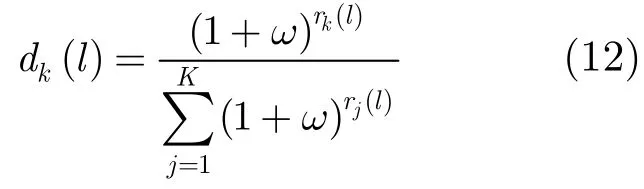
(3)分布叠加 这一步主要是为了排除由于对手臂k选择的次序不同而带来的不稳定性，使得算法对K个手臂均能有所选择，以获得较好的分布估计性能。

将式(12)所得到的概率分布dk(l)与均匀分布以制约因子m∈ [ 0,1]进行叠加，得到叠加概率(l)，有

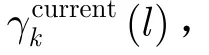
那么，手臂kcurrent(l)的当前收益记为

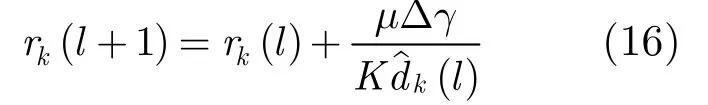
K个手臂的收益累计和可分别更新为

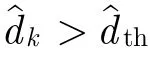
(6)当赌博机满足终止条件时，选择收益累计和rk最大的手臂

3.3 算法理论分析

制约因子w和m的选择分别决定了分布向量d(l)和叠加分布向量(l)的取值，而且在臂数K一定的情况下共同制约着 KB-RPA算法预期收益的边界取值，对KB-RPA算法的性能有重要的影响。令表示在L次操作中选择最优手臂kbest进行接收的收益累计和，根据文献[12]中的定理4.1, KB-RPA算法对K个手臂的预期总收益满足

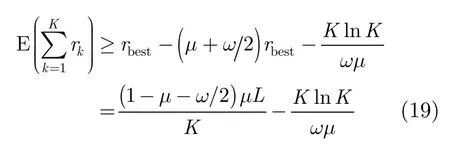
此外，由于KB-RPA算法采用式(13)来选择CR用户接收极化状态所对应的手臂，对于平均接收信噪比累积收益较大的手臂，其选择的概率也较大，并且会随着赌博机的进一步运行而不断增大，最终显著地收敛于拥有最大信噪比的接收极化状态。但是收敛后选择的手臂所对应的接收极化状态受限于K的取值，例如，当K=1时，意味着CR用户采用特定的极化状态接收，失去了变极化的物理意义，无法识别授权信号极化状态；当K→∞时，意味着 CR用户能够遍历所有的接收极化状态，得到授权信号极化状态识别的全局最优解，识别精度即对授权信号极化状态识别的准确程度达到最优，但是算法计算复杂度急剧增加，成为一个NP问题。实际中通常需要对授权信号极化状态识别精度与识别算法的复杂度进行折中。

4 基于KB-RPA的频谱感知

构造能量检测的判决统计量Y为

其中T为抽样数。设l为能量检测的判决门限，有

则检测概率Pd和虚警概率Pf可分别表示为[13]

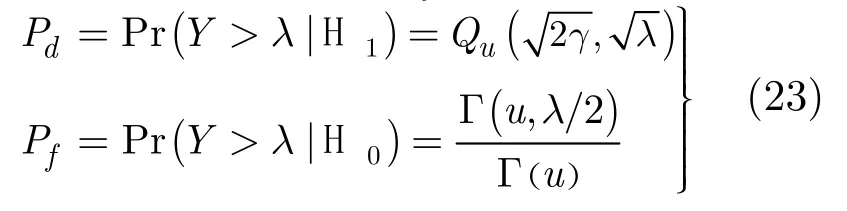
其中u是时域带宽积，与抽样数T成正比；Qu为广义 Marcum Q 函数； Γ(·)和 Γ(·,·)为完全和不完全的Gamma函数。

值得注意的是，CR用户通过识别授权信号极化状态，能够优化对授权信号的接收，这里对能量检测的讨论可以推广到其它检测算法场景。由于充分保留了授权信号的能量、相关性以及循环平稳性等特征，基于KB-RPA算法的频谱感知能够改善CR用户对授权信号的分析能力，有效提高频谱感知性能。

5 仿真分析

首先分析 KB-RPA算法的收敛性和计算复杂度。(1)对于不同臂数K，若不考虑噪声，CR用户采用 KB-RPA算法对授权信号的接收功率随算法运行步数的变化如图 1所示。K分别取(2,4,6,8)，算法均能够收敛于取得最大接收功率的手臂，对应的最大接收功率分别为(0.5,1,0.9593,1)。特别地，当K=4和K=8时，由于存在与Xp匹配的手臂，接收功率可以收敛于最大值1。K=6时，由于KB-RPA算法能够采用更多不同的接收极化状态Xs进行识别，接收功率也达到了0.9593。可见，算法收敛时对授权信号的接收功率与臂数K的大小以及各臂对应的极化相位描述子{(as,φs) }K的取值密切相关。随着K增大，接收功率收敛所需要的算法运行步数不断增加，分别为(3 2, 66, 151, 648)，意味着算法的计算复杂度也随之增加。(2)若考虑噪声的影响，取CR用户接收天线处信噪比g0= 2 0 dB，通过重复运行KB-RPA算法并取平均，可获得不同臂数K下对同一授权信号的平均接收信噪比，图 2所示为算法运行200次后得到的结果。与图1中的接收功率分析类似，随着算法运行步数不断增加各平均接收信噪比趋向于稳定，说明算法能够收敛。当K=2和K=6时，平均接收信噪比均低于 20 dB；而K=4和K=8时，平均接收信噪比均趋向于20 dB，能够较好地保留授权信号的功率信息。然而K=8时的收敛速度比K=4时低83.3%。

其次分析KB-RPA算法的识别精度h。受实际中噪声不确定性的影响，h采用算法收敛时的平均接收信噪比g与CR用户接收天线处信噪比g0的比值来表征，即

h越接近1越能够保留授权信号完整的幅度、相位等信息，说明识别精度越高。表1中列出了不同g0和K取值下的算法识别精度h。在同一g0情况下，K=4的算法识别精度比K=2时至少高46.46%。若K不变，随着g0的增加，算法识别精度也不断增加，意味着噪声对算法的影响逐渐减小。在低信噪比情况下，KB-RPA算法仍然能保持较好的识别精度性能。

表1 算法识别精度η

图1 不同臂数K下对授权信号的接收功率

图2 不同臂数K下对授权信号的平均接收信噪比

下面讨论基于KB-RPA算法的频谱感知。不同臂数K情况下能量检测的接收机操作特性曲线(Receiver Operation Characteristic, ROC)如图 3所示。令 CR用户接收天线处信噪比g0=10 dB，且取抽样数T=1，即 CR用户将 KBRPA算法每一步运行得到的功率与检测门限进行比较，并采用蒙特卡罗方法以克服噪声的随机性影响。可以看出，当K=4时，KB-RPA算法能够快速收敛并以授权信号极化状态Xp的匹配极化进行接收，检测性能优于K=2与K=6的情况。K=8时也存在与Xp相匹配的极化状态，检测性能同样优于K=2与K=6的情况；但由于臂数增加引起算法复杂度提高，在算法运行过程中检测性能低于K=4，一旦算法收敛，则可以与K=4收敛于相同的极化状态接收信号并获得同样的能量检测性能。当K=6时，对授权信号的平均接收信噪比优于K=2的情况，但收敛所需步长较K=4时增加，能量检测性能取得了折中。

进一步地，比较所提变极化匹配接收与其它三种固定极化接收所获得的能量检测性能，相应的ROC曲线如图4所示。这三种固定极化接收方法即分别采用水平极化或垂直极化的单一极化接收方法，以及结合水平极化与垂直极化的双天线联合接收方法。这里双天线联合接收是指将分别采用水平极化天线和垂直极化天线接收的信号功率相加求和进行能量检测判决。在相同的噪声环境下，由于授权信号与水平极化、垂直极化的极化匹配系数分别为0.9239与0.3827，采用水平极化接收的能量检测性能要优于垂直极化接收。而双天线联合接收可以利用两个天线上的信号接收功率，能量检测性能优于水平或垂直单一极化接收。而KB-RPA算法能够利用水平与垂直极化基上极化分量的相关性进行匹配接收，与双天线联合接收相比，能量检测性能提升。可见，CR用户通过优化接收极化状态，可增大与授权信号的极化匹配系数，提高检测概率Pd，从而显著提高频谱感知性能。

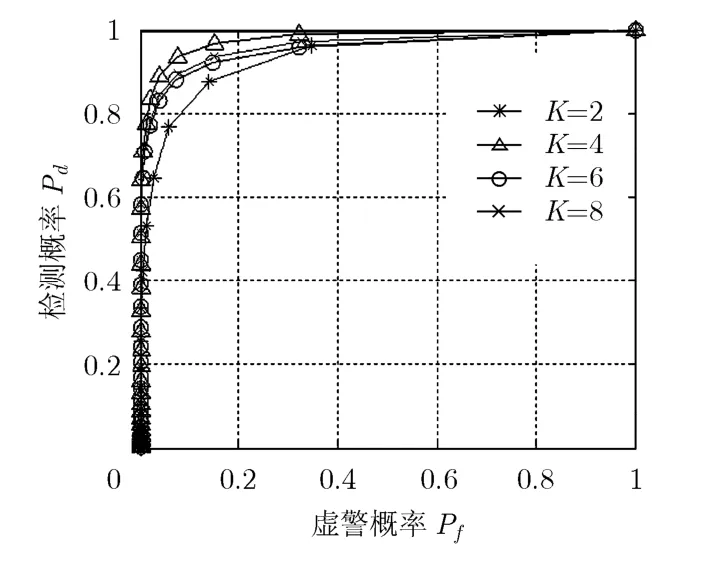
图3 不同臂数K下能量检测ROC曲线(g0 = 1 0 dB )

图4 不同信号接收方法的能量检测ROC曲线(g0 = 1 0 dB )

6 结束语

极化状态作为信号的本质属性，包含了丰富的授权信号矢量信息，对CR用户增强频谱感知性能并提高频谱利用率具有重要意义。为充分利用授权信号这一矢量特性，本文提出了一种基于K臂赌博机的快速变极化算法来识别授权信号的极化状态。若极化识别过程中授权用户的极化状态不发生改变，采用该算法可大大简化极化状态识别中的双自由度搜索过程，能够迅速收敛，并保证以较低复杂度实现对授权信号极化状态的高精度识别，识别精度受无线环境信噪比恶化影响较小。进而通过理论分析讨论了制约因子w和m的选取，并给出了KB-RPA算法预期收益的边界取值。最后以能量检测为例，阐述了识别授权信号极化状态对频谱感知性能的影响。仿真结果表明，采用 KB-RPA算法识别授权信号极化状态，能够快速有效地提高与授权信号的极化匹配系数，对能量检测的性能提升显著。在后续研究中，将就极化状态在频谱感知中衰落信道环境下的更多潜在应用展开深入分析与讨论。

[1]Yucek T and Arslan H. A survey of spectrum sensing algorithms for cognitive radio applications[J].IEEE Communications Surveys&Tutorials, 2009, 11(1):116-130.

[2]Xia Hong-xing, Zhang Guo-ping, and Ding Yao-ming.Spectral entropy based primary user detection in cognitive radio[C].IEEE WiCom 2009, Beijing, Sep.24-26, 2009: 1-4.

[3]Zhao Guo-dong, Ma Jun, Li G Y,et al.. Spatial spectrum holes in cognitive radio with relay transmission[C].IEEE VTC 2009 Spring, Barcelona, Apr. 26-29, 2009: 1-4.

[4]Chaudhari S, Koivunen V, and Poor H V.Autocorrelation-based decentralized sequential detection of OFDM signals in cognitive radios[J].IEEETransactions on Signal Processing, 2009, 57(7):2690-2700.

[5]Kae W C. Adaptive sensing technique to maximize spectrum utilization in cognitive radio[J].IEEE Transactions on Vehicular Technology, 2010, 59(2):992-998.

[6]Liu Fang-fang, Feng Chun-yan, Guo Cai-li,et al.. Virtual polarization detection: a vector signal sensing method for cognitive radios[C].IEEE VTC 2010 Spring, Taipei, May 16-19, 2010: 1-5.

[7]Wei Dong, Guo Cai-li, Liu Fang-fang,et al.. A SINR improving scheme based on optimal polarization receiving for the cognitive radios[C]. IEEE IC-NIDC 2009,Beijing, Nov. 6-8, 2009: 100-104.

[8]Stapor D P. Optimal receive antenna polarization in the presence of interference and noise[J].IEEE Transactions on Antennas and Propagation, 1995, 43(5): 473-477.

[9]庄钊文, 肖顺平, 王雪松. 雷达极化信息处理及其应用[M].北京: 国防工业出版社, 1999, 第2章.

[10]Liu Fang-fang, Feng Chun-yan, Guo Cai-li,et al..Polarization spectrum sensing scheme for cognitive radios[C]. IEEE WiCom 2009, Beijing, Sep. 24-26, 2009:1-4.

[11]Poelman J. Virtual polarisation adaptation: a method of increasing the detection capability of a radar system through polarisation-vector processing[J].IEE Proceedings of Communications, Radar and Signal Processing, 1981, 128(5): 261-270.

[12]Auer P, Cesa-Bianchi N, Freund Y,et al.. Gambling in a rigged casino: the adversarial multi-armed bandit problem[C]. 36th Annual Symposium on Foundations of Computer Science, Milwaukee, Oct. 23-25, 1995:322-331.

[13]Dongliang D, Liuqing Y, and Principe J C. Cooperative diversity of spectrum sensing for cognitive radio systems[J].IEEE Transactions on Signal Processing,2010, 58(6): 3218-3227.