基于滑窗MCMC的弹道导弹分导团目标数据关联研究

俞建国 刘 梅 王 骏

①(哈尔滨工业大学电子与信息工程学院 哈尔滨 150001)

②(中国电子科技集团第29研究所 成都 610036)

1 引言

弹道导弹(Ballistic Missile, BM)在现代战争中具有穿透力强，威慑力大等特点，是各国空间预警和监视系统重点关注的目标。BM 为了提高突防能力，在再入过程中往往伴随着多弹头分导技术，并且在多批次饱和攻击模式下，密集程度较高，与传统多目标数据关联[1,2]相比，对分导弹头数据关联难点在于：(1)分导弹头数目以及分导时间未知，弹头之间距离较小，速度非常相近，易于形成团状；(2)弹头再入速度大，距离打击目标近，拦截时间短。因此，必须寻求新的数据关联方法用于解决弹道导弹分导特定应用背景问题。

目前运用较为成熟的多目标数据关联方法为贝叶斯类数据互联。贝叶斯典型方法包括单步贝叶斯和多步贝叶斯方法。单步贝叶斯方法只对最新的量测集合进行关联，是一种次优贝叶斯方法，比较有代表性的算法有最近邻[3](Nearest-Neighbor, NN)和联合概率数据互联算法[4](Joint Probability Data Association, JPDA)。NN方法在目标密集、数量变化以及有杂波和漏警的环境下效果难以令人满意，而JPDA计算关联概率权值是个NP-hard问题。这两种方法都不能处理目标建航和航迹撤销问题。多步贝叶斯方法对当前时刻以前的量测值进行研究，给出每个量测序列的概率，以多假设跟踪[5](Multiple Hypothesis Tracking, MHT)算法最具代表性。它通过对当前时刻之前的量测序列进行假设关联，返回最大后验概率的假设关联作为最优关联，是目前多目标关联应用较为成熟的算法。它能够解决不定数目的目标建航和终结问题，不足之处是通过枚举的方法获得所有关联假设，计算量较大。

在此应用背景下本文提出了一种改进的实时滑窗 MCMC方法用于解决弹道导弹分导数据关联问题。该算法将弹头分导视为平稳的马尔可夫过程，通过蒙特卡洛采样的方法对监控区域的测量集合进行组合优化，获得最大的后验概率密度进而逼近马氏链的平稳分布，结合弹头分导的实际应用背景进行继承性优化以及关联假设概率权值重新分配，在保持较高的关联概率下极大地提高了实时性。

2 滤波状态方程与测量方程

2.1 状态方程

弹道目标的作战窗口一般在被动段，因此本文所用的滤波模型主要针对弹道目标的被动段，用f表示。BM 在被动段主要受地球引力、大气阻力以及惯性力作用，这里惯性力包括科里奥利力和向心力。考虑地球的椭球性，保留球引力二阶以下带谐项，结合BM在该阶段所受的4个力可得到地心固连参考坐标系(Earth-Centered Earth-Fixed, ECEF)下的6个常微分方程用于描述被动段模型[6,7]，方程组如下：

式(1)中m为导弹质量，x,y,z和vx,vy,vz分别代表导弹在ECEF坐标系下的3个方向的位置和速度，x,y,z分别为3个方向位置单位矢量，Fg为重力，具体表达式可参考文献[8]。||˙||为速度幅值，ω为非惯性坐标的自转角速度大小为 7 .292115 × 10-5rad/s。β为质阻比，表征弹头在再入过程中速度衰减快慢的物理量，一般与弹道目标的质量和几何形状有关，在再入过程中是变化的，因此将其作为其中的一个状态变量进行估计。ρ(h)为空气密度，与当地的海拔高度h有关，本文采用美国标准大气层模型1976(USSA1976)。

假设第k时刻系统状态向量为X(k)=[x(k),vx(k),y(k),vy(k),z(k),vz(k),β(k)]T，对其离散化可得状态方程如式(2)所示。

其中F为状态转移矩阵，G为输入控制矩阵，u(k)为加速度控制项，它由式(1)确定，V(k)为各状态变量对应的过程噪声，这里认为它服从零均值的高斯分布，协方差为 0 .01·[I7×7]。F,G表达式可参考文献[9]。

2.2 测量方程

假设目标被地面雷达站所捕获，则获得的数据应为天东北坐标系(Up-East-North, UEN)的观测值Z=[r,a,e]T，其中r为目标与雷达站之间的距离，a和e分别为站心坐标下方位角和俯仰角。为了后续统一处理的方便，将UEN下的测量值转换到ECEF坐标下[6,10]，获得坐标变换后测量值ZTrans=[x,y,z]T,这样便能获得线性的观测方程如下：

H为测量矩阵，W(k+1)为测量噪声，不同坐标系测量噪声的转换过程可参考文献[10]，至此完成了状态方程和测量方程的建立。

3 滑窗MCMC问题描述及算法实现

3.1 后验概率模型

以面向测量数据为指导思想，多目标数据关联问题就是将测量集合进行划分，进而获得后验概率密度最大的组合。

令Z(t)={zi(t):i=1,…,n(t)}为t时刻雷达所获得的目标测量值，则t0时刻之前所有的测量集合为= {Z(t) :1 ≤t≤t0}。令Ω为所有可能的关联组合空间，对于其中任意一个关联假设w∈Ω，对它进行如下约束：

(1)w= {τ0,τ1, … ,τk}，其中τk为第k个子集划分，即由相应的测量集合构成了第k条航迹。因航迹是由测量值集合经过滤波获得，若不加特别说明本文中航迹与相应的测量集合等价；

(3)τ0代表一组虚警；

(4)|τi∩z(t) |≤1,i∈ [ 1,k],t∈ [1,t0]；表明每个测量点迹只能属于其中的一条航迹或者属于虚警；

(5)|τi|≥ 2 ,i∈[1,k]，表示|τi|航迹的长度至少为2，否则无法与测量点迹区分。

对于一个给定的假设关联w，虚警τ0和真实航迹组合{τ1,… ,τk}被完全确定，后续便可对每条航迹进行状态估计。通过贝叶斯准则，对于一个给定的假设关联组合w在已知测量集合Zk的前提下，它的后验概率P(w|Zk)的表达式如下：

P(Zk)表示测量集合Zk出现的概率，表达式与场景具体参数相关，如检测概率(PD)和监视空域内虚警目标个数(假设它满足均值为λV的泊松分布)等，具体可参考文献[11]。P(Zk|w)为关联组合w对测量集合Zk的似然函数，可以通过动力学方程和测量模型表达如下：

式(5)表示关联组合中所有真实航迹的似然函数之和，其中C为归一化常值，|τ|为航迹长度，并且认为航迹是满足以其滤波值为均值，误差协方差为方差的高斯分布。通过式(4)和式(5)便可得到后验概率P(w|Zk)的解。在给定测量集Zk的前提下，寻找最大后验概率的关联假设w等价如下：

求解式(6)所得的关联组合w即为多目标跟踪中点迹航迹关联的解。

3.2 MCMC原理

Bergman等人[12]于2000年首次将MCMC 算法应用于多目标跟踪，Oh Songhwai等人[11,13]进一步提出了详细的关联假设步骤，后续的研究大多集中于静态的全局关联实际应用[14,15]，并未对MCMC关联算法的动态继承性以及实时性进一步研究和阐述。

MCMC是一种从分布为π的状态空间Ω采样构造一个马尔可夫链M(其状态w，服从平稳分布π(w) )的方法。如果当前的关联状态为w∈Ω，则提出的假设关联w'∈Ω服从提议分布q(w,w')，其接受概率为A(w,w')由Metropolis Hastings方法获得。

如果新的关联假设被否定，则保持上一次关联状态w。若M具有不可约性和非周期性，由各态历经定理可知M收敛于其平稳分布π(w)。因此，对于任意给定的一个有界函数f，采样状态经过f作用后的统计均值可通过E(f(w) )来逼近。

MCMC算法的流程如下：

(1)输入测量集合Zk，蒙特卡罗仿真次数mc，任意给出初始关联w=winit;

(2)由提议分布q(w,w')得到一种尝试关联组合w'；

(3)生成U(0,1)随机数u，若u≤A(w,w')，令w=w'，，否则回到步骤(2)；

(4)直到mc次循环完成，最终得到的w为最优关联组合。

通过以上算法流程便可得到最优的关联组合。从MCMC算法流程看，它累积了足够的测量值Zk因此比单步贝叶斯关联算法如 NN关联正确率更高，同时每次关联只需保存最优的关联组合，与多步贝叶斯关联算法MHT相比，能节约大量存储空间和运行时间。

提议分布q(w,w')表示两个关联组合w和w'通过单步变化所构成的操作组合[11,13]，主要包括新航迹的产生，老航迹的终结以及航迹更新等等。

3.3 滑窗MCMC算法实现

传统的 MCMC算法对于处理静态的测量集合具有很好的效果，但对于实时的动态变化的测量集还存在着许多未解决的问题。首先是实时性问题，随着测量数据的增加，如果采用全局测量数据进行组合会出现“组合爆炸”的情况；其次是关联组合的继承性和关联假设概率分配问题，一方面要考虑关联的正确率，另一方面要减少不必要的关联假设的次数。根据“分导”这一物理背景对传统的MCMC算法进行加窗改进，包括关联组合继承性以及关联假设的概率分配，继承性改进示意如图1所示。从图中可见，k时刻在观测扫描窗口[Tk,Tk+Win]内测量集合最优组合为w', Win为时间窗口的大小，下一时刻时间窗口滑至[Tk+1,Tk+1+Win]，选择w2=w'-w1作为下一时刻马尔可夫链的初始状态，这里w1表示在时间窗[Tk,Tk+1]内w'的子集，在剔除w1的同时将新的测量值Znew加入滑窗集合，即

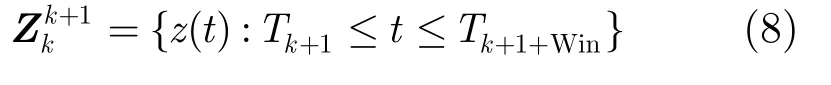
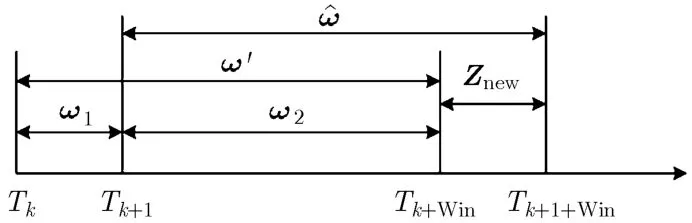
图1 滑窗MCMC算法继承性示意图

通过上述处理，将测量集合按窗口进行划分，类似于降维处理，减小关联组合数量，同时将上一窗口的最优关联组合遗传给下一个窗口作为新的马尔可夫链的初始状态，能够使其快速逼近稳态分布。

另一方面，传统的 MCMC算法对于提议分布中的关联假设是按等概率均匀选取的，而针对本文的弹头分导问题，很明显航迹的产生的概率是最大的，而消亡则相对较小，相应地将航迹产生概率调整为其它假设的2倍，使它更接近真实物理场景，快速达到平稳分布。

4 仿真结果与分析

为验证本文所提出的滑窗 MCMC算法的有效性，设计了相应的仿真场景，分析了分导前后关联正确概率以及运算时间，并在同等条件下比较了MHT方法效果，验证了本文所提出的算法的优越性。

本文所采用的滤波器为 UKF[16](Unscented Kalman Filter)，滤波初始状态Xinit可用前两个时刻的测量值进行确定，即

其中x,y,z为初始位置测量值，Δt为采样间隔，β0为先验的质阻比值，当目标为近中远程弹道导弹它的量级分别为2000 kg/s2, 5000 kg/s2和8000 kg/s2。初始协方差求解可参考文献[10]，滑窗长度选择要在关联正确率和关联时间折中，实验中发现窗口长度大于5个采样周期代价函数可靠性较好，因此本文滑窗长度取 5，即统计结果从第 5个采样点开始计算。

本文所有仿真实验均在Matlab7.0软件平台，以及CPU为AMD Athlon 3000+，内存为DDR400 1 G的硬件平台实现。

4.1 仿真场景设置

本文模拟某中程弹道导弹轨迹建模，导弹再入高度为70 km，在再入10 s后进行弹头分导，持续跟踪 50个采样周期。假设雷达测距噪声标准差为300 m，方位角和俯仰角测量噪声标准差均为 0.1 mrad，服从均值为零的正态分布，采样间隔Δt=1 s。仿真参数选取参考美国太平洋靶场实验的地基雷达在跟踪战术弹道导弹的工作参数[17]。为更真实地模拟弹头分导的实际情况，设置了3种不同的仿真场景分别为稀疏、密集以及异常密集场景，每个母弹头随机分出0～2个子弹头。多批次弹道航迹的产生过程如下：以标准弹道再入点的状态为中心，分别在3个方向的位置和速度加上2000 m和100 m/s高斯分布的噪声作为其余弹道的初始状态，并通过式(1)外推获得真实轨迹。分导弹头位置继承母弹头的位置，在速度上以母弹头速度为基础，分别受到150 m/s, 75 m/s和75 m/s为标准差的高斯分布零均值的随机速度冲量，这样分导弹头既能够保证位置的连续性，同时也能够与母弹头分开，在一定程度上反应了分导的物理过程。

4.2 结果与分析

因弹头分导数目未知，很难对跟踪航迹的位置和速度进行均方根误差统计。本文主要以关联正确率以及计算时间来评价算法的优劣。关联正确率定义如下：

平均关联正确率则为跟踪时间内关联正确率的均值，仿真中涉及的参数有检测概率PD，虚警数目λV以及蒙特卡洛仿真次数mc。

实验1(稀疏场景PD=1，λV=0， mc=500)：再入弹道目标为10个，再入10 s后每个母弹头随机产生0～2的分导弹头，最终得到17个弹道目标，仿真场景以及全局关联概率如图2，图3所示。

从图3可看出，在该场景下，两种算法均能得到较高的关联正确概率，大约在92%以上。整体上MHT算法略优于滑窗MCMC，因为在该场景中分导弹头数量较少，由分导产生的交叉平行等系统干扰较小，次优的滑窗 MCMC只对扫描窗内的数据进行关联，而 MHT则是进行全局关联，充分利用了所有的测量信息。但 MHT算法波动较大，稳定性不如滑窗MCMC。MHT和滑窗MCMC计算时间分别为35 s与22 s，处于同一量级，MHT计算量稍大。由于该场景目标较少，分导后对两种算法的关联正确率影响并不明显，仿真结果也验证了在系统干扰较小的时候全局最优算法具有较好性能。

实验2(密集场景PD=1,λV=0, mc= 1000)：再入弹道目标为30个，分导参数设置不变，最终得到57个弹道目标，仿真场景以及全局关联概率如图4，图5所示。

图2 稀疏仿真场景

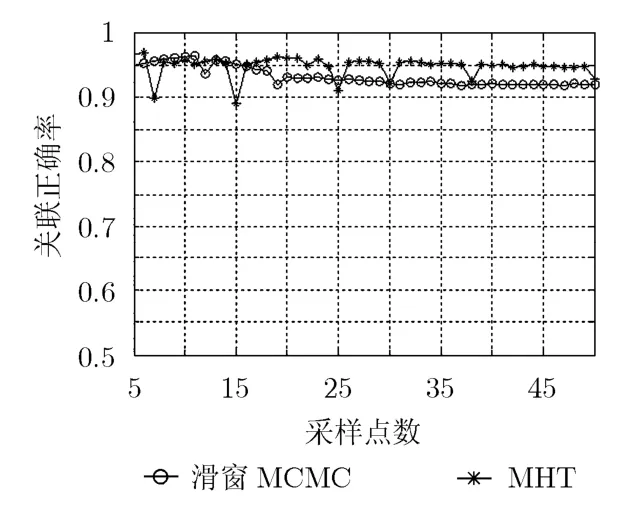
图3 稀疏场景全局关联正确率

图4 密集仿真场景

从图4可见，该场景在分导后有较多的交叉现象，场景比较复杂。从图5看出该场景下滑窗MCMC算法显示出明显的优势，关正确率保持在0.9左右，而MHT则在0.85左右，并且前者具有更好的稳定性。分导后，两种算法的关联正确率都有不同程度的下降，MHT更为明显，正确率下降至0.7左右。分导结束后，随着时间增加，目标数目趋于稳定，相互之间相关性变弱，两种算法的关联正确率逐步恢复至正常水平。在该场景中，MHT和滑窗MCMC运行时间分别为492 s与117 s，滑窗MCMC实时性明显优于MHT。这说明了最优估计算法虽然能最大程度地利用了测量信息，但存在以下两方面不足：第一是计算量大；第二是对未知的系统干扰非常敏感。该结果验证当未知系统干扰过大，最优估计算法性能难于保证。

实验3(异常密集场景PD=1,λV=0, mc=1000)：再入弹道目标为100个，分导参数设置与前面实验相同，最终得到193个弹道目标，仿真场景以及全局关联概率如图6，图7所示。

从图6可见，该场景目标密集程度非常高，特别是在分导后，目标数量几乎增加了一倍，并且交叉现象非常严重，属于复杂场景。分析图7可得到，在发生分导后，两种算法的关联概率都有明显下降，滑窗MCMC降至0.8左右，而MHT则达到0.6。随后滑窗MCMC较快恢复至正常水平，而MHT正确率则不断振荡，经过12 s延迟后才达到正常水平，稳定性比前者相差较大。滑窗 MCMC关联正确率大多保持在 85%以上，而 MHT明显低于滑窗MCMC。而在该仿真场景下，MHT运行时间到达8914 s，而滑窗 MCMC为478 s，几乎相差20倍，实时性明显优于MHT。导致两种算法性能差别的原因与实验2类似，不过多阐述。

针对某一确定的场景，选择不同的检测概率和虚警数目参数对算法性能影响不同，采用某一固定的参数得出的结论并不全面，因此前3个实验均认为检测概率为1，虚警数目为0，专门增加了实验4，选择密集场景，针对不同的检测概率和虚警数目进行平均关联正确率的统计，探讨不同检测概率和虚警数目下两种算法的性能。

实验4(密集场景)：场景设置与实验2完全一致，得到在不同检测概率PD和虚警数目λV下的关联结果如图8，图9所示。

从图 8可看出，不同检测概率下滑窗 MCMC获得的平均正确关联概率均比 MHT要高，同时两种算法的关联正确率都随着检测概率的增加而提高；从图9可见，随着虚警数目的增加，滑窗MCMC与MHT关联效果均下降，MHT下降速度远快于滑窗MCMC，当虚警数目大于50, MHT关联正确率小于0.1，而滑窗MCMC还保存在0.4以上，这说明了在恶劣环境下滑窗MCMC效果优于MHT。

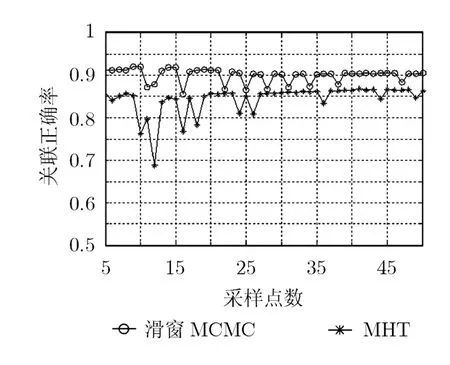
图5 密集场景全局关联正确率

图6 异常密集仿真场景

图7 异常密集场景全局关联正确率

图8 不同检测概率下的关联结果

图9 不同虚警数目下的关联结果

5 结论

本文首先介绍了弹道被动段的动力学特性，对传统的 MCMC算法的继承性及关联假设概率权值进行改进，提出一种改进的实时滑窗 MCMC算法用于解决多批次弹道导弹分导团目标数据关联问题。仿真结果证实，在恶劣环境下，本文所提算法不仅关联概率要高于 MHT算法，并且具有较好的稳定性，更重要的是本文算法的实时性远优于MHT，适用于密集环境下的变数目的实时数据关联。

[1]Hamouda Y E M and Phillips C. Adaptive sampling for energy-efficient collaborative multi-target tracking in wireless sensor networks [J].IET Wireless Sensor Systems, 2011,1(1): 15-25.

[2]Mansouri M, Snoussi H, and Richard C. Channel estimation and multiple target tracking in wireless sensor networks based on quantised proximity sensors [J].IET Wireless Sensor Systems, 2011, 1(1): 7-14.

[3]Li XR and Bar-Shalom Y. Tracking in clutter with nearest neighbor filters: analysis and performance [J].IEEE Transactions on Aerospace and Electronic Systems, 1996,32(3): 995-1010.

[4]Chang Kuo-chu and Bar-Shalom Y. Joint probabilistic data association for multitarget tracking with possibly unresolved measurements and maneuvers [J].IEEE Transactions on Automatic Control, 1984, 29(7): 585-594.

[5]Evangeline P, Benjamin P, and Michele R. Hybrid algorithms for multitarget tracking using MHT and GM-CPHD [J].IEEE Transactions on Aerospace and Electronic Systems,2011, 47(2): 832-847.

[6]Benavoli A, Chisci L, and Farina A. Tracking of a ballistic missile with a-prior information[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 1000-1016.

[7]Minvielle P. Decades of improvements in re-entry ballistic vehicle tracking[J].IEEE Aerospace and Electronic Systems Magazine, 2005, 20(8): Part 1, CF-1-CF-14.

[8]Li X R and Jilkov V P. Survey of maneuvering target tracking. Part II: motion models of ballistic and space targets[J].IEEE Transactions on Aerospace and Electronic Systems,2010, 46(1): 96-119.

[9]权太范. 目标跟踪新理论与技术[M]. 北京: 国防工业出版社,2009: 206-213.

Quan Tai-fan. Target Tracking: Advanced Theory and Techniques[M]. Beijing: National Defence Industry Press,2009: 206-213.

[10]何友, 修建娟, 张晶炜, 等. 雷达数据处理及应用[M]. 第2版.北京: 电子工业出版社, 2009: 35-37, 66-74.

He You, Xiu Jian-juan, Zhang Jing-wei,et al.. Radar Data Process and Application[M]. 2nd Edition, Beijing: Electronic Industry Press, 2009: 35-37, 66-74.

[11]Oh Songhwai, Russell S, and Sastry C. Markov chain Monte Carlo data association for general multiple-target tracking problems [C]. 43rd IEEE conference on Decision and Control,Atlantis, Paradise Island, Bahamas, 2004, Vol.1: 735-742.

[12]Bergman N and Doucet A. Markov chain Monte Carlo data association for target tracking [C]. 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing,Istanbul, Turkey, 2000, Vol.2: 705-708.

[13]Oh Songhwai, Russell S, and Sastry S. Markov chain Monte Carlo data association for multi-target tracking [J].IEEE Transactions on Automatic Control, 2009, 54(3): 481-497.

[14]Lian F, Han C Z, Liu W F,et al.. Sequential Monte Carlo implementation and state extraction of the group probability hypothesis density filter for partly unresolvable group targets-tracking problem[J].IET Radar,Sonar&Navigation,2010, 4(5): 685-702.

[15]齐照辉, 刘雪梅, 梁伟. 基于MCMC的导弹主动段突防仿真及灵敏度分析 [J]. 系统工程与电子技术, 2010, 32(4):803-806.

Qi Zhao-hui, Liu Xue-mei, and Liang Wei. Survival simulation and sensitivity analysis of ballistic missile in boost phase based on MCMC[J].Journal of Systems Engineering and Electronics, 2010, 32(4): 803-806.

[16]Julier S J and Uhlmann J K. A new extension of the Kalman filter to nonlinear systems [J].Proceedings of SPIE, 1997,3068(182):182-193.

[17]Farrell W J. Interacting multiple model filter for tactical ballistic missile tracking [J].IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 418-426.