一种基于RBF神经网络线损计算方法研究

张艳，许哲雄，罗成

(同济大学，上海 201804)

1 引言

在配电网中，由于其电压等级低、直接与用户连接、线路分布广、连接设备多等因素，使得系统存在较大的阻抗，导致电能在转换、输送、分配过程中不可避免地伴随着大量的线路损耗。随着国民经济的发展，用电负荷和用户不断增加，电力系统的网络结构也有所改变。配电网结构的改变、运行变化等使得电能分布不合理，电能质量严重下降同时电能损耗增大。因此准确地计算配电网的线损，并制定降低配电网线损的措施就具有非常重大的意义［1，2］。

人工神经网络［3］具有学习和容错的能力，其计算是并行的，有利于实现实时应用。在神经网络模型中应用最广泛的是BP模型，标准的BP模型使用梯度下降算法训练，但该学习算法收敛速度较慢［4］。

本文所使用径向基函数(RBF)神经网络具有任意函数逼近能力［5］。RBF网络由输入层、隐层、输出层三层组成，隐层节点中的基函数对输入信号局部产生响应，距离基函数中央越近，输出越大，从而使得RBF网络具有极强的局部逼近能力，其网络的学习时间远小于BP神经网络学习算法的训练时间。另外，RBF网络的隐藏神经元数目可以在参数优化过程中自动确定［6］。

本文针对配电网线损计算，详细叙述了基于径向基函数神经网络(RBF)算法的模型、工作原理，并且通过仿真验证了该方法的有效性。将其与分群算法相结合获得了很好的计算精度，提高了实用性。

2 径向基函数神经网络模型

径向基函数网络是一个三层前向型神经网络。其包含线性神经元的输入层节点传递输入信号到隐含层，隐含层节点由高斯函数的辐射状左右函数构成，输出层节点通常是简单的线性函数。

图1是径向基神经元模型，与每个隐含层节点相关的参数向量为ci(即中心)和σi(即宽度)。一般隐含层各节点都采用相同的径向基函数，径向基函数有多种形式，常取高斯函数。

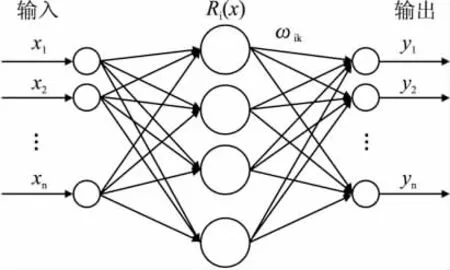
图1 径向基函数神经元模型

网络输入与输出之间可认为是一种映射关系:f(x):Rn→R。

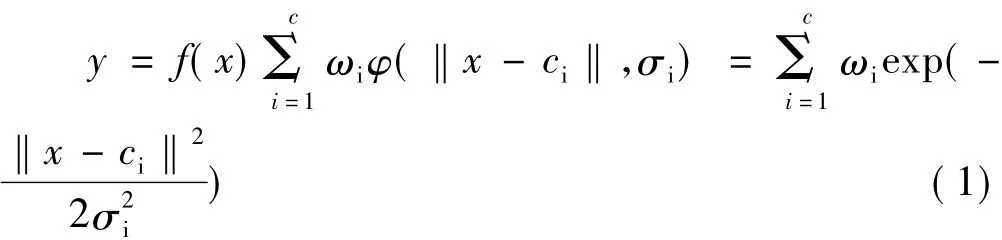
式中，c—隐含层节点数;||·||—欧几里得泛数;x，ci∈Rn;ωi为第i个基函数与输出节点的连接权值(i=1、2、……、c)。构造和训练一个RBF神经网络就是使它通过学习，确定出每个隐含层神经元基函数的中心ci，宽度σi，以及隐含层到输出层的权值ωi这些参数的过程，从而可以完成所需的输入到输出的映射。

假设定义隐含层节点的激活函数是固定径向基函数，中心的位置可以用随机的方式从学习数据集中选取，如果学习样本是以当前问题的典型方式分布的，该方法是较为适合的。特别地，一个以ci为中心的径向基函数定义为:

其中，i=1、2、…、k，k是隐含层节点数，dmax是所选中心的最大距离。可以看出，隐含层节点的宽度都被固定。该式可以保证每一个径向基函数都不会太尖或太平，太尖和太平都应尽量避免。

当因变量(RBF模型的输出量)的数值比较分散(即最大值和最小值相差较大)时，RBF模型难以训练到高精度。将样本基本按因变量的大小排序，则可将因变量数据相差不大的样本分为一群，再针对每一类参数用RBF函数进行配电网线损计算，从而达到提高RBF模型训练精度的目的。因为分群和训练相应的RBF模型的目的是为了利用它们判别样本集中未包括的输电线或样本集中包括的输电线在不同运行条件下属于哪一个群，并计算其相应的线损，其线损(因变量)是待计算的、未知的。

考虑到输电线的线损可认为是四个特征参数的增函数，即:月有功功率供电量、月无功功率供电量、配电变压器总容量、线路总长度。将四个特征参数都较小的本排在前面(反之则排在后面)，则排序结果也该基本上是按线损从小到大排序的。我们定义下述性能指标(Performance Index—PI):

ci为第j个特征参数的权重，表示线损随第j个特征参数变化的快慢程度。当线损随第j个特征参数间的变化关系可认为是一线性函数时，ci可取为其斜率。取ci(j=1，2，3，4)，由(3) 式可看出，四个特征参数都较大的样本，其PI值大，相应的线损也较大。这样各个样本的PI值的大小排序则可达到基本按线损大小排序的目的。排序结果按此方法得到后，人为地将样本顺序分为几个群，显然各个群内样本的线损值比较接近。另外，分群算法PI值的从小到大的顺序没有必要完全反映线损从小到大的次序，只要反映出总体趋势就可以了，因为同一群内样本顺序对RBF模型的学习过程影响不大。

3 径向基函数网络的工作原理

将RBF神经网络用于解决复杂问题时，最重要的一点就是将它映射到高维非线性空间，这样更容易线性可分。假设输出层仅有一个节点，输入层有m个神经元，则神经网络m维的输入空间映射到1维的输出空间，即，S:Rm→R1。可以将映射S想象为一个超平面，神经网络将输入数据先映射到这个超平面上，然后通过线性插值得到最后的输出。神经网络正是通过训练使隐含层实现超平面作用的。因此，实现一个神经网络包括两个阶段:训练阶段和应用阶段，训练阶段也称学习阶段。训练阶段通过己知的输入输出数据对形成一个接近理想的超平面，应用阶段将输入数据映射到在训练阶段形成的超平面上的某一点，然后进行线性加权得到输出。

具体来说，由于隐含层的转换函数为高斯函数，这种非线性变换单元的特点是仅仅对“中心”附近的输入敏感，随着与“中心”距离的加大，非线性变换单元的输出减少到很小的值，可以作为0对待，这就表现为一种“局部敏感性”。而减小的快慢由宽度决定，即宽度越大，减少的越慢，反之宽度越小，则减小的越快。“中心”C代表了比较集中的一组数据的中心值，而这组数据就构成了一个“类”。这样，C代表了输入数据的一种模式。用于神经网络学习的样本数据含有有限个不同的模式，各模式对应不同的中心值。采用一定的数学方法，从输入数据中提取代表不同模式的数据中心，并分配适当的宽度值。由各个数据中心及对应的宽度值，即构成了全部非线性变换单元。非线性变换单元的输出再经过输出层的幅值调整，从而得到期望的输出。实际应用时，映射过程实质就是模式的识别，兴奋提取的过程，而这些模式是在学习中提取并存取起来的。

4 仿真分析

为了验证本文所使用方法的有效性和实用性，以某地区的实际配电网络的68组数据为例进行线损的计算和分析。此68组数据，每组数据包含5个变量:配电网运行数据中月有功功率(×104kW·h)、月无功功率(×104kVar·h)、配电变压器总容量(kVA)、线路总长度(km)分别成为 4 个输入神经元x1，x2，x3，x4，实际线损值(×104kW·h)为输出神经元y。

随机抽取60组数据用于建立未分类的RBF神经网络线损计算模型，剩余的8组用于测试所建未分类的RBF神经网络模型的精确性。经过多次调试，未分类RBF算法的参数为goal=0，加权输入spread=0.009。此时所得仿真线损值与实际线损值相比较结果如图2所示。

图2 未分类的RBF神经网络预测结果

为增加函数精度，将此60组数据经过群分算法分为4组，分别对每一组进行RBF神经网络线损计算建模，共建立4组RBF神经网络。将剩余8组测试数据用原有的分群算法分类，并在相应的类别进行测试。此时所得仿真线损值与实际线损值相比较结果如图3所示。

图3 结合分群算法的RBF神经网络预测结果

由图2和图3可知RBF算法能够比较准确的预测电网线损，证明了该算法的有效性，并且通过图2和图3的比较，可以发现分类RBF算法所测结果的精度明显比未分类的RBF算法所测结果的精度要高。

同时为证明本文所使用的方法的优越性，利用上述60组训练数据和8组测试数据，与线性回归算法和BP神经网络算法进行对比，结果如表1所示。

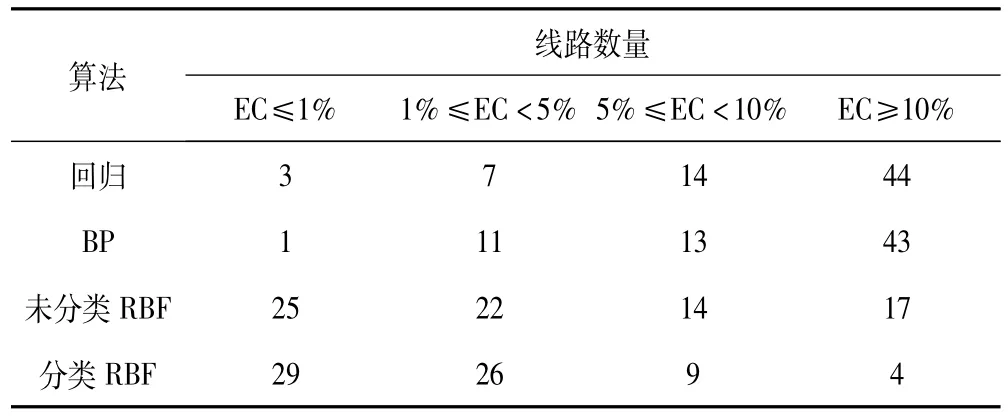
表1 四种算法的结果比较

由表1可以知，回归、BP、未分类的RBF、分类的RBF精确性成递增趋势。其中回归与BP算法相仿，精确性都不如人意，相对误差大于10%的线路条数占了最大的比例。未分类的RBF在精确性上高于前两者，相对误差小于5%的线路条数占了69.1%，但因为无法很好地避免误差大于10%的线路的出现，未分类的RBF算法仍存在应用问题。而分类的RBF算法很好地克服了这一点，68条线路相对误差大于10%的线路仅4条。且精度在5%以下的线路条数比未分类的RBF增长了8条。结合了分群算法的RBF神经网络远优于其他三类方法，从实验仿真角度讲，满足了计算的精度要求。

5 结论

本文针对配电网络线损，研究了基于RBF神经网络算法的线损计算方法。仿真结果证明了该方法的有效性，并且将该方法与分群算法相结合，得到了一种精度更高的算法，实用性大大提高。并且通过4种线损计算方法的比较，突出体现了RBF算法的优越性，特别是与分群算法的结合，线损计算有了进一步的改进，对于配电网络管理与改善有着重要的意义。

［1］袁慧梅.基于GA和ANN的农村中压配电网线损计算研究［D］.1999.

［2］安敏.基于动态自适应聚类算法RBFNN的配电网线损计算新方法［D］.2006.

［3］毕天姝，倪以信，吴复立，等.基于新型神经网络的电网故障诊断方法［J］.中国电机工程学报，2002，22(2).

［4］Tanaka H，Matsufa S，lzui Y，et al.Design evaluation of neural network fault diagnosis［C］.Proceedings of second symposium on Expert system application to power systems，Seattle，1989：378-384.

［5］Simmon Haykin，Neural networks.A comprehensive foundation［M］.New York，Prentice Hall，1999：256-318.

［6］柴杰，江青茵，曹志凯.RBF神经网络的函数逼近能力机器算法［J］.模式识别与人工只能，2002，15(3).