基于小波变换的电力系统谐波检测抗混叠问题研究

龙军，刘俊杰，王冠南，徐鹏

(广西大学电气工程学院，广西 南宁 530004)

1 引言

电网谐波对电力系统安全运行构成潜在的威胁，已被认为是电网的一大公害，不仅给用户和终端设备造成不良影响，而且影响电力测量的准确性，易使继电保护误动作，增加线路和电容器的损耗，降低线路的传输能力，干扰通信等。只有对谐波进行实时监控，准确地掌握谐波的实际情况，才能为谐波治理提供良好依据，便于电网的安全运行。

谐波分析方法主要有傅里叶变换、短时傅里叶变换、Prony分析和小波变换等。传统的傅里叶变换是信号在频域展开，不包含时域信息，不能把时域和频域有机的结合起来，对时变的非平稳信号难以描述，短时傅里叶变换的时-频窗口固定不变，不合适多尺度过程和突变暂态信号分析，Prony分析计算时间太长，很难达到系统实时跟踪要求，小波变换被誉为“数学显微镜”，在时域和频域上窗口满足自适应可调性，具有良好的局部化性质，能对不同的频率成分采用不同的分辨率，聚焦到信号的任意细节，对于检测高频和低频信号均很有效，特别适用于奇异信号和不平稳信号的分析，能准确地反映故障发生的时间、位置等信息。

常用的离散小波快速算法是Mallat算法，由于Mallat算法中小波滤波器的非理想截止特性以及隔点采样和隔点插零，使单个子频带内信号重构产生频率混叠，消除混叠的常见方法有补偿法、内插优化技术以及构建新小波函数等，都引入了大量计算，使得Mallat快速算法计算速度大大下降。本文研究去基波成分的奇抽样小波变换，通过同时抽取奇数坐标和偶数坐标位置的数组元素，分别作插值后将两个结果对应相加，消除混叠分量，同时对基波进行滤除，消除小波变换时基波对谐波计算的影响，此方法对单个子频带内的谐波检测取得了良好效果，计算相对简单，运算量小，增强了谐波检测的实时性。

2 Mallat算法

Mallat算法网络结构图如下:其中h0(n)、h1(n)为分解过程中的低通、高通滤波器，g0(n)、g1(n)为重构过程的低通、高通滤波器，↓2表示下抽样(隔点抽样)，↑2上抽样(隔点补零)，x(n)为原始信号，y(n)为重构信号，a(k)、d(k)为小波分解的近似系数和细节系数，YL(k)、YH(k)为小波重构的近似信号和细节信号，a(k)、d(k)、YL(k)、YH(k)为实际工程应用提供分析依据，在实际工程运用中通过对其修正处理达到待定目的。

图1 Mallat算法结构图

由图1可以看出

3 Mallat算法中的混频现象

根据Mallat分析思想:在小波变换中，将信号分割成不同的子频带信号，不同的尺度体现不同的频率成分，不同的分解水平体现不同的频率变化趋势。Mallat算法将基波信号和谐波信号分解成不同子频带信号时，某些单子频带中会包含其他谐波分量，使得基波分量与各谐波分量或者各谐波分量之间不能有效分离，产生频率混淆现象。

Mallat算法中，下抽样是对偶数坐标的抽取，x(n)→↓2→y(n)的函数表达式为:y(n)=x(2n);此时其z变换为:

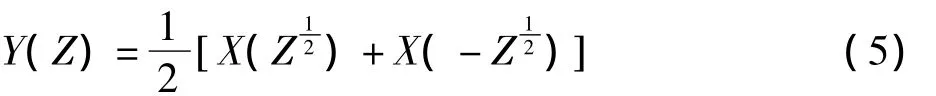
上抽样是对坐标隔点补零，x(n)→↑2→y(n)的函数表达式为:

z变换为Y(Z)=X(Z2)，图1中:

同理，高频部分的信号多项式

式(10)中X(Z)含部分是期望输出，含X(-Z)部分是频率折叠成分。由于小波滤波器的非理想截止特性，加上隔点采样和隔点插零产生的频率折叠，会造成一部分无法抵消的混叠频率。为消除Y(Z)中的混叠频率，学者们提出许多不同的滤波器设计方案，这些方案均要求:

把式(11)代入式(10)，可得到重构信号Y(Z)=H0(Z)G0(Z)+H1(Z)G1(Z[])X(Z)/2。如果同一分解层的小波滤波器h0(n)、h1(n)和g0(n)、g1(n)同时作用，引起频率混叠的分量X(-Z)最终会消除，所以Mallat算法重构原始信号不会出现频率混叠现象，然而式(11)没有保证H0(-Z)G0(-Z)=0和H1(-Z)G1(-Z)=0，由式(8)和式(9)可知，谐波检测时需要提取的单子频带信号YL(k)、YH(k)依然存在X(-Z)分量，会出现混频现象。

4 奇抽样抗混频分析

Mallat算法典型环节中的下抽样是对偶数坐标位置元素的抽取，奇抽样算法加抽取x(n)奇数坐标位置的元素，即设y(n)=x(2n-1)，如图2中虚线所示，x(n)→▼2→y(n)的z变换为:

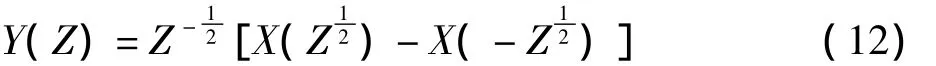
图2 奇抽样序列与原序列关系

图3 Mallat算法添加奇抽样支路基本环节

对a'(n)进行奇数坐标位置元素的抽取得a2(k)，其z变换为:

二插值后得到:

式(16)与式(8)相比，引起频率混叠部分H0(-Z)G0(-Z)X(-Z)/2被消除，细节部分分析同理。

奇抽样小波变换输出结果Y(Z)满足整体抗混叠条件和精确重构条件，同时消除了单子频带中重构信号YL(k)、YH(k)的频率混叠。

5 抗混频谐波检测研究

运用Mallat算法进行电力系统谐波分析时，基波信号的幅值相对较大，其他谐波信号的幅值相对较小，基波对各次谐波的计算会带来较大的影响，严重时会误判频率。针对此问题本文提出了两阶段法解决，第一阶段用奇抽样小波算法对原始信号的概貌进行分析，逐步把基波和各次谐波分离，解决基波成分对各次谐波成分进行小波变换时的影响，减少频谱泄露以及混叠现象;第二阶段对分离出的各次谐波成分进行奇抽样小波变换分析，逐次分离各次谐波，具体如图4所示。

图4 抗混频谐波检测系统原理图

6 Matlab实现

设电网信号基频f=50Hz，采样频率fs=25.6kHz，取点数N=5000，信号中始终含有 3、11、17、43 次谐波，在点n=2000处即t=n/fs=0.07813s时出现基波凸起，在点n=2500处即t=0.09766s时出现5次谐波干扰，设置如下:

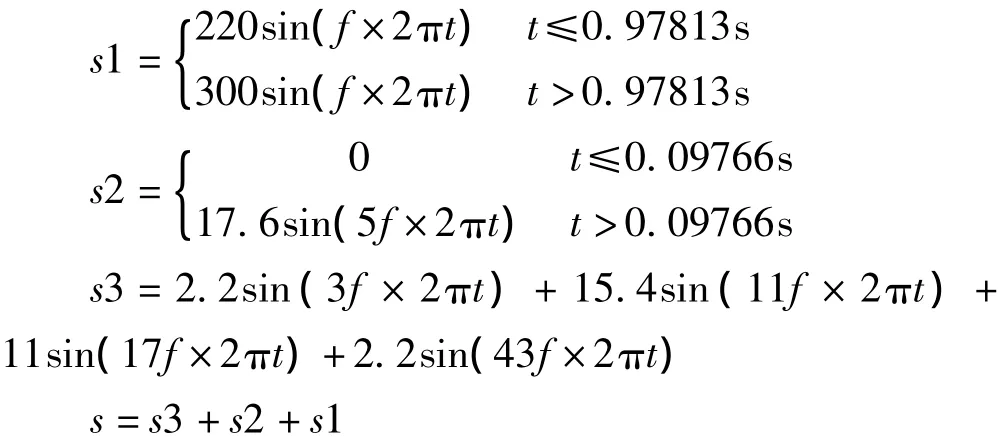
用db24对信号s分别进行传统的小波变换和去基波成分的奇抽样小波变换，分解重构层次为7层，Matlab仿真结果对比如下:

图5～6中深色实线为标准谐波，浅色实线为各层分解信号。a7为小波分解的第七层近似信号，d1～d7为各层的细节信号。容易看出，基波体现在第七层的近似信号a7中，3、5、11、17、43次谐波分别体现在细节信号d7～d3中，d2和d1几乎为零，说明在这两个子频带中没有谐波。由a7、d6信号图可分别算出基波凸起时刻t1=2001/fs=0.07816s和5次谐波产生时刻t2=2495/fs=0.09746s，验证了传统小波变换和去基波成分的奇抽样小波变换都能把信号分解到几个相应的子频带中，实现电力系统谐波检测。

图7和图8为误差对比图，浅色实线为传统小波变换重构单子频带信号产生的误差，深色实线为去基波成分的奇抽样小波变换重构单子频带信号产生的误差，可以看出去基波成分的奇抽样小波变换重构单子频带信号产生的误差相对较小。在点n=2000有基波凸起，综合图5和图6可知滤除基波，可减少基波变化对谐波检测的影响。Matlab仿真表明:采用本文提出的去基波成分的奇抽样小波变换能对原始信号进行分解和重构单支路信号，且误差相对较小。

图5 两种方法重构a7、d7、d6、d5信号

图6 两种方法重构d4、d3、d2、d1信号

图7 两种方法重构原信号的误差对比

图8 两种方法重构各层信号的误差对比

7 小结

奇抽样小波变换加载的抗混叠部分只是奇数抽样和延迟，计算量相对较少，计算速度快，有利于谐波的实时检测。基波分离后再进行奇抽样小波变换能有效的消除基波成分对各次谐波检测时的影响。本文研究的去基波成分的小波变换能将复杂波形的电网信号分解到各子频带中，能在小波域上利用小波分解检测到信号的突变时间及各频率分量有效值和幅度大小，在时域和频域具有良好的局部化特性，对信号分析有高灵敏度和精确性，适用于信号凹陷、信号凸起、短时间谐波及短暂瞬变信号的检测与时频分析，能有效实时地检测电力系统的电压和电流中的谐波含量，可应用于谐波的实时检测和补偿，为电网的谐波治理提供良好依据。

［1］林海雪，孙树勤.电力电网中的谐波［M］.北京:中国电力出版社，1998.

［2］葛哲学，陈仲生.Matlab时频分析技术及其应用［M］.北京:人民邮电出版社，2005.

［3］程正兴，小波分析算法与应用，西安:西安交通大学出版社［M］.1998.

［4］Wagner VE，Balda JC，et al.Effeets of harmonies on equilment，Report of the IEEE Task Force on the Effeets of Harmonies on Equipment.IEEE Transactions on power Delivery，1993，8(2):672-680.

［5］何磊，王泽忠.基于小波算法的电力系统间谐波测量(Measurement of Interharmonics in power Systems based on wavelet transform)［D］.华北电力大学，2006.

［6］吉艳平，危韧勇.基于小波变换的电力谐波［D］.长沙:中南大学，2007.

［7］周厚奎，张昱，金心宇.基于傅里叶和小波变换的电网谐波分析［J］.杭州:电力系统及其自动化学报，2005，17(6):59-62.

［8］柴旭峥，文习山，关根志，等.一种高精度的电力系统谐波分析算法［J］.中国电机工程学报，2003，23(9):67-70.

［9］YOON WEON KI，MICHAEL JDEVANEY.Power measurement using the wavelet transform ［C］.IEEE Instrumentation and Measurement Technology Conference.Saint Paul:IEEE Press，1998:25-33.

［10］郝江涛，刘念，幸晋渝.电力系统间谐波分析［J］.电力自动化设备，2004，12(12):36-39.

［11］胡俊达，张著彬.电力系统中谐波的产生、危害和抑制［J］.湖北电力，2003，27(5):2-4.

［12］周文晖，林丽莉，周兆经.基于小波变化的谐波检测法［J］.仪器仪表学报，2001，22(3):25-29.

［13］杜天军，陈光礻禹，雷勇.基于混叠补偿小波变换的电力系统谐波检测方法［J］.成都:中国电机工程学报，2005，25(3):54-59.

［14］绍明，钟彦儒，余建明.基于小波变换的谐波电流的实时检测［J］.电力电子技术，2000，34(1):42-45.

［15］梁玉娟，李群湛，赵丽平.基于小波分析的电力系统谐波分析［J］.成都:电力系统及其自动化学报，2003，15(6):67-70.