磁管电磁系统与分段磁势电磁系统
2012-07-25左全璋左华京汪昊初
左全璋,左华京,汪昊初
(1.华中科技大学,湖北 武汉 430074;2.广州市地下铁道总公司 广州 510038)
1 引言
双E、双U、螺管等型式的电磁系统,是将衔铁插入线圈内部的电磁系统,是内衔铁电磁系统,过去没有计算它们的磁路的方法。笔者设法将它们的线圈磁势分段,才能获得符合实际的等值磁路图,顺利开展磁路计算。这是一种现将线圈磁势分段,然后又在理论上把分段的线圈磁势,再变为线圈的集中磁势。即先分段再集中,绕了一弯子,解决问题。只有用这种绕弯子的办法,才会有一套螺管电磁系统的磁路计算方法。
螺管电磁系统过去没有正常的磁路计算方法,因为以前都是用线圈集中磁势开始磁路计算,对线圈跨在气隙上的螺管,列不出等值磁路图,当然无法进行磁路计算。一些文献书籍介绍的直接计算螺管电磁系统电磁吸力的公式,是根据电磁吸力公式估算而来的,当然实用性不高。
本文根据笔者了解的背景和已发表的文章的一些要点,阐述这些问题和一些应该注意的特点。
2 交流电磁系统的一种计算方法
以交流接触器为典型电器产品作为研讨的对象。在计算电磁系统时遇到双E型电磁系统。如何计算双E型电磁系统,找不到文献的提示,笔者运用基本原理,设法解决问题,对双E型电磁系统进行剖析。双E型电磁系统的动铁心插入线圈内部。笔者打破常规,将整个线圈的集中磁势剖分为三段,静铁心段、动铁心段、气隙段。这样就可以把磁路各部件的铁磁阻抗在等值磁路图上标注得非常清楚,构成详细等值磁路图,再将等值磁路化简,即将磁阻抗串联或并联,得到具有三段磁势的简化等值磁路图,如图1所示。
整个线圈的匝数为N,静铁心、动铁心、气隙段的线圈匝数分别为N1、N2、N3,即N=N1+N2+N3。两个支路磁阻抗Zm1、Zm2,两个归化漏磁阻Rσφ1、Rσφ2,两个气隙磁阻抗Zδ1、Zδ2,静铁心磁通φ1,动铁心磁通φ2,气隙磁通φ3,构成有三个磁势的简化等值磁路图。仿照电路的回路法,列出一组方程式,可求解φ1、φ2、φ3的数值。

若消去φ1、φ2,求解φ3,并整理,得到一个从未见到过的计算气隙磁通φ3的新公式

这个磁路计算新公式,只有在将线圈磁势被分段的情况下才可能出现。
这个新公式实际上从理论上又将分段磁势的电磁系统转化为线圈集中磁势的电磁系统。由分段磁势IN1、IN2、IN3电磁系统转化为集中磁势IN的电磁系统。转化的办法就是对集中磁势乘以一个线圈磁势修正系数K。这个修正系数K与线圈安装位置和磁路具体情况有关。磁路的总磁阻Zms由两个串联的气隙磁阻抗Zδ1、Zδ2和两个串并联磁阻抗Zm1‖Rσφ1、Zm2‖Rσφ2构成。
3 直流螺管电磁系统计算方法的探讨
传统文献没有螺管电磁系统磁路计算公式,只有一些未经磁路计算,直接估算电磁吸力的计算公式,我们要创建一套直流螺管电磁系统的计算方法。
3.1 等值磁路图的构成和磁路计算公式
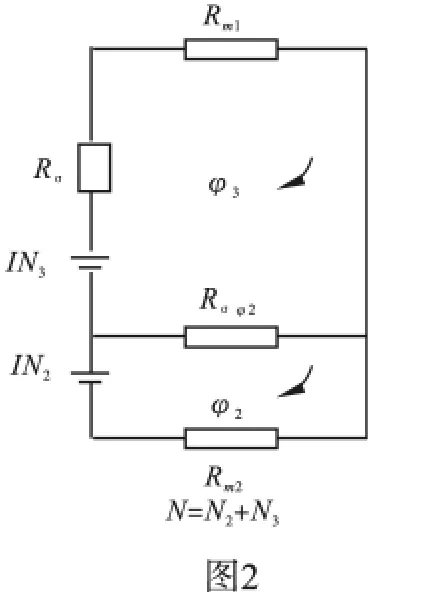
我们参考双E型电磁系统的办法,将整个线圈的集中磁势分为几段。CD-10直流螺管电磁系统没有静铁心段,只有动铁心段和气隙段。它们的匝数分别为N1、N2、N3,而N1=0,故总匝数N=N2+N3。集中磁势IN分为动铁心段IN2、气隙段IN3,便可将电磁系统所有部件的磁阻Rm绘成详细的等值磁路图,甚至包括两导磁部件接缝处的非工作气隙的磁阻。再将详细的等值磁路图化简,即串联的磁阻用一个标号,获得CD-10直流螺管电磁系统简化的等值磁路图,如图2所示。图2是将线圈磁势分为二段的等值磁路图。根据等值磁路图2,用回路法可推导求出气隙磁通φ3和动铁心磁通φ3的计算公式。
也可借式(1)求得气隙磁通φ3,即将交流后磁阻抗Zm换为直流磁阻Rm,此时N1=0,Rσφ1=0代入式(1),则直流螺管电磁系统气隙磁通:

式(2)将分段磁势IN2、IN3的电磁系统转变为集中磁势IN的形式,但还有分段磁势的影子。
用回路法求φ2,
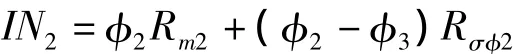
即

根据式(2)、(3)可求得气隙磁通φ3和动铁心磁通φ2。
将磁势分为二段,才能获得这样的成果。
3.2 气隙磁导计算
螺管电磁系统的主气隙,被线圈罩住,用分割磁场法计算它的气隙磁导。主要问题是如何确定它的边缘气隙磁导问题。气隙磁场受线圈磁势的约束,集中在主气隙,主气隙磁通扩散范围不应超出线圈铜线内腔。也就是说,它的边缘磁导被限制在线圈铜线内腔范围。这种处理的办法是按螺管电磁系统的边缘磁通适度减少,让中间部分磁通占的比例适度增大,从而保证长行程螺管电磁系统的电磁吸力增大,发挥螺管的优势。17个气隙位置的电磁吸力,计算值与实验值基本吻合。这种确定边缘磁导的方法,很符合实际。
笔者通过实践的探索,对自由空间边缘磁导m值的扩散宽度(不被线圈罩住的气隙为自由空间)定出取舍的规律,很符合实际,并用公式概括用分割磁场法计算气隙磁导。计算气隙磁导既方便又准确[2]。
3.3 磁路计算
CDS-10直流螺管电磁系统的磁路是非常饱和的,要凭公式(2)、(3)计算它的磁路,需要采用逐步渐法,逐步确定它的支路磁阻Rm1、Rm2。应当先从最大气隙位置80mm开始计算(即起动位置)。这个位置磁路饱和程度相对低些,进行零次计算。此时支路磁阻Rm1、Rm2由导磁体部件接缝处的非工作气隙的磁阻构成。代入式(2)、(3),计算零次气隙磁通φ3、动铁心磁通φ2。每次也求得支路磁阻Rm1、Rm2。当前后两次计算的磁通φ2、φ3,支路磁阻Rm1、Rm2都比较接近时,就是磁路计算的结果。实际上电磁系统起始位置磁路饱和程度不会很高,稍算几次,便能获得所求结果。
再算气隙稍小位置75mm的磁路。75mm气隙位置的支路磁阻Rm1、Rm2,一定比80mm气隙位置的支路磁阻稍大一些。故可用80mm气隙位置的支路磁阻开始75mm位置的磁路计算。计算几次,便能获得满意的结果。
以较大气隙位置的支路磁阻作为基础,计算稍小气隙位置的磁路,能获得满意的结果。但气隙愈接近动铁心闭合位置,磁路饱和程度愈高,最后甚至要设法延长磁化曲线。每个气隙位置磁路计算反复计算的次数也会更多。
计算这种饱和磁路是一个比较艰巨的工作,后来开辟了BASIC语言程序、Fortran语言程序,用拉格朗日三点插值公式计算饱和磁路,取得很好的结果。
磁路计算的结果获得各个气隙位置的气隙磁通φ3、动铁心磁通φ2、漏磁通φσ=φ2-φ3,支路磁阻Rm1、Rm2。为螺管电磁系统的电磁吸力计算打下良好的基础。
3.4 电磁吸力计算
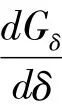



螺管电磁系统的电磁吸力:

传统文献常用下式直接估算螺管电磁系统的电磁吸力:
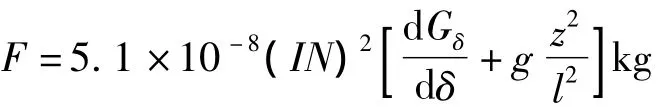
前一项为端头力,后一项为螺管力。
没有计算磁路,找不出气隙磁压降Uδ,只好用线圈的总磁势IN估算,当然不适用于实际。
4 分段磁势电磁系统
在2.3节已经阐明对双E型、螺管型电磁系统,可以打破传统将磁势分为几段,构成详细的等值磁路图,再化简,获得具有分段磁势的简化等值磁路图。然后再用电路的回路法,求解气隙磁通φ3,可得到一个从未见到过的磁路计算气隙磁道的公式。这个新公式又把分段磁势的电磁系统转化为集中磁势的电磁系统。转化的办法就是对集中磁势IN,乘一个磁势转化系数K。分段磁势电磁系统是为了解决衔铁插入线圈内部电磁系统的计算问题,人为地制造出来的。
转化系数K,笔者以前称它为磁势修正系数,现在看来又要将它改称为转化系数。它是将分段磁势电磁系统转化为集中磁势电磁系统的转化系数。
用线圈集中磁势计算磁路是磁路计算中的传统。
5 电磁系统的物理数学模型
由分段磁势电磁系统推导出来的磁路计算公式,也可适用于外衔铁电磁系统。
由双E型分段磁势电磁系统推导出来的气隙磁通的计算公式,按条件改造,也可适用于单E型电磁系统。单E型电磁系统为外衔铁电磁系统,按分段磁势的观点,它们的动铁段线圈匝数N2、气隙段线圈匝数N3均为零,它们静铁心段线圈匝数N1等于线圈的全部匝数N,即:

而且它们的归化漏阻Rσφ2=0,将这些数据代入式(1),则得单E型电磁系统气隙磁通φ3的计算公式为
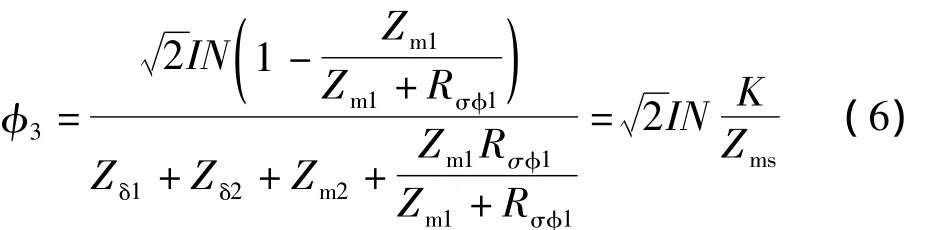
所以用分段磁势电磁系统推导出来的磁路计算公式,也可改造成为外衔铁电磁系统的磁路计算公式。这个绕弯子的办法建立起来的计算公式。这个公式,可适用内、外衔铁电磁系统,即可推广适用于双E、双U、螺管、单E、单U、拍合等形式电磁系统,成为内、外衔铁电磁系统的物理数学模型。
6 结论
(1)对内衔铁电磁系统(即衔铁插入线圈内部的电磁系统),如螺管、双E、双U型电磁系统,可以将它们线圈的磁势先分段,构成等值磁路图,再从理论上设法变成集中磁势,绕一个弯子,才能顺利进行磁路计算。双E型、螺管型电磁系统都是运用先分段再集中的概念,计算磁路的实际例子。
运用将线圈磁势分段的办法,解决了螺管电磁系统磁路计算问题。
(2)对外衔铁电磁系统,如单E、单U、拍合等型式的电磁系统,也可运用分段磁势电磁系统转化而来的公式进行磁路计算。
(3)计算螺管电磁系统的气隙磁导时,最好把边缘气隙磁导扩散的范围,限制在线圈铜线内腔范围之内。

[1]左全璋.交流电磁系统的一种计算方法[J].低压电器,1973.4.
[2]左全璋.如何比较准确地运用分割磁场法计算气隙磁导[J].防爆电器,1988.5.
[3]左全璋.直流螺管电磁系统静特性计算和实验[J].低压电器,1976.4.
[4]左全璋.交、直流长期带电电磁阀的研制[J].电气开关,1995.4.
[5]左全璋,李贤柱,殷世雄.自锁电磁阀电磁系统的计算方法[J].防爆电器,1983.3.
[6]左全璋,吴耀安,等.电磁铁的效率和输出[J].电器技术,1982.1.
[7]左全璋.磁路计算中的一些新概念[J].防爆电器,1987.1.
