一种基于序列图像的交互式快速三维重建方法
2012-07-25张树生白晓亮
李 亮,张树生,白晓亮,贺 强
(西北工业大学现代设计与集成制造技术教育部重点实验室,西安710072)
1 引言
三维模型具有更加丰富的视觉效果,因而越来越受到人们的青睐。尽管利用三维建模软件(3D Max、Maya等)或三维光学扫描设备获得三维模型越来越容易,但是这类获取通常是一项繁琐且代价高昂的工作。基于图像的三维重建具有成本低,简便等优点,因此成为了计算机图形学和计算机视觉领域当前的研究热点。
与基于图像的自动三维重建相比,交互式三维重建具有更高的可靠性和准确性[1]。因此,交互式的三维重建方法得到了深入研究,出现了相对成熟的商业软件系统,如Photo-Modeler、insight3D等。然而现有的交互式重建方法的建模过程较为繁琐,且交互工作量较大。该类方法通常的建模流程是:首先在多幅图像间手动构建匹配点对,然后连接这些点形成反映物体结构信息的多边形,最后计算各个匹配点的三维坐标,从而得到三维模型。因此,如何使交互建模过程更加简捷、高效且尽可能减少交互的工作量是当前交互式三维重建的目标。
综上所述,提出一种快速、基于序列图像的交互式三维重建方法。通过在序列图像上交互选取少量的点即可构成反映物体轮廓特征的多边形,根据该多边形,自动提取出物体精确的外形轮廓,通过轮廓点匹配的方式重建出三维模型。该方法无需精确指定匹配的点对,显著降低了交互工作量。
2 图像及摄像机参数获取
数码相机作为一种普通的家用电器已经普遍存在于人们的日常生活中。采用普通数码相机以定焦方式获得序列图像。从不同角度,拍摄不少于3幅的物体图像,按照角度的大小顺序组成序列图像。
摄像机参数的获取采用计算机视觉中成熟的SFM[2](structure from motion)技术,SFM 技术提供了一个很好的摄像机参数获取方案,其能够从序列图像得到摄像机的内外部参数,以及一些用来进行摄像机定标的匹配点对。
3 轮廓的半自动获取
物体的轮廓反映了物体的尺寸及形状信息。通过交互与轮廓自动跟踪结合的方式来获取物体的轮廓,这样既保证了轮廓提取的准确性,也减少了用户的工作量。用户首先在图像上拾取点,然后连接点以构建一个逼近物体轮廓形状的多边形。在此基础上,利用轮廓跟踪算法自动提取出多边形每条边对应的轮廓。
3.1 轮廓的自动跟踪
首先对图像进行超级像素[3]的分割,然后在超级像素分割结果的基础上,采用迪杰斯特拉最短路径算法[4]自动跟踪轮廓。
将图像划分成一个个具有相同颜色属性的小区域,称这样的区域为超级像素,如图1所示。超级像素之间的边界很好地反映了物体的轮廓,因而利用超级像素之间的边界来提取轮廓可极大提高轮廓跟踪的效率。

图1 超级像素分割结果
对图像进行超级像素分割后,在交互建立的轮廓多边形基础上,利用最短路径算法来提取相应的轮廓。寻找轮廓多边形其中一条边所对应的准确轮廓的具体过程如下:
Step1根据轮廓多边形的一条边,自动扩展出一个矩形区域,将这个区域内超级像素的边界点加入到顶点集V中,作为图G的顶点,将距离这条边其中一个端点最近的一个超级像素边界点作为最短路径的起始点v0。
Step2计算V中任意两点vi,vj之间的代价值。首先利用vi,vj的图像坐标计算它们之间的欧氏距离:
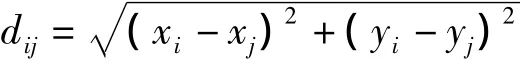
若dij<1.5,即两点相邻,则这两点之间的代价值为Gij=dij/m;若 dij>1.5,则代价值为 Gij=max=1000。m为点vi,vj所在边界两边的两个超级像素的颜色直方图比较结果,m越大两个超级像素的颜色差异越大。
Step3将v0加入到集合S中,初始化disti=G0i,将v0到其余顶点的路径长度初始化为代价值。
Step4从图 G中选择顶点 vk,使得 distk=min(disti|vi∈V-S),则vk为目前求得的下一条从v0出发的最短路径的终点。
Step5修改从v0出发到集合V-S上任一顶点vi的最短路径的长度。如果
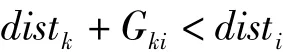
则
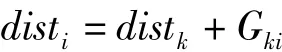
Step6重复步骤Step4、Step5,即可按最短路径长度的递增顺序,逐个求出v0到图中其它逐个顶点的最短路径,直到找到图G中每个顶点的最短路径。然后在图G中找到与该边另一端点距离最近的点,即可得到准确的轮廓。
3.2 轮廓逼近
由于成像和噪声等因素的影响,提取出的轮廓点所对应的三维点并不都是在其所属的直线或是曲线上。这会造成重建的三维对象不够准确且视觉效果差。一般的处理方法是对重建的三维对象进行光顺的平滑处理。虽然这样的处理也能得到较为真实的物体外形数据,但会显著增加后续的工作量。针对这一问题,在轮廓匹配和三维重建之前对轮廓点集进行逼近其真实形状的处理(见图2)。采用二分法对轮廓点集进行轮廓逼近,具体流程如下:
Step1将连接轮廓的起点和终点的直线作为初始直线。
Step2计算轮廓上从起点到终点的每一点到所对应直线段的距离。
Step3找出距离最远的点,如果距离大于所设定的逼近精度,则将该点所对应的直线段打断,分别以该点作为终点和起点,插入两条新的直线段。
Step4重复步骤Step2和Step3,直到最短距离小于设定的逼近精度。
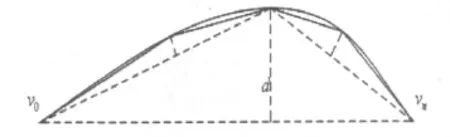
图2 轮廓逼近
4 轮廓点匹配
经过上述处理后,得到了真实的轮廓点集。对轮廓点集匹配后就能重建出对应的三维模型。
4.1 特征点的描述
在进行轮廓特征点的匹配时,需要为点建立一个描述子,描述子的优劣直接影响匹配结果。Transformed color SIFT[5]描述子具有旋转、尺度不变性,且能描述彩色图像,因此采用该描述子描述轮廓特征点。Transformed color SIFT消除了光强度变化引起的不规则颜色分布,抑制了直方图产生的偏移。该方法首先在RGB模型中对每个颜色通道减掉其颜色分布的均值μ,除以该通道下颜色分布的标准偏差σ,如下式所示
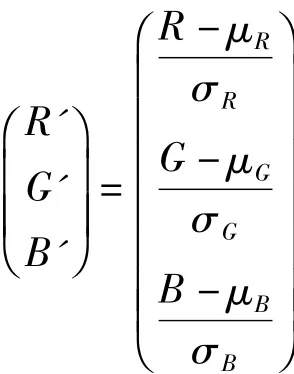
对原图像进行上述处理后,计算每个通道分量的SIFT[6]描述子,对每个轮廓特征点用128×3维的特征描述子进行描述,详见文献[5]。
4.2 轮廓点的匹配
对于图像 Ik上的轮廓点集{vk1,vk2,vk3…},首先确定与Ik匹配的图像Im。对于轮廓点集{vk1,vk2,vk3…}的点vki,用下述方法找到其在Im上的匹配点。
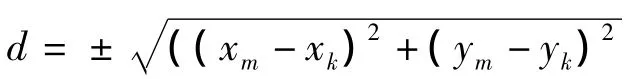
(2)对于轮廓点集中的点vki,按照上述方法找到其待匹配点集{vmi},用描述子描述vki及待匹配点集{vmi}中的点。
(3)计算点vki与其待匹配点集{vmi}中每一点的描述子向量的距离,距离最近的点为vki在图像Im上的匹配点。
5 三维重建
在进行了点的匹配后,就可以通过匹配点对得到三维点的坐标。对于一对匹配点对m1=(u1v11)T和m2=(u2v21)T,由二维图像点与三维空间点之间的映射关系可以得到:
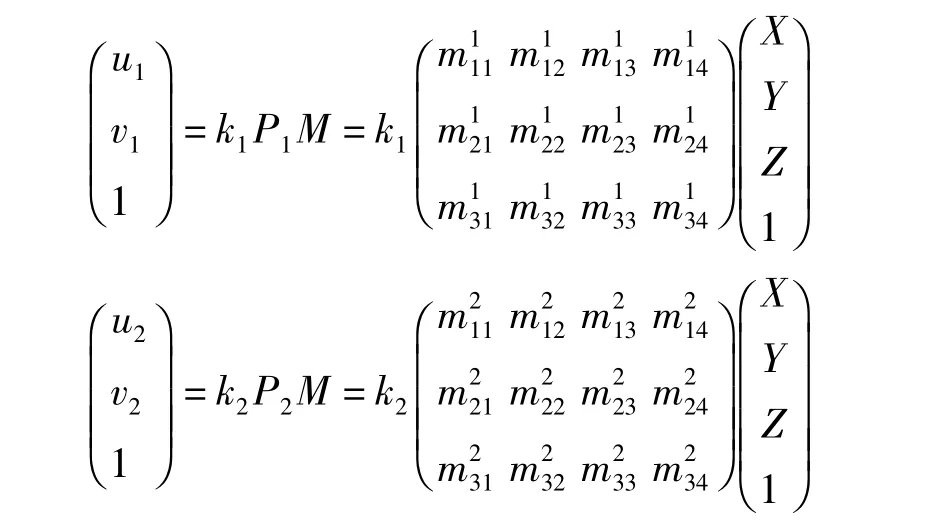
其中,M=(X Y Z 1)T为对应的空间点三维坐标,P1、P2为摄像机的参数矩阵。
利用上述两个方程,采用最小二乘法就可求出各点的 X,Y,Z 值[8]。
6 实验验证
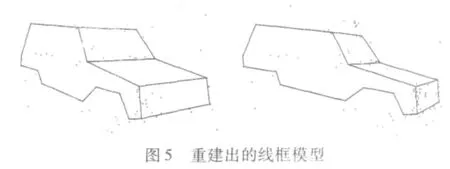
采用C++语言,在VS2010平台下开发了一个交互式快速三维重建原型系统,验证了所提方法的有效性。图3是采用普通数码相机拍摄的4副图像,图4为交互选取多边形的示意图,图5为三维重建得到的线框模型,图6为添加纹理效果的三维模型。

图3 序列图像


7 结束语
提出了一种快速、基于序列图像的交互式三维重建方法。利用普通数码相机所拍摄的相片,采用人工交互和轮廓自动跟踪的方式获得物体的轮廓,然后自动匹配出对应的点对,从而重建出了三维模型。该方法在一定程度上提高了交互式序列图像三维重建方法的自动化程度,获得了更为精确的物体轮廓,从而重建出更加逼近物体真实外形的三维模型。该方法对不含复杂曲面的物体重建效果较好,下一步的工作是增加对该类对象重建的处理方法。
[1] 史利民,郭复胜,高伟,等.基于语义交互的三维重建[J].计算机辅助设计与图形学报,2011,23(5):839-848.
[2] M Pollefeys,L Van Gool,M Vergauwen,et al.Visual modeling with a hand-held camera[J].International Journal of Computer Vision,2004,59(3):207-232.
[3] X Ren,J Malik.Learning a classification model for segmentation[C].In Proc.9th Int.Conf.Computer Vision,2003(1):10-17.
[4] 耿国华.数据结构[M].西安:西安电子科技大学出版社,2002:183-185.
[5] Koen E.A.van de Sande,Theo Gevers,Cees G.M.Snoek.Evaluating color descriptors for object and scene recognition[J].IEEE Transactions on PAMI,2010,32(9):1582-1596.
[6] David G L.Distinctive image features from scale-invariant key-points[J].International Journal of Computer Vision,2004,60(2):91-110.
[7] 吴福朝.计算机视觉中的数学方法[M].北京:科学出版社,2008:63-65
[8] 陈胜勇,刘胜.基于OpenCV的计算机视觉技术实现[M].北京:科学出版社,2008:400-401.
