一种改进粒子群算法在参数辨识中的应用

程 勇

(西安科技大学，西安710054)

1 引言

1995年Eberhart和kennedy提出了粒子群优化算法(Particle Swarm Optimization，PSO)，通过种群粒子间的配合和竞争达到群体指导搜索目标［1］。该虽然算法简单、易实现。但是，仍然存在着收敛速度慢等缺点。因此，很多学者针对这一研究热点提出了改进算法［2-3］。提出一种随机粒子群优化算法—DPRPSO。结果验证了DPRPSO算法不易陷入局部最小点和收敛速度快的特性。

2 随机粒子群搜索算法

2.1 标准粒子群算法

标准PSO算法首先初始化一群随机粒子(particle)，假设在D维搜索空间中，有m个粒子组成一群体，第 i个粒子在 D维空间中的位置表示为xi=(xi1，xi2，...，xiD)，第 i个粒子经历过的最好位置(有最好适应度)记为 pi=(pi1，pi2，...，piD)，每个粒子的飞行速度为vi=(vi1，vi2，...，viD)。在整个群体中，所有粒子经历过的最好位置为 pg=(pg1，pg2，...，pgD)，每一代粒子根据下面公式更新自己的速度和位置:

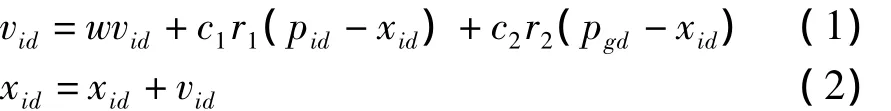
其中，w是惯性权重;c1和c2是学习因子;r1和r2是［0，1］之间的随机数。公式分别说明了，第一部分粒子先前的速度，即粒子目前的状态;第二部分认知部分，即从当前点指向此粒子自身最好点的一个矢量，反映了粒子的动作来源于自身经验的部分;第三部分为社会部分(Social Modal)，是一个从当前点指向种群最好点的一个矢量，反映了粒子间的协同合作和知识共享。

2.2 两群并列随机粒子群优化算法

结合标准粒子群算法的特点本文提出了一种两群并列随机粒子群算法。

2.2.1 随机搜索

随机搜索算法最显著的特点在于其算法本身的简单性，非常容易进行编程运算，以应用于特定的函数优化问题求解，而且基本上可以不需要预先设定的算法控制参数。

2.2.2 算法介绍

随机粒子群算法如下:

(1)将粒子群平均分成两群A、B。

(2)按照(3)混沌初始化 A、B粒子群(共 n个)，并且从中选出，适应度高的n个粒子。

Logistic映射如下:

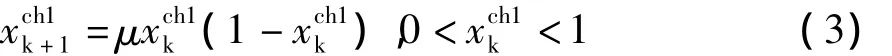
(3)找出全局最优粒子。

(4)进行PSO全局搜索，然后进行最优粒子半径r范围内的随机搜索，如果发现更好的粒子位置就要更新A、B两群中的最优粒子位置。

同时计算最优粒子的连续p次适应度的变化值，如果小于Δ，而且仍然没有达到目标误差，有可能已经陷入了局部最小值。这时，需要把最优粒子的位置在范围r内，利用随机算法优化，帮助最优粒子跳出局部最优值。这时的r表示随机搜索的半径，开始应该取的较小，当跳出局部最优值失败时，就需要扩大随机搜索的半径。

(5)对适应度差的最后m个粒子进行原位置上的混沌迭代，更新其位置，提高它的适应度。

(6)达到条件，停止搜索。算法结果如图1所示。

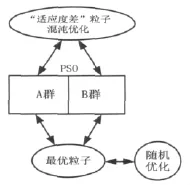
图1 算法结构图

3 算法验证

在参数辨识中以优化为基础的非线性系统参数辨识方法主要是寻找一组最优的参数向量，使预定的误差目标函数F(Z)值达到最小［5］。本文定义误差目标函数为输出误差的平方和，即:

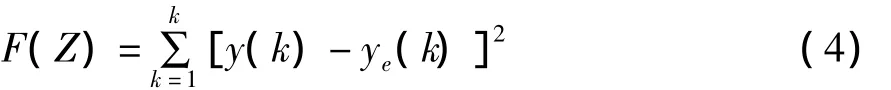
适应值是评定粒子优劣的标准，取式(4)的倒数作为适应度函数。设学习因子c1=1.4962;学习因子c2=1.4962;惯性权重w=0.7298;最大迭代次数MaxDT=1500;PSO粒子个数N=50;收敛误差终止条件enorm=10-6，RPSO算法中有5个随机搜索粒子。针对算法提出的算法特性，选取指数函数模型为辨识对象。

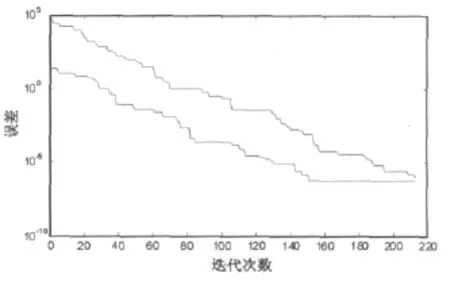
图2 标准PSO和RPSO算法误差收敛曲线

在y=aeb+cx中，原模型中 a=4.1240;b=2.1297，c=5.4900。x取值范围［-5，5］。需要辨识的参数是a，b，c。连续搜索100次，对结果进行统计:

PSO平均搜索229步，成功率74%，达到误差精度，停止搜索。a=4.113345480867251，b=2.109754600729356，c=5.510000331108581。

RPSO平均搜索153步，成功率95%，达到误差精度，停止搜索。a=4.123002142000102，b=2.120300570417860，c=5.489655809122442。

图2给出了搜索的平均结果，蓝色的曲线表示RPSO算法，绿色的曲线表示PSO算法。

可以看出，由于混沌算法的初始化，在辨识的开始阶段，DPRPSO就比PSO算法具有优势。随着算法的进一步展开，本文的算法在辨识过程中，利用两个并行的PSO集体，不仅提高了算法的效率，而且更加高效的利用了最优粒子的引导特性。因此，这个辨识过程具有更高的效率，更快的速度。

4 结束语

介绍了基于粒子群多样性和随机搜索所提出的一种改进型PSO算法DPRPSO。应用在参数辨识中，粒子群算法具有收敛速度快，辨识精度高的特点。最后辨识结果充分说明了DPRPSO是一种有效的PSO改进算法，也证明了该算法的有效性。

［1］ Kennedy J，Eberhart R.Particle swarm optimization［C］.Proc of IEEE Int Conf on Neural Networks.Perth，1995:1942-1948.

［2］ Kennedy J.Small worlds and mega-minds:Effects of neighborhood topology on particle swarm performance［C］.Washington DC:Proc of the Congress on Evolutionary Computation，1999:1931-1938.

［3］ 陈贵敏，贾建援，韩琪.粒子群优化算法的惯性权值递减策略研究［J］.西安交通大学学报，2006，40(1):53-56.

［4］ Mendes R，Kennedy J，Neves J.The fully informed particle swarm:Simpler，maybe better［J］.IEEE Trans on Evolutionary Computation，2004(8):204-210.

［5］ 冯培悌.系统辨识［M］.杭州:浙江大学出版社，1999.