单调递减序列的离散变换及其灰色建模

孔新海，刘志斌，魏 勇

0 引言

灰色系统理论自诞生以来,已在许多领域得到了广泛的应用,特别是在社会、经济预测等方面应用更为广泛。作为灰色系统理论重要内容之一的GM(1,1)模型,其应用价值在越来越多的领域中得到体现。从GM(1,1)模型建模机理来看,对递增离散点列x(0)，其一次累加生成序列x(1)是单调递增的，我们常直接建模即可；对递减离散点列x(0)，由于其一次累加序列x(1)也是单调递增的，其模拟值也是递增的，如果对进行累减还原，常常被认为会产生不合理的计算误差，因此很多学者通过各种变换，如：反向累加生成、倒数变换、线性变换，把递减序列变换成递增序列，再建立GM(1,1)模型。其实，递减序列也可以建立GM(1,1)模型，有时建模效果还非常好。本文在文献[1][2]的基础上，提出一种基于单调递减序列的离散变换，以期提高序列的光滑度。

1 基本概念

定义 1设序列 X={x(1),x(2),…,x(n)}，称 σx(k)=为序列X的级比；称δx(k)=|1-σx(k)|为序列X的级比偏差；称为序列X的光滑度。定义2若为两单调递减序列,且对∀k=2,3,…,n,有 ρa(k)＜ ρb(k),则称序列更光滑。

定理1对于单调递减序列 x(k)＞0,非负变换y(k)=F(x(k))满足不等式 ρx(k)＜ρy(k)的充要条件为F(x(k))可以表示为 F(x(k))=x(k)f(k)，其中序列 f(k)非负，且严格单调上升。

证明：先证充分性。由于x(k)、f(k)非负，且 f(k)严格单调上升，则对i=1,2,…,k-1，有

x(k)x(i)f(i)＜x(k)f(k)x(i)

两边对i求和，可得

即

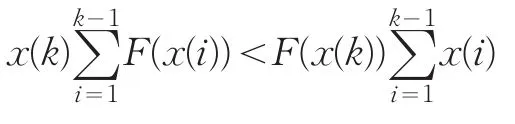
从而

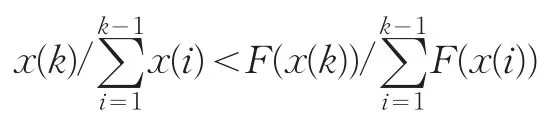
再证必要性。由

取k=2，得

x(2)/x(1)＜F(x(2))/F(x(1))

即有

F(x(1))/x(1)＜F(x(2))/x(2)

令 z(k)=x(k+1)，则

F(z(1))/z(1)＜F(z(2))/z(2)

显然有

F(x(2))/x(2)＜F(x(3))/x(3)

2 基于单调递减序列的离散变换

2.1 离散变换

定义3对于单调递减的原始序列X={x(1),x(2),…,x(n)}，进行离散变换y(k)=F(x(k))。

(1)若X为减速下降，即σx(1)＞σx(2)＞…＞σx(n-1)＞1，则变换算式为,d＞1,0＜s＜1。

(3)若X为加速下降，即1＜σx(1)＜σx(2)＜…＜σx(n-1)，则变换算式为：

令 φ(k)=(k+1)s-ks，当 σx(k)递减，则 φ(k)也要递减，即0＜s＜1；当σx(k)递增，则φ(k)也要递增，即 s＞1。

令 ϕ(s)=(k+1)s-ks,则 d(k+1)s-ks=dϕ(s),所以 d 与 s的增减具有反向性。若d放大，s缩小；若d缩小，s放大。

性质(1)为了保持变换序列与原始序列单调性一致，当 X为单调递减序列时，对任意的k，d和 s满足d(k+1)s-ks≤σx(k)；(2)该变换能够缩小级比偏差；(3)该变换还原误差不变。

证明：(1)当 X为单调递减序列时，由于σy(k)=对 任 意 的 k,要 使y(k)≥ y(k+1),则,即 d(k+1)s-ks≤ σx(k)。

下面给出一种确定d和s的方法（级比偏差之和最小法）。

因为 σy(k)=σx(k)dks-(k+1)s，所以

δy(k)=|1-σy(k)|=|1-σx(k)dks-(k+1)s|

(1)d(k+1)s-ks≤σx(k)；(2)d＞1；(3)s的范围。

2.2 建立GM(1,1)模型

设X(0)={x(0)(1),x(0)(2),…,x(0)(n)}为单调递减的原始序列，分析其级比变化趋势，利用级比偏差之和最小确定d与 s，再进行数据变换 y(k)=x(k)dks，对变换序列Y(0)={y(0)(k)}建立GM(1,1)微分方程模型

其中：

求解上述微分方程的时间响应函数并离散化，则

还原得

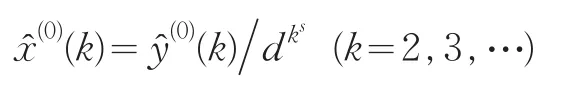
3 实例分析

例1[3]某10mg血药在相同时间间隔测得的浓度数据为

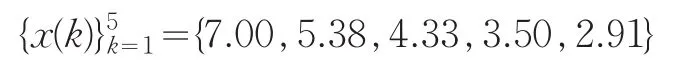
其级比序列为

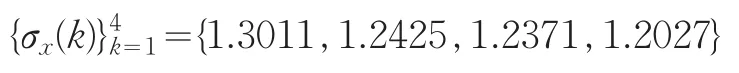
这显然是个增长速度减缓的序列。利用本文提出的离散变换y(k)=x(k)dks，d＞1,0＜s＜1，对原始数据进行离散变换处理，然后再建立GM(1,1)模型。根据级比偏差之和最小,可求得d=1.466919,s=0.7264035,建立GM(1,1)模型，模拟效果如表1所示。

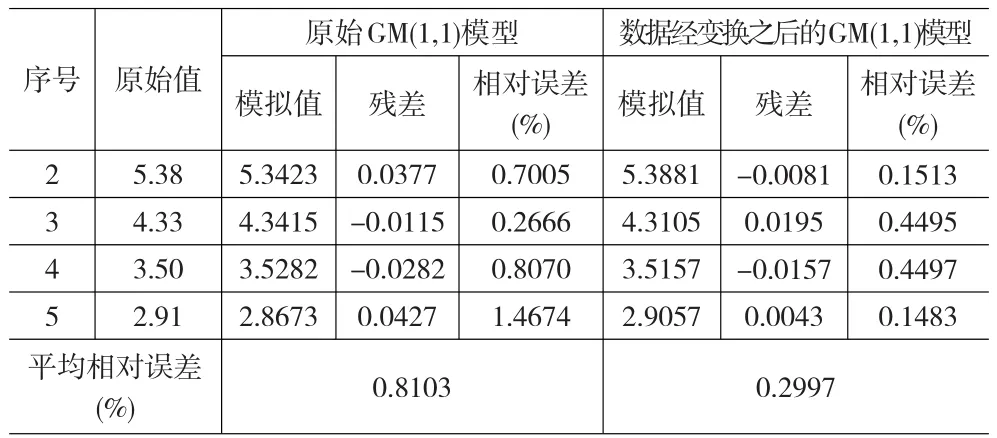
表1 模拟效果比较

从表1可以看出，经本文方法变换之后建立的GM(1,1)模型模拟效果比原始模型的结果要好。

例2[4]在N2O5的热分解反应过程中,在等时间间隔里实验测得N2O5的分压数据为X(0)={24.7,18.5,14.0,10.5,7.8,5.8,4.4,3.3},这里温度T=318.2K ，单位：cm Hg，其级比序列为={1.3351,1.3214,1.3333,1.3462,1.3448,1.3182,1.3333}，这是个相对平稳的序列。这里令s=1，取，建立GM(1,1)模型，模拟效果如表2所示。

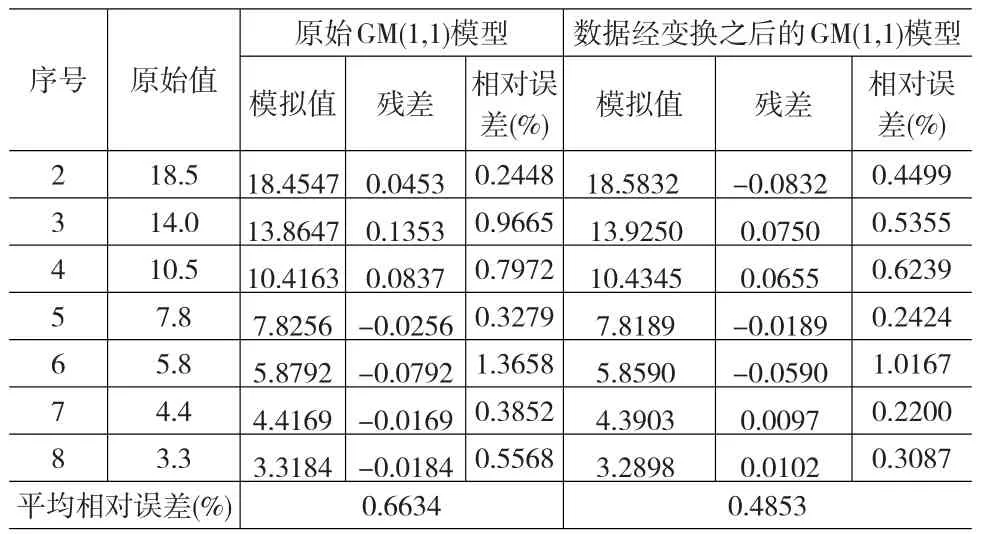
表2 模拟效果比较

例3[5]某油田在递减阶段的年产量为X ={14.38,14,13.06,12.09,10.98,9.88,8.27}，单位：107t/a,其级比序列为={1.0271,1.0720,1.0802,1.1011,1.1113,1.1947这是个级比增长的递减序列。利用本文提出的离散变换y(k)=x(k)dks(d＞1,s＞1)，对原始数据进行离散处理，然后再建立GM(1,1)模型。根据级比偏差之和最小,可求得d=1.008491,s=2.057443,建立GM(1,1)模型，模拟效果如表3所示。

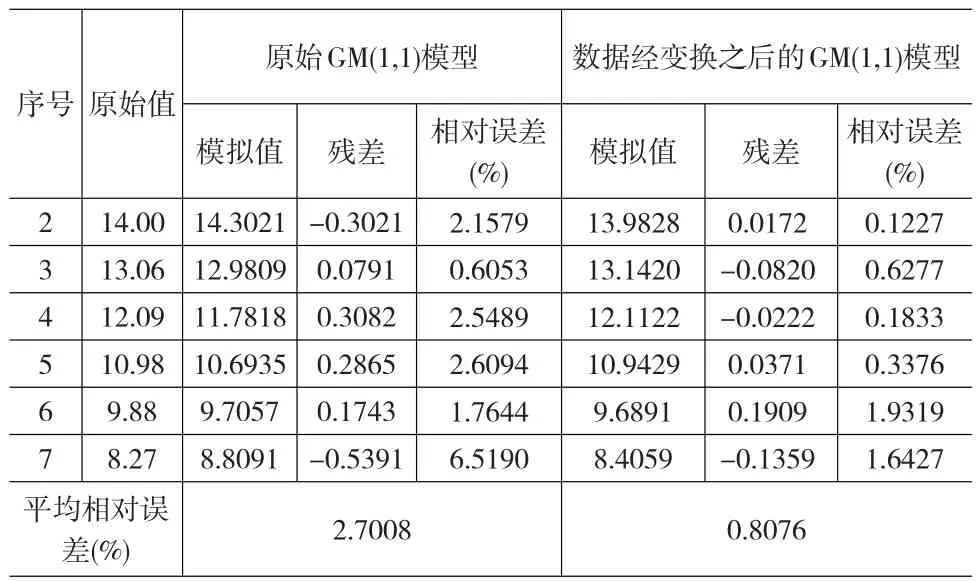
表3 模拟效果比较

4 结语

针对原始序列为单调递减的情况，本文提出了一种提高光滑度的离散变换，这种变换能更好地适应原始数据序列的变化趋势。根据原始序列的增长速率来调整离散变换算式的参数，以缩小原始数据序列的级比偏差，提高GM(1,1)建模精度。文中所举实例也说明了这种离散变换的可行性。本文只是针对原始序列为单调递减的情况进行了讨论，其他情况将在其后作进一步研究。

[1] 黄福勇.灰色系统建模的变换方法[J].系统工程理论与实践,1994,14(11).

[2] Yong Wei,Yi Zhang.An Essential Characteristic of the Discrete Function Transformation to Increase the Smooth Degree of Data[J].The Journal of Grey System(UK),2007,18(3).

[3] 杨保华,张忠泉.灰色GRM(1,1)药物动力学模型[J].数理医药学杂志,2003,16(1).

[4] 安燕,吴启勋.倒数累加生成灰色RGM(1,1)模型及其在化学动力学上的应用[J].计算机与应用化学,2006,23(2).

[5] 陈元千,郭二鹏.新型油田产量递减模型的建立与应用[J].中国海上油气,2008,20(6).