基于均匀设计的土地抽样调查研究

胡动刚，刘 忻，李春洋

0 引言

“均匀设计”是我国独创的有巨大应用潜力的科学统计方法[1]，经过近30年的实践检验和不断完善，在生产和科研等领域获得了广泛应用，产生了很大的经济、技术和社会效益。它的特点是所选择的实验点在实验范围内均匀分布，且实验点的数目远远小于其他的实验方法（如：正交设计），这正好符合土地调查中抽样方案设计的要求，能够在较少的抽样调查样本的情况下，获取比较准确的多指标信息结果，不仅避免了大量人力、物力和财力的消耗，而且也实现了土地资源信息的社会化服务，满足经济社会发展及国土资源管理的需要。

1.均匀设计理论

1.1 基本思想

均匀设计是中国科学院王元院士和香港浸会大学方开泰教授在1978年提出的。其基本思想是，在实验范围内选出有代表性的试验点，使其尽量多地携带实验信息。均匀设计运用数论方法使实验点在实验范围内“均匀分散”，而不考虑“整齐可比”（即：实验处理按水平数重复多次），故在保证实验准确反映实验内部规律的同时，使得实验次数比其他实验设计方法大大减少。因此，利用均匀设计的方法研究多指标土地抽样调查方案，以期用尽可能小的样本来相对高精度地估计总体多指标的数量特征。

1.2 均匀设计表的构造

均匀设计表是一个n行m列的矩阵，每一列是{1，2，…，n}的一个置换，表的第一行是{1，2，…，n}的子集，可以是真子集，记为Un（qt），其中U表示均匀设计,n表示试验次数,q表示每个因素的水平个数,t表示最大的独立因素个数。由此得出的均匀设计表数量太多，下面介绍用最好格子点法构造的均匀设计表[3]。

步骤1：确定第1行。实验次数n为奇数时，寻找比n小的且互素的所有正整数，构成第1行（h1，…，hm）。

步骤2：其余各行由第1行生成。表的第i行（i＜n）第j列的元素uij=ihj[mod n]，而unj=n。

步骤3：表Un*（qt）的生成。当n为偶数时，由n+1确定的表Un+1（qt）去掉最后一行得到。

1.3 均匀设计的特点

（1）每个因素的每个水平做一次且仅做一次实验。

（2）任两个因素的实验点描在平面的格子上,每行每列有且仅有一个实验点。

（3）每一个均匀设计表需要由统计学家编制的使用表配套使用。

（4）均匀设计在稳健回归模型而非方差分析模型下达到最优[4]。

2.多指标抽样调查

抽样调查是指从研究对象的总体中按照随机原则抽取一部分个体作为样本进行调查，并以对样本进行调查和统计的结果来推断总体，据此推断有关总体的数字特征一种非全面调查的统计方法。在实际抽样调查工作中，对所要研究的总体进行某一项指标进行调查，称之为单指标抽样调查，它在现实生活中比较少见；而更多的是多指标抽样调查，即在对某一研究总体进行抽样调查时，人们总是多个指标同时进行，从而同时可获得多个指标的样本数据，对总体进行统计分析[3]。

2.1 指标假设

在研究多指标抽样方案时，需要首先搞清楚指标属性是连续型还是离散型，对总体指标做出下面两点假设：

（1）n个指标x1，x2，…，xm相互独立。如果不独立，可以通过主成分变换的方法选择样本；

（2）n个指标x1，x2，…，xm均为定量变量。特别的，若部分为定性变量亦可。

为了方便起见，用矩阵形式表示总体容量为n，指标数为m的样本数据。

2.2 均匀化处理

值得注意的是，当抽样指标xj不满足均匀分布时，需要对密度函数f（xj；·）进行均匀化处理，将之等概率的q分位，分为区间分别为：

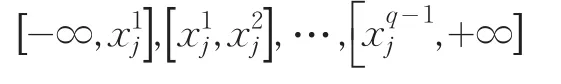
f（xj∣k，·）在水平k∈（1，q）下的概率密度为

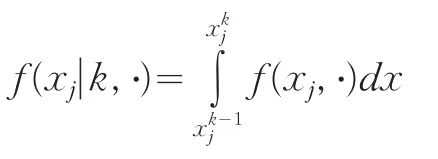
3 应用

3.1 抽样框的选取与建立

武汉城市圈，又称“1＋8”城市圈，是指以武汉市为圆心，包括黄石、鄂州、黄冈、孝感、咸宁、仙桃、天门、潜江周边8个城市所组成的城市圈，并以武汉市为城市圈中心城市，黄石市为城市圈副中心城市，其国土面积达58051.9平方公里，占湖北省的31.23%，承担着超过全省一半以上的人口和财政收入以及60%以上的经济总量和80%以上的对外贸易。因此，面对发展和建设必然要占用土地这一无可回避的现实，在武汉城市圈城市化进程中，有必要对其土地节约集约利用状况进行多指标抽样调查，为武汉城市圈“两型社会”建设提供持续有力的资源保障和优质高效的服务，实现武汉城市圈的可持续发展。

表1 武汉城市圈9市行政区划表

根据近几年的《湖北省统计年鉴》，本文选取了武汉城市圈9个市的总共47个区县为样本，建立抽样框（见表1），并可以依据各市的统计资料查阅相关指标值。

3.2 多指标抽样方案的设计

从土地节约集约利用的内涵入手，考虑调查过程中资料和数据搜集的可操作性，综合“经济-社会-生态”和“集约-高效-协调”等因素，参考《湖北省人民政府关于推进土地管理改革促进武汉城市圈“两型”社会建设的意见》，从武汉城市圈土地集约利用的强度、投入和效益等实际情况出发构建了下面的评价指标体系表[4]（见表2）。

表2 土地节约集约利用评价指标体系表

根据表1、表2，我们可以将多指标抽样调查问题转化为一个U9（312）的均匀设计问题。因此，我们通过U9（312）的均匀设计表得到关于武汉城市圈的土地节约集约利用的抽样调查方案，即抽样调查方案（见表3）。

表3 均匀设计表U9（312）

3.3 评价

不难发现，利用均匀设计表建立的多指标抽样调查实质上一种特殊的分层整群抽样调查，其优越性表现在以下几个方面：

（1）调查成本可控且较低。我们知道，样本容量直接与调查费用相关，容量越大，调查费用越高。用下面的线性函数表示调查成本

C=C0+cn

其中，C0是与样本容量n无关的固定成本，包括组织、宣传、抽样抠的准备等；而c是平均每抽一个单元的费用，包括调查本身的费用、旅费以及数据处理费等[10]。均匀设计理论告诉我们，对于同一个指标体系，可以选择抽样次数较少的不同的设计表，比如，上述的土地调查方案不仅可以选取U9（312），也可以选择U8（412），它们的区别在于要求的水平以及对应的实验次数和精度不同，使用者可以根据自己的需要来。但是，无论哪一种，其容量都不大，当然，调查成本是较低的。

（2）抽样调查的误差较小。利用U9（312）的均匀设计抽取12个单元，指标xi在水平q=3下的样本均值估计

每个水平q下的抽样比例为

在指标均匀化处理且相互独立的情况下，抽样误差完全来自于同一水平q下的不同单元随机抽样误差，即有指标xi的均值方差

进而有指标xi的均值估计总方差为

（3）进行适当的列变换可以达到更好的效果。比如，对调任意两列即变换指标次序不改变均匀设计表，那么，我们在抽样调查中，可以根据实际情况调整指标的先后顺序以降低难度和成本等；再如，选取第7和8列，可以得到“土地集约利用投入”的抽样结果，因此，选择其中适当的列能够考察对应的评价准则层的抽样结果。

[1] 王元.均匀设计—一种试验设计方法[J].科技导报,1994,(5).

[2] 方开泰，马长兴.正交与均匀试验设计[M].北京:科学出版社,2001.

[3] 马树才，韩云虹，陈谨玫.对多指标抽样调查及其统计推断进行[J].数据分析,2007,(4).

[4] 王业侨.节约和集约用地评价指标体系研究[J].中国土地科学,2006,(3).

[5] 冯士雍.抽样调查——理论、方法与实践[M].上海：上海科学技术出版社,1996.