和声搜索的半监督聚类研究与应用

王华秋

（重庆理工大学 计算机科学与工程学院，重庆400054）

0 引 言

由于计算资源有限，对于应用程序开发者而言，计算性能是一项关注点。开发者总是致力于如何写出高效的科学计算代码以最优地利用超级计算机或其它的计算资源，然而，他们常常由于缺乏一些必要的信息而无法让代码最优化，这些信息包括：体系结构、内存机制、处理器网格等。这些复杂而隐藏的因素决定了程序的性能，比如：内存使用、I/O、编译器、操作系统等等。

用于高性能计算机的性能分析工具就可以帮助使用者写出高效的代码。这些工具能够提供程序性能评测值，并能发现一些瓶颈。瓶颈是指在程序执行时，运行时间由于无效资源的占用而浪费掉了。只要识别出瓶颈，开发者就可以修改程序以提高运行效率。正如现如今有许多并行计算硬件和并行编程语言一样，性能分析工具也是层出不穷，其中有代表性的是如下几种：Paradyn，TAU，Periscope，Vampir，KOJAK，SCALASCA，mpiP。

聚类机制为这些工具提供了一种基本的多变量统计分析的方法，所有处理器的Performance和Region这两个属性对应的Serverity值被提取出来，组成一个由处理器个数为行，Serverity为列的高维矩阵。我们用聚类算法对这些处理器进行分类，以检测每一类处理器在不同代码区域出现性能瓶颈的概率分布，以便对每一类处理器进行合理的资源调度。用于GENE代码分析的处理器有1024个，这些处理器产生的性能瓶颈维度有39列之多，这样会产生1024＊39的矩阵，如何评价这些处理器的性能，因此对这样的性能矩阵进行划分，使其产生少数具有相似性能的处理器集合将是非常有意义的，聚类后的处理器将有利于发现隐藏在巨大数据集后的并行系统整体运行趋势。

如今，存在着诸如划分、层次、密度、网格等聚类算法。划分聚类是最常用的一种方法，也是许多启发式搜索算法首选的优化目标，这些启发式搜索算法已广泛地用于聚类中心的发现中，这些算法能在问题域内找到所有可能解，而且能避免陷入局部最优解。这些算法例如克隆选择［1］、蚁群 优 化［2］和 粒 子 群 优 化［3］。和 声 算 法 是 Geem 在2001年提出一种由音乐灵感激发的优化算法［4］，受到广泛关注，和声搜索算法已经用于许多工程和科学领域，比如：图像分割［5］、Web文本聚类［6］、水处理［7］。因此本文也用和声搜索算法实现了快速准确地聚类，无论数据分布如何、形状如何、大小如何，性能好的搜索划分算法都可以对其聚类。

众所周知，每个都数据包含一定数量的维度 （或者称为属性），聚类算法就是将这些多维数据进行划分，在划分之前并不知道需要划分成为几部分，只是将每一类内部变量尽量聚集在一起，而类与类之间的距离尽量远离，两点之间的差异用相似度或者距离计算。聚类的这种不确定性正是在于聚类学习是无监督的过程。

基本的划分算法认为所有的维对于聚类同等重要，事实上，一些维存在冗余、无关、甚至易产生误导的异常点。因此特征选择技术出现了，这是一种用于高维数据聚类的最佳特征子集选择技术［8］。

特征选择不仅提高了聚类的性能，而且对于简化了聚类模型。特征选择一般是在聚类之前完成的过程，但是也有一些算法将其集成于聚类算法中，即在聚类的同时进行特征选择，文献 ［8－9］就是将特征选择和EM聚类结合在一起，在其影响下，文献 ［10］提出了一种利用和声搜索算法的聚类和特征选择同步进行的方法，该方法将特征选择作为和声搜索聚类过程的一部分，每次搜索的目标不仅包括聚类中心，还包括被选择出来的属性 （维），而且为了获得最佳的聚类中心数量，每次搜索需要不断改变聚类的中心数量。这种集成模式的搜索采用的评价函数则是聚类误差和属性 （维）相对中心的偏差两部分之和。这些改进的确提高了划分聚类的性能，但是同时带来了一些问题：①算法复杂度较高，随机的聚类中心和随机的特征属性的组合将是非常庞大的，这对于高维度大数据而言，其算法复杂度是可想而知的；②性能评价函数不太合理，将聚类误差和属性偏差结合在一起不利于评价总误差究竟是由于聚类中心数量不适当而带来的误差，还是由于属性特征选择不合理而带来的偏差，从而造成每次迭代无法正确调整3个目标值：聚类中心数、聚类中心、属性维度。这将对算法的准确度产生不可忽视的影响。

以上的做法是对高维数据的属性 （特征）进行选择，没有被选上的属性将被忽略或删除，进一步，有的学者提出属性加权的思想对特征选择进行泛化，即是为每一维设置一个0到1之间的权值，而不是直接保留或删除某些属性 （维）。换句话说，如果某一属性的特征比较明显，那么它的权值就较高，从而对聚类结果的影响就较大；反之，特征不显著，则权值较小，而影响较小。这样看来，特征选择就是为每一维设置合理的权值。近年来，许多学者致力于研究这种特征加权的方法以提高聚类质量。

Huang［11］提出了一种用于Kmeans的特征属性自动加权的机制，他们利用迭代公式不断修正权值，而Kmeans算法的有效性并没有被影响，然而，该方法需要使用者主观指定一些参数值，而且，该方法获得的权值无法显著区分属性是否具有代表性和不相关性。

文献 ［12］提出了用优化的方法对属性进行加权，首先测量不同特征属性的分散度，然后构造了凸Kmeans算法以决定最优权值，同时保证簇内部平均分散度最小以及簇之间的平均分散度最大，在实践中，对于所有属性进行加权并不适合高维数据聚类。文献 ［13］提出了COSA方法用于对子属性进行层次聚类。但是求解这个优化函数需要面临巨大的算法复杂度。受到这样的启发，一些学者将这种特征加权的优化方法用于子空间聚类［14－15］。

根据以往研究的经验，结合需要解决的问题，本文提出了一种采用了和声搜索的半监督聚类算法，该算法克服了文献 ［10］提出的算法的那两点问题，而且采用了一种简单可行的特征属性加权的方法是区别各个维在聚类中的不同作用，而不是忽略某些属性维，采用评价函数对不同的聚类中心个数进行评价，从而保证算法收敛时能够得到最佳聚类中心。最后本文将这种算法用于解决并行计算中的处理器聚类问题。

1 算法设计

按照引言的论述，我们要解决的问题有三点：①特征属性的加权，即数据维加权；②采用和声搜索进行数据聚类；③选择最优的聚类中心数。因此我们把算法分为三步完成：

（1）在聚类之前先进行特征属性的加权。

任何一维的数据如果过于集中，数据之间失去的区别，就不利于聚类了，这样的维所代表的属性就应该具有较小的权值；反之，如果这一维数据比较散乱，数据之间便于区分，那么这一维对聚类结果影响较大，应该分配较大的权值。本文就是按照这样的思路对每一维属性进行加权

这样wi就代表了第i维对于聚类的权值，这里stdi是第i维数据的标准偏差，meani是第i维数据的平均值，stdi标准偏差代表了每一维的变化性，用标准偏差除以平均值则可以将每一维的数据分散性归一化，使得所有维之间的权值具有可比性。

（2）利用和声搜索算法计算聚类中心。

聚类评价函数值作为和声算法的适应度，并采用一种新的调音概率公式改进和声算法，不断调整和声库直到算法收敛，直至聚类评价函数值的改变量小于要求或者达到迭代次数。

（3）选择最优的聚类中心数。

不断改变聚类中心数，利用第二步计算其聚类中心和评价函数值，选择评价函数值最小对应的聚类中心作为最后的输出。

由此可以看出，第二步事实上是本算法的关键，下面我们详细介绍这一步计算过程。

2 和声搜索聚类算法研究

和Kmeans、Kmediods、FCM等算法一样，和声搜索聚类算法同样离不开聚类中心反复 “迭代”，只不过这时的“迭代”演变成了 “演奏”。

2.1 初始化和设置参数

现已知样本

式中：n——样本数量，d——样本的维度，每一维数据的上界 Uxj∈d和下界 Lxj∈d。

（1）数据归一化：由于各维数据代表的意义不同，造成量纲不统一，这样不利于计算彼此的距离。由于在属性加权时我们

已经对每一维的数据计算了标准差和平均值了，这里就采用Z－Score归一化方法，由下式计算

（2）聚类需要确定的参数是：我们需要定义聚类质量评价函数，这个评价应该体现聚类的原则：簇内样本尽量靠近该簇中心，簇和另一个簇尽量远离。因此我们把尽量小的簇内距离除以尽量大的簇间距离作为评价函数 （也称为适应度）

式中：C——聚类中心的集合，k——聚类中心的个数，Ci和Cj分是第i个和第j个聚类中心，nj是属于第j类的样本数量。这样我们聚类的目标就是通过和声搜索到使得f（C，k）达到最小的C和k，C用向量的方式存储，C＝（C1，C2，…，Ck）＝ （c11，…，c1d，…，ck1，…，ckd），例如：第一个聚类中心就是c11，c12，…，c1d，第k个聚类中心就是ck1，ck2，…，ckd。

（3）和声搜索算法也有一些参数需要确定：和声存储库的行数 （HMS＝20），和声存储库的列数 （COL＝k＊d），和声存储库的选择概率 （HMCR＝0.9），调音概率（PAR＝0.25），随机带宽 （bw＝0.2），音演奏次数 （即迭代次数ITERATION＝100）或者停止条件 （适应度变化量小于一个小数DELTA＜0.01）。

2.2 初始化和声存储库

在这一步中，和声存储库HM矩阵最初由有上界Uxj∈d和下界 Lxj∈d限制的随机数组成

调用聚类质量评价函数计算各行和音的适应度，得到适应度列向量F＝ ［f1，f2，…，fHMS］T，记录其中最佳和最差的适应度及其对应的和声变量。

和声存储库的作用就是在每次迭代时，由此库产生出新的和声变量，并根据这新变量不断更新和声存储库，使之收敛到全局最优解。

2.3 演奏新的和音

一个新的和音向量

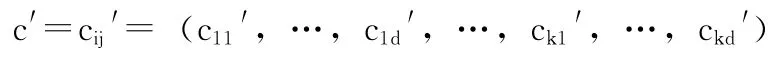
这里，1≤i≤k，1≤j≤d，这个新和音向量有3种途径产生：①和音存储库中选择；②从和音库中选择后调音；③在允许范围内随机产生。产生新的和音的过程称之为 “演奏”。

在第一种方法中，第一个类中心的第一维变量c′11将从和音存储库的第一列向量中随机选择，以此类推可以得到其它中心的各维变量cij’。

HMCR的变化范围是0到1，一般为0.6～0.9之间，本文为0.9，这是决定是否从和音存储库HM中选择性的变量的概率，换句话说，（1－HMCR）就是决定是否从上下限范围内随机产生新的变量的概率。选择操作如下

对于每一个从和声存储库中得到的变量还要决定是否调音，PAR就是初始调音的概率，一般为0.1～0.4之间，本文为0.25，概率 （1－PAR）就是不需要调音的概率。调音操作如下

所谓调音，就是在原来的变量的基础上增加或减少一个随机带宽量bw

上述3种方法产生的新的和音将被返回并用于更新和音存储库。

调音是避免和声算法出现 “早熟”的重要措施，在最初的和声算法中，并没有对调音概率PAR和随机带宽bw做调整，因此需要很多次迭代才能调出一个不同于其它的和声。当库中的和声趋同时，我们以一个远大于通常的调音概率PAR执行一次操作，同时增加随机带宽量bw，这样就能够随机产生新的音符，从而使整个和音库摆脱 “早熟”。

当和声库中的最佳适应度fbest与平均适应度favg满足如下关系

我们就认为和声库具有趋同的趋势，就适当提高调音概率PAR和随机带宽bw

这样的改进可以增加算法的随机搜索的几率，提高算法的全局收敛性，但是考虑到收敛时间会延长，因此PAR和bw的增加系数均不太大。

2.4 更新和音存储库

使用新和音向量c′＝cij′＝ （c11′，…，c1d′，…，ck1′，…，ckd′）作为聚类中心，调用聚类质量评价函数计算c′的适应度f′，如果新的和音向量c′在适应度上优于和音存储库中的最差的向量，那么和音存储库就需要更新了，新的和音向量将取代那个最差的向量。如果这个新的向量同时也是和音存储库中最优的，那么保存这个新向量的适应度为和音存储库的最佳适应度，这时的最佳适应度对应的变量就是最终聚集成为k个中心时的聚类结果。

2.5 检查终止条件

如果满足终止条件，结束聚类中心的搜索，否则，转到3.3节。终止条件就是：①迭代次数达到最大值；②评价函数值 （适应度）的变化量小于限定值。

3 算法复杂度分析

为了分析整个算法的复杂性，我们介绍一下整个算法的流程，如图1所示。

图1 算法流程

我们把整个算法分为了若干段，每一段完成一定的功能，也消耗一定的时间，外部循环让这些程序段反复迭代直至收敛。从内部开始分析，和声搜索聚类中心需要的时间为：R（初始化）＋k（中心数）×d（维度）×S（式 （4）的演奏＋式 （5）和式 （6）的调音）＋F（式 （3）的适应度计算n×k）＋U （更新和声库）＋P（式 （7）和式 （8）的大概率调音），由于有了寻找最佳聚类中心数的半监督过程，该算法重复了次和声搜索聚类，另外还有式 （1）的维度加权和式（2）数据归一化，因此对于整个半监督聚类而言，整个算法复杂度为。除了适应度公式之外，和声搜索的这些公式都不太复杂，计算速度可以得到保证。

PSO聚类的空间复杂度为O （k＊C＊ （N＋1）），时间复杂度为O （k＊m＊C＊n），总体复杂度为O （k＊C＊（N＋1）＋k＊m＊C＊n）。其中k为粒子个数，C为需要类别数，N为数据维数，n为样本数，m为各类样本的均值向量数。由于FCM没有采用多个粒子搜索聚类中心，因此其算法复杂度为O （C＊ （N＋1）＋m＊C＊n）。文献［6］采用了和声搜索和Kmeans的结合，文献 ［10］在和声搜索聚类时考虑了特征选择，因此二者的算法复杂度均为：O（W＋＊ （R＋k＊d＊S＋k＊ （N＋1）＋m＊k＊n＋n＊k＋U））。从理论上看，除FCM在复杂度上比本文提出的算法有优势外，其余的算法复杂度都比本文的较高。

4 算法性能比较

我们把本文的HSW和FCM、PSO聚类、文献 ［6］和文献 ［10］算法进行比较，测试数据来自4种Benchmark数据，分别是：分为3类有150个4维数据的Iris，分为6类有871个3维数据的Vowel，分为2类有768个8维数据的Diabetes，分为3类有178个13维数据的Wine。由于上述几种算法的性能均与初始值有关，因此我们每种算法分别测试10次，取其平均性能参数进行比较。

对于每种数据集测试时性能参数取：①测试中的最佳聚类中心的聚类评价函数值，②测试中的平均聚类评价函数值，③测试中的最差聚类评价函数值，④获得最佳聚类中心的平均收敛时间。

这次比较实验在Intel Pentium Dual－Core CPU T2310 1.46GHz 1.46GHz，1G内存的计算机上运行，上述算法的代码使用Eclipse 3.5.2的Java语言编写。

Iris数据集测试与性能比较结果见表1。

由于Iris数据量最少，维度也低，被分为3类，因此各种算法聚类效果都比较理想。

Vowel数据集测试与性能比较结果见表2。

表1 Iris数据集测试与性能比较结果

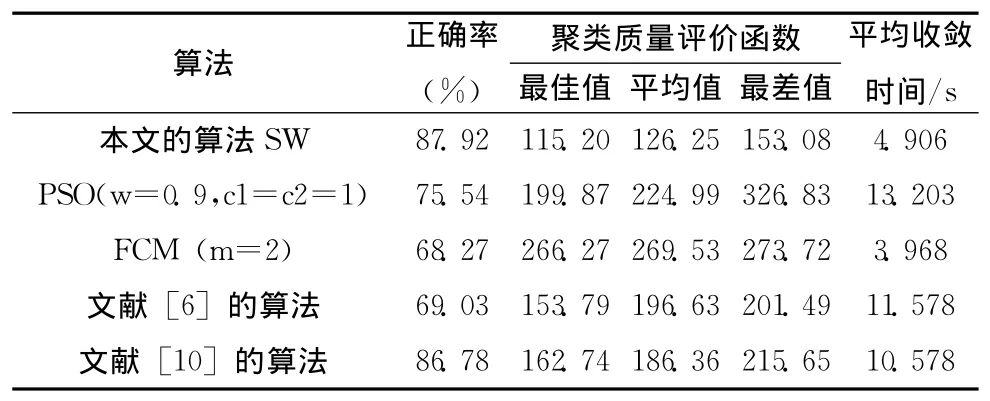
表2 Vowel数据集测试与性能比较结果

由于Vowel数据量最多，但是维度不高，被分为6类，类之间的差别比较大，因此本文算法聚类效果也比较好。Diabetes数据集测试与性能比较结果见表3。

表3 Diabetes数据集测试与性能比较结果

由于Diabetes数据量比较大，维度比较高，却仅分为2类，因此类之间的差别比较小，因此几种算法聚类效果都不太好。

Wine数据集测试与性能比较结果见表4。

表4 Wine数据集测试与性能比较结果

Wine和Iris类似，数据量少，也分为3类，但维度最高，为计算增加了难度，各种算法聚类效果仍然比较可以接受。

从上面的比较可以看出，本文这种算法聚类质量比较高，而且耗时较少。虽然FCM算法速度更快，但是误差较大。因此我们采用本文的算法进行并行处理器性能聚类。

5 并行处理器性能聚类分析

为了分析和识别大规模科学计算中各处理器性能瓶颈。我们这里用回旋电磁数值实验代码 （gyrokinetic electromagnetic numerical experiment，GENE）进行并行计算，GENE代码通过迭代求解具有5维相空间的非线性回旋方程，用于识别电磁等离子聚变产生的涡流特征。GENE可以运行在拥有大量处理器的超级计算机上，代码用MPI并行化的Fortran95实现。数据采集实验在ALTIX超级计算机上进行，GENE代码其中的1024核中运行。通过测试可以收集GENE的不同代码区域的各种MPI属性值和可伸缩性，比如：节点性能，负载能力，信息组织方式，等等。示例数据如下所示：

＜property cluster＝"false"ID＝"7－511"＞

＜name＞Excessive MPI communication time＜/name＞

＜context FileID＝"7"FileName＝"velo.f"RFL＝"33"Config＝"256x1"Region＝"CALL＿REGION"RegionId＝"7－556"＞

＜execObj process＝"247"thread＝"0"/＞

＜/context＞

＜severity＞54.36＜/severity＞

＜confidence＞1.00＜/confidence＞

＜addInfo＞

＜CallTime＞60866＜/CallTime＞

＜PhaseTime＞111959＜/PhaseTime＞

＜/addInfo＞

＜/property＞

＜property cluster＝"false"ID＝"1－17"＞

＜name＞IA64Pipeline Stall Cycles＜/name＞

＜context FileID＝"5"FileName＝"main.f"RFL＝"63"Config＝"256x1"Region＝"USER＿REGION"RegionId＝"5－584"＞

＜execObj process＝"29"thread＝"0"/＞

＜/context＞

＜severity＞40.40＜/severity＞

＜confidence＞1.00＜/confidence＞

＜addInfo＞

＜/addInfo＞

＜/property＞

我们首先将这些数据进行分析，对于处理器有其编号process唯一确定，由于ID唯一表示了该CPU出现性能瓶颈的名称，而RegionID则唯一标示了GENE代码中出现性能瓶颈的区域位置，ID和RegionID的结合就可以确定GENE的哪一部分代码运行时出现了什么样的性能问题，而严重程度就是serverity。因此上述XML文件中，需要提取出来进行用于聚类的属性为：process，ID，RegionID，serverity。我们对这些属性进行构造，就是由给定的属性构造和添加新的属性，以有利于聚类。比如，我们根据属性ID和RegionID可以构造Performance属性。通过这种组合属性，属性构造可以发现关于数据属性间联系的丢失信息，这对知识发现有用的。于是我们构建了如下1024行39列的数据矩阵。

性能分析数据见表5。

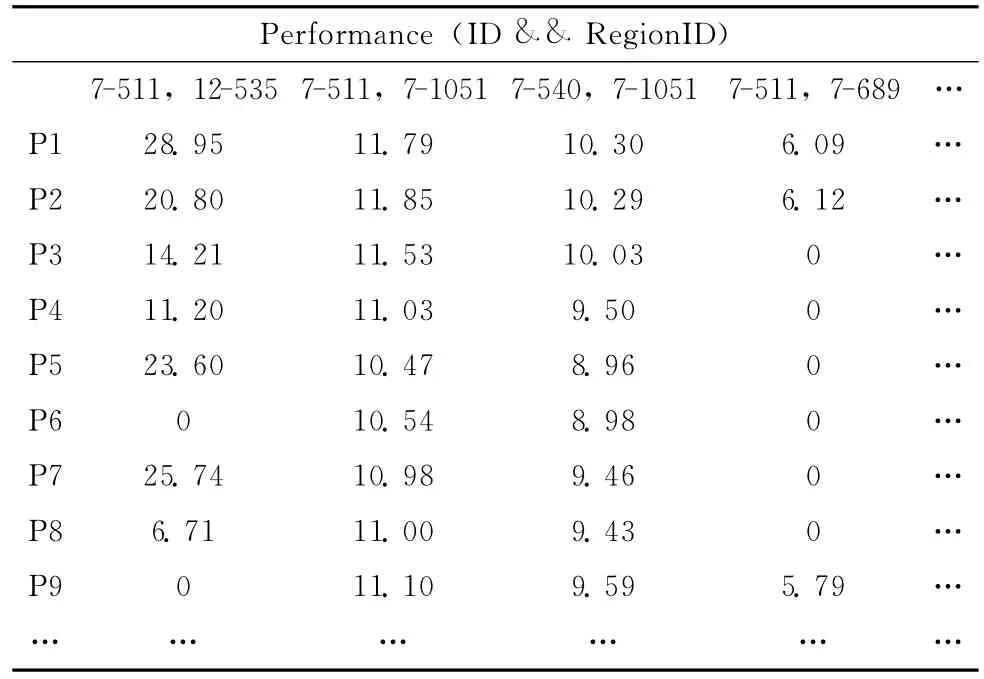
表5 性能分析数据

利用这些数据，我们运用HSC算法对这1024个处理器进行聚类分析，将瓶颈性能近似的处理器归为同一类，聚类的结果就是这1024个处理器被自动分为8类。

并行性能聚类结果见表6。

表6 并行性能聚类结果

图2中的横坐标是处理器的编号，纵坐标是类别。根据这样的聚类，可以重新分配GENG的代码区域到处理器上，取得更好的计算性能。

例如：p1，p20，p140，p230，p663，p915，…，被归为一类，这一类的中心按照Serverity的大小排序为：54.36，52.22，43.36，43.17，40.71，20.34，18.46，7.71，…，按照Serverity的大小排序，这一类主要的瓶颈问题就是：

（1）Serverity值54.36：CALL＿REGION 程序段 （7－556）出现了Excessive MPI communication time性能问题（7－511）；

（2）Serverity值52.22：CALL＿REGION 程序段 （7－556）出现了Excessive MPI time in receive due to late sender性能问题 （7－518）；

图2 处理器聚类结果

以此类推。有了这些性能特征，程序管理员或开发者就可以针对这任何一类处理器的任务重新做出分配或调整。

6 结束语

将随机启发式搜索算法之一的和声搜索算法运用于聚类中，仅仅保留了聚类的评价函数，改变了聚类的方式，从而提高了聚类的质量，本文尝试对其做了一些改进，和其它的算法相比，本文的HSW的半监督聚类有如下优点：

（1）通过半监督学习，算法能够自动找到正确或合理的聚类中心数；

（2）通过特征属性加权，改变了每一维对聚类结果的影响，提高了聚类准确性；

（3）在算法运行后期采用大概率调音保证了算法不会收敛到局部极小。

进一步的工作：这种算法毕竟是一种随机启发式搜索最优聚类中心算法，对于大数据集或高维数据聚类而言，收敛速度始终是一个问题，是否可以将代表不同聚类中心数的和声库分配给不同的进程或线程分布式计算其聚类中心？这种启发式随机搜索算法具有天然并行性，因此本文认为分布式和声搜索聚类算法是可行的，必然提高收敛速度。

［1］LUO Yin－sheng，LI Ren－hou，ZHANG Wei－xi.Clustering algorithm based on clone selection theory ［J］.Control and Decision，2006，20 （11）：1261－1264 （in Chinese）. ［罗印升，李人厚，张维玺.一种基于克隆选择的聚类算法 ［J］.控制与决策，2005，20 （11）：1261－1264.］

［2］XU Xiaohua，CHEN Ling.An adaptive ant clustering algorithm ［J］.Journal of Software，2006，17 （9）：1884－1889（in Chinese）. ［徐晓华，陈崚.一种自适应的蚂蚁聚类算法［J］.软件学报，2006，17 （9）：1884－1889.］

［3］LI Shuai，WANG Xin－jun，GAO Dan－dan.PSO clustering algorithm based on internal spatial characteristic ［J］.Computer Engineering，2009，35 （5）：197－199 （in Chinese）. ［李帅，王新军，高丹丹.基于内部空间特性的PSO聚类算法 ［J］.计算机工程，2009，35 （5）：197－199.］

［4］Santos Coelho L d，de Andrade Bernert D L.An improved harmony search algorithm for synchronization of discrete－time chaotic systems［J］.Chaos，Solitons and Fractals，2009，41（15）：2526－2532.

［5］Osama Alia，Rajeswari Mandava，Mohd Aziz.A hybrid harmony search algorithm for MRI brain segmentation ［J］.Evolutionary Intelligence，2011，4 （1）：31－49.

［6］Forsati R，Meybodi M R，Mahdavi M，et al.Hybridization of K－means and harmony search methods for web page clustering［C］.International Conference on Web Intelligence and Intelligent Agent Technology，Sydney，Australia：IEEE Computer Society，2008：329－335.

［7］Ayvaz M T.Simultaneous determination of aquifer parameters and zone structures with fuzzy c－means clustering and meta－heuristic harmony search algorithm ［J］.Advances in Water Resources，2007，30 （11）：2326－2338.

［8］Weiguo S，Xiaohui L，Fairhurst M.A niching memetic algorithm for simultaneous clustering and feature selection ［J］.IEEE Trans on Knowledge and Data Engineering，2008，20（7）：868－879.

［9］Zeng H，Cheung Y M.A new feature selection method for Gaussian mixture clustering ［J］.Pattern Recognition，2009，42 （2）：243－250.

［10］Sarvari H，Khairdoost N，Fetanat A.Harmony search algorithm for simultaneous clustering and feature selection ［C］.International Conference of Soft Computing and Pattern Recognition.Paris， France：IEEE Computer Society，2010：202－207.

［11］Huang J Z，Ng M K，Rong H，et al.Automated variable weighting in k－means type clustering ［J］.IEEE Trans Pattern Anal Mach Intell，2005，27 （5）：657－668.

［12］Yu Z，Wong H S.Genetic based k－means algorithm for selection of feature variables ［C］.International Conference on Pattern Recognition.Hong Kong，China：IEEE Computer Society，2006：744－747.

［13］Anil Kumar Tiwari，Lokesh Kumar Sharma，Rama Krishna G.Entropy weighting genetic k－means algorithm for subspace clustering ［J］.International Journal of Computer Applications，2010，7 （7）：27－30.

［14］Jing L，Ng M K，Huang J Z.An entropy weighting k－means algorithm for subspace clustering of high dimensional sparse data ［J］.IEEE Trans on Knowledge and Data Engineering，2007，19 （8）：1026－1041.

［15］Domeniconi C，Gunopulos D，Ma S，et al.Locally adaptive metrics for clustering high dimensional data ［J］.Data Mining and Knowledge Discovery，2007，14 （1）：63－97.