基于结构继承的贝叶斯网结构学习优化设计
2012-07-25曾杰鹏谷志元
曾杰鹏,廖 芹,谷志元
(1.华南理工大学 理学院,广东 广州510640;2.广州铁路职业技术学院 应用数学教研室,广东 广州510430)
0 引 言
贝叶斯网络结构学习是贝叶斯网络研究的一个重要方向,尤其在没有先验网络结构的情况下,结构学习算法在建网上的作用尤为突出。贝叶斯结构学习主要有基于评分的启发式算法以及基于互信息等规则[1]的建网方法。其中,基于评分的启发式算法在当前的研究中最为活跃,主要包括爬山算法[2],蚁群算法[3],遗传算法[4],模拟退火算法[5]等。同时,通过对上述算法的优化组合,也生成了各种有效的组合算法,如遗传算法与模拟退火算法的组合算法[6],遗传算法与蚁群算法的组合算法[7]等。
遗传算法搜索范围大,寻优效率高,在贝叶斯网络结构学习中具有普遍的应用。然而由于传统的个体编码主要采用贝叶斯网络的邻接矩阵,导致种群初始化的过程中,可行解的生成概率较低,需要重复生成新个体,以保证其通过无环性检验[8]。其次,在种群的进化过程中,个体的可行性可能受到破坏。因此,对于新生成的个体,往往又需要重新进行无环性检验,进而将非法结构修正为有向无环图[9],或者为非法结构设置较低的适应度,从而降低了寻优的效率[10-11]。另外,之前的研究在计算新个体的结构得分时,往往需要计算整个新贝叶斯网络的得分。然而事实上,在遗传进化过程中,贝叶斯网络通常存在局部不变性。因此可以结合结构得分的可分解性与结构局部稳定性[12],从而进一步优化结构学习的效率。
本文针对上述问题,提出一种新的个体编码方式,同时结合遗传进化过程中,个体的家族得分具有可继承性,从而设计相应的改进算法。最后通过对比实验表明,相比于传统的遗传算法,本文改进的算法在结构学习的精度与效率上都得到明显的提升。
1 贝叶斯网络结构编码的改进
1.1 传统编码的问题
贝叶斯网络结构的传统编码,一般以0-1向量表示。具体如下:若贝叶斯网络有n个节点,其邻接矩阵为(cij)nxn。若节点i指向节点j,则cij=1,表示节点i为节点j的父节点,否则cij=0。把上述邻接矩阵改写为0-1向量 (c11,c12,…,c1n,c21,c22,…,c2n,…,cn1,cn2,…cnn),即可将其作为贝叶斯网络结构的个体编码。
然而在该编码下,得到有向无环图的可能性不高。因为对于节点数为n的贝叶斯网络,所有可能结构的个数f(n)满足[13]
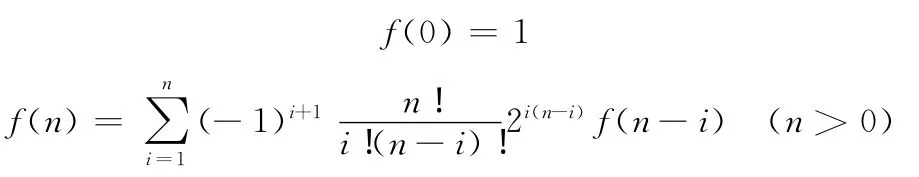
而以随机生成的邻接矩阵为例,所有n阶0-1矩阵的个数F(n)=2nxn。于是,随机生成的邻接矩阵满足无环性的概率。
以n=1,2,……,5为例,计算r(n),见表1。
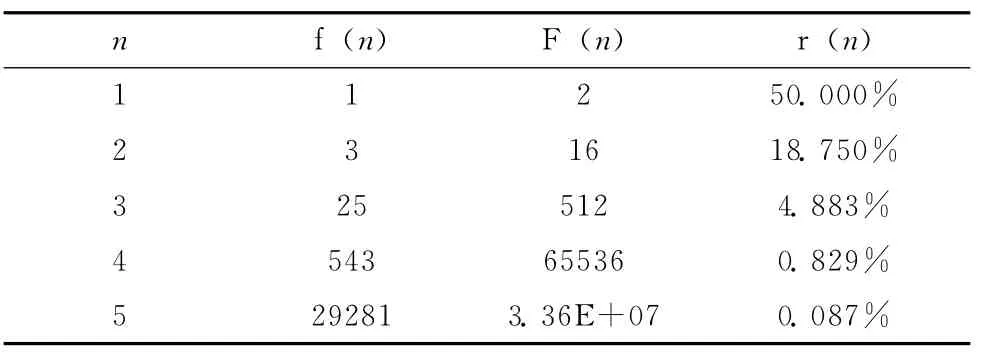
表1 满足无环性的概率
可见,随着节点数的增大,随机生成的邻接矩阵满足无环性的概率迅速减小。
1.2 个体编码改进
考虑到传统个体编码的低效性,本文基于每个贝叶斯网络都可以至少对应到一个节点顺序的事实[14],提出一种新的个体编码方式。该编码包括两个部分:节点顺序与给定节点顺序下的连边情况。
具体设计如下:若节点数为n,个体编码为 (i1,i2,…,in,c12,c13,c23,c14,c24,c34,…,c1n,c2n,…,cn-1,n)。其中i1,i2,…,in为1至n的一个排列,表示节点顺序。为了保证无环性,这里规定只允许排序在前的节点指向排序在后的节点。c12,c13,c23,c14,c24,c34,…,c1n,c2n,…,cn-1,n表示在给定节点顺序下的连边情况。若节点ij指向节点ik(j<k),则cjk=1,否则cjk=0。
例如,当n=4,若编码为 (2,4,3,1,1,1,0,0,1,1)。那么,其中2,4,3,1表示节点顺序,分别对应于变量X2,X4,X3,X1。1,1,0,0,1,1表示给定节点顺序下的连边情况。X2排在第一位,因此没有父节点;X4连边情况的相关编码为1,表示X2为其父节点;X3连边情况的相关编码为1,0,表示X2为其父节点;X1连边情况的相关编码为0,1,1,表示X4,X3为其父节点。于是,该编码对应的贝叶斯网络如图1所示。
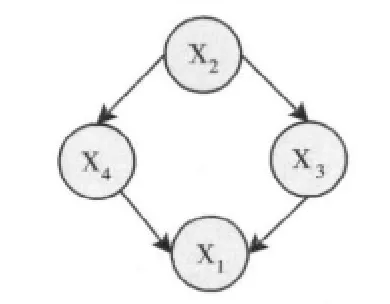
图1 编码对应结构
可以证明,该设计下的个体编码,唯一对应到一个有向无环图,即唯一对应到一个贝叶斯网络;而任意一个贝叶斯网络,都至少可以找到一个该设计下的个体编码与之对应。
该编码设计的好处还在于可以有效减少编码长度。对n个节点的贝叶斯网络,若采用传统方式的编码,其编码长度L(n)=n2,而采用本文设计的编码,计算得知其编码长度L’(n)=n(n+1)/2。可以证明:
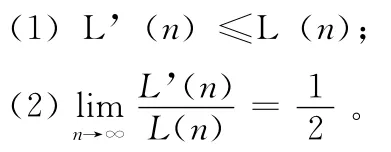
由此说明,本文设计的个体编码可以有效减少编码长度,降低存储开销。而且当节点数增大时,本文编码的优势更加明显,可以将编码长度减少到将近传统编码的一半。
2 基于家族继承的评分算法改进
2.1 评分函数的改进
关于贝叶斯网络结构的优劣存在多种评价标准,当前以BIC得分最为常用。BIC得分的计算方式如下[15]
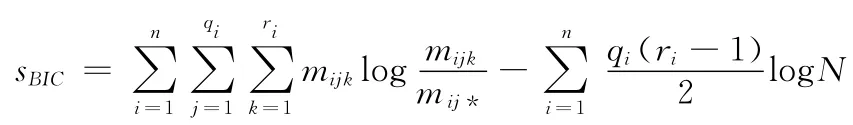
式中:n——节 点 数,qi——节 点i的 父 节 点 取 值 数,ri——节点i的取值数,mijk——学习样本中,父节点为第j种取值下,节点i为第k种取值的样本数。。N表示样本数。
在传统的遗传算法中,由旧种群生成的新种群,其中新个体的结构得分往往整个重新计算。然而分析发现,这个过程可能存在重复运算的问题。例如对于节点数为4的贝叶斯网络,遗传前后可能存在网络结构分别如图2所示。
那么,传统方法计算该新结构的得分,需要先分别计算X1,X2,X3,X4的家族得分。然而观察发现,在新结构中X1和X3的父节点,与旧结构的中一致,因此它们的家族得分可以直接从旧结构中继承。于是只有X2和X4的家族得分需要重新计算,从而大大简化了结构得分的计算。

图2 新旧个体对应结构
2.2 改进算法实现
本文采用矩阵AllPa和AllFamS,分别对上一代所有个体中各节点对应的父节点及家族得分进行存储。AllPa=(Paij)mxn,其中m表示种群大小,n表示网络节点数,Paij表示个体i中节点j的父节点的集合。若个体i的节点j无父节点,则记Paij= {0}。AllFamS= (FamSij)mxn,其中FamSij表示个体i中节点j的家族得分。因此,计算个体i的结构得分只需对AllFamS第i行求和。
对于遗传过程中生成的新个体,计算其结构得分时,需要累积其各节点的家族得分。例如计算节点i的家族得分,则首先对比该节点i与父代中个体的节点i,确定其父节点集合是否存在一致,如果存在,则直接从上一代的该个体继承节点i的家族得分,如果不存在,则需通过重新扫描样本集计算。
AllPa和AllFamS的更新算法具体如下:
Update//更新算法
输入:AllPa,AllfamS,Population//种群,data//数据集
输出:NewAllPa,NewAllfamS
//获取各个体的各父节点
fori=1:m//m为种群个体数
//针对某一个体,获取其各节点的父节点
forj=1:n//n为节点数
Pa=GetPa(Population,i,j)//GetPa (Population,i,j)返回种群Population的个体i中节点j的父节点集合
ifPa=Γ
NewAllPa{i,j}=0;
else
NewAllPa{i,j}=Pa;
end
end
end
//计算各个体的各家族得分
fori=1:m
//针对某一个体,计算其各节点的家族得分
forj=1:n
Exist=false;//Exist为能否家族继承的标志
//扫描上一个种群的AllPa,确定能否家族继承
fork=1:m
ifNewAllPa{i,j}==AllPa{k,j}
NewAllfamS(i,j)=AllfamS(k,j);
Exist=true;
break;
end
end
//如果无法家族继承,家族得分则需重新扫描data计算
ifExist=false;
NewAllfamS(i,j)=GetfamS (data,j,Pa);//GetfamS(data,j,Pa)返回根据数据集data计算得到的节点j在父节点Pa下的家族得分
end
end
end
3 结构学习遗传算法的改进
基于上文的个体编码设计与家族继承方法,下面设计与之相应的结构学习遗传算法。该算法设计的难点在于交叉与变异过程中对个体无环性的保证。具体如下:
3.1 种群初始化
设种群大小为m,按照上文的个体编码方式,生成m个个体。个体生成的具体步骤如下:
步骤1 随机生成1至n的一个排列i1,i2,…,in,表示节点的顺序;
步骤2 生成一个 (n-1)*n/2维的零向量,表示给定节点顺序下的连边情况;
步骤3 将步骤1中的n维向量与步骤2中的 (n-1)*n/2维向量连接,则形成n* (n+1)/2维的个体编码。
该种群初始化的设计表明,所有个体的初始状态均无连边,初始个体之间的差异在于节点顺序的不同。
3.2 适值函数
个体的适值是通过对其BIC得分进行0-1压缩得到的,即个体i对应的适值f(i)为
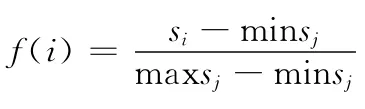
式中:si——个体i的BIC得分。
3.3 选择算子
本文的选择算子主要采取μ+λ策略,具体设计如下:
步骤1 保存上一代的所有个体及其适值;
步骤2 采用轮盘赌算法从上一代的所有个体中挑选m个形成新种群;
步骤3 合并上一代个体与交叉变异后的新种群个体,从中选择适值最高的前m个。
因此本文选择算子的设计,引入了父代与子代的竞争,在个体选择方面,还采用了以适值排序与轮盘赌概率相结合的方式。
3.4 交叉算子
交叉算子采用单点交叉。假如交叉的位置出现在表示连边情况的0-1编码部分,则直接将从该位置起的后半段相互交换。如果交叉的位置出现在表示节点顺序的编码部分,则首先将表示连边情况的整段0-1编码相互交换,再进行表示节点顺序的编码的交叉。
节点顺序编码的交叉方式如下:假设节点顺序S1=(i1,i2,…,in),S2= (j1,j2,……,jn)。若交叉位置为p,则首先将两节点顺序转化为S1= (i1,i2,……,ip-1,jp,jp+1, ……,jn,ip,ip+1, ……,in),S2= (j1,j2,……,jp-1,ip,ip+1,……,in,jp,jp+1,……,jn),接着按从左到右的顺序,扫描S1和S2中的每个节点,如果该节点在其左边的子串中已经出现,则将其删去,直至S1和S2最终形成两个新的节点顺序。
例如对于节点数为5的两个节点顺序S1= (2,3,1,4,5),S2= (5,3,4,1,2)。若交叉位置为3,则首先将S1和S2转化为S1= (2,3,4,1,2,1,4,5),S2=(5,3,1,4,5,4,1,2),再按照上述规则进行删减,得到S1= (2,3,4,1,5),S2= (5,3,1,4,2)。
于是,通过该交叉算子的设计,保证了交叉运算后新个体的可行性。
3.5 变异算子
变异算子采用单点变异。假如交叉的位置出现在表示连边情况的0-1编码部分,则直接将该位置的编码0变1或1变0。如果交叉的位置出现在表示节点顺序的编码部分,则随机选择另一节点,将两节点的位置互换。
因此,对于个体编码 (i1,i2,…,in,c12,c13,c23,c14,c24,c34,…,c1n,c2n,…,cn-1,n),该变异算子包括如下3种变换:
变换1:若进行变异的编码为cij,且cij=0,则变异表示添加节点i指向节点j的边;
变换2:若进行变异的编码为cij,且cij=1,则变异表示删除节点i指向节点j的边;
变换3:若进行变异的编码为ij,且选中的与之交换的编码为ik,则变异表示在贝叶斯网络结构中,直接互换节点ij与节点ik,而不改变其它连边情况。
例如,个体编码 (2,4,3,1,1,1,0,0,1,1)对应的结构如图3(a)所示。若互换节点2与节点3的位置,则得到新个体编码 (3,4,2,1,1,1,0,0,1,1),其对应的结构如图3(b)所示。
可见,在编码中互换节点2与节点3的位置,就相当于在贝叶斯网络结构中直接互换节点2与节点3。
于是,通过该变异算子的设计,保证了变异运算后新个体的可行性。
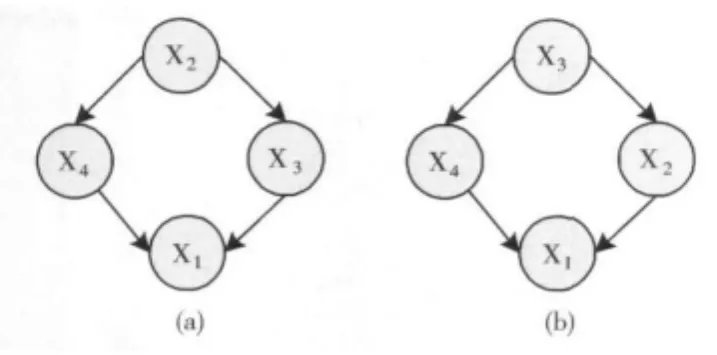
图3 新旧编码对应结构
4 实验结果
下面对原始遗传算法 (OldGA)与本文改进的遗传算法 (NewGA)进行对比试验。
数据集来自Aisa网络。该网络的节点数为8,边数为8。
令种群大小为10,交叉概率为0.9,变异概率为0.1。遗传算法的终止条件为运行时间达到事先给定的算法耗时上限。
为了减少遗传算法单次运行随机性的影响,对于每个随机试验,OldGA与NewGA都重复进行10次,最终取这10次中各指标的平均值,作为OldGA与NewGA该试验的结果。
取定样本量为1000,在给定不同的算法耗时上限的情况下,对比新旧算法的建网效果。
4.1 最优得分与算法耗时
最优得分是指进化过程中最优个体的得分,它与算法耗时的关系如图4所示。
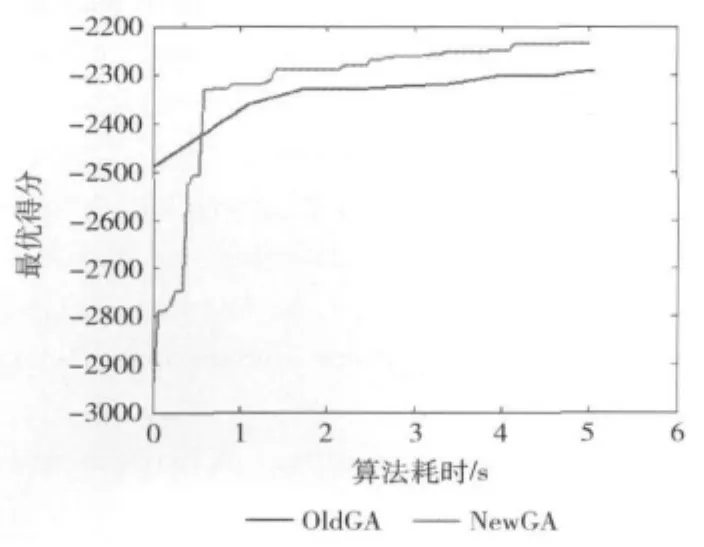
图4 最优得分与算法耗时
可见一开始,NewGA的最优得分低于OldGA,然而NewGA具有较高的进化效率,因此其最优得分在随后就迅速超过了OldGA。
4.2 边误差与算法耗时
边误差是指在标准网络中存在,而算法生成的网络中不存在或者标准网络中不存在,而算法生成的网络中存在的连边数目总和,它与算法耗时的关系如图5所示。
可见,OldGA和NewGA的边误差总体上均随算法耗时呈下降趋势,而且相比发现,NewGA的边误差明显小于OldGA,而且其下降的速度也更快。
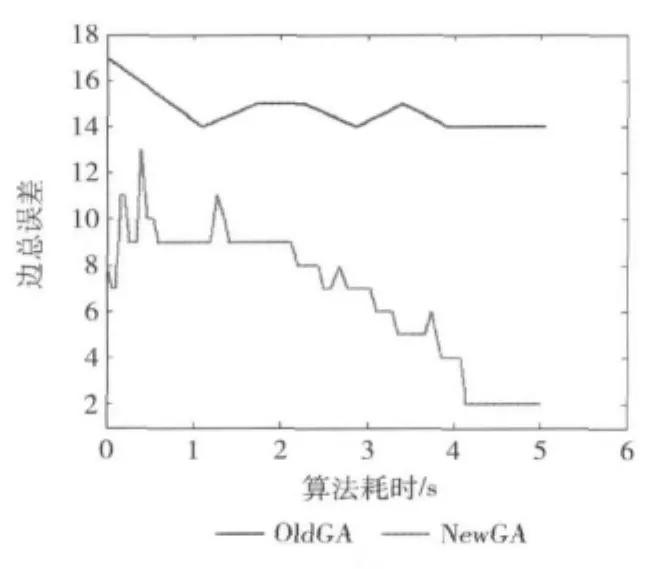
图5 边误差与算法耗时
5 结束语
本文针对贝叶斯网络结构学习中,传统遗传算法的个体编码需要反复验证无环性的问题,提出了一种新的个体编码方式,将网络节点排序与基于给定排序的节点间连边情况分别编码,从而提高了个体编码在遗传过程中的可行性。同时,考虑到进化过程中,结构得分的可分解性以及父代家族得分的可继承性,提出了基于家族继承的结构评分算法改进,在此基础上设计了相应的改进遗传算法。通过实验表明,本文算法在建网的精度与效率上都得到了明显的提升。
[1]GOU Kui-xiang,GONG Xiu-jun,ZHAO Zheng.Learning Bayesian network structure from distributed homogeneous data[C].Eighth ACIS International Conference on Software Engineering,Artificial Intelligence,Networking,and Parallel/Distributed Computing.Qingdao:IEEE,2007:250-254.
[2]JIN Xiaobo,HOU Xinwen,LIU Cheng-lin.A hybrid generative-discriminative learning algorithm for Bayesian network structure[C].Proceedings of the International Conference on Wavelet Analysis and Pattern Recognition.Beijing:IEEE,2007:618-623.
[3]WANG Fengshan,ZHU Wanhong.A Bayesian network structure learning method based on ant colony algorithm [C].International Conference on Management and Service Science.Wuhan:IEEE,2010:1-4.
[4]ZHOU Benda,TIAN Xu.An algorithm for Bayesian networks structure learning based on genetic algorithms and reinforcement learning [J].Microcomputer & Its Applications,2007,6(S1):2257-2259 (in Chinese).[周本达,田旭.基于遗传算法和强化学习的贝叶斯网络结构学习算法 [J].微型机与应用,2007,6 (S1):2257-2259.]
[5]GUO Peng,LI Naixiang.An EM-MCMC algorithm for Bayesian structure learning [C].2nd IEEE International Conference on Computer Science and Information Technology.Beijing:IEEE,2009:158-162.
[6]CAO Weidong,FANG Xiangnong.An improved method for Bayesian network structure learning [C].Sixth International Conference on Natural Computation.Yantai:IEEE,2010:3133-3137.
[7]LI Xi-jun.Learning structure of Bayesian network using ant colony algorithm assisted by genetic algorithm [C].Intelligent Systems and Applications.Wuhan:IEEE,2009:1-4.
[8]CHEN Wangyu,QIN Liao.Research on Bayesian network adaptive knowledge construction and inference based on genetic algorithm [C].Fourth International Conference on Natural Computation.Jinan:IEEE,2008:315-319.
[9]LI Xian-jie,ZHANG You-sheng,LI Jianfei.Algorithm of BN structural learning based on quantum genetic [J].Application Research of Com-puters,2008,25 (4):996-1002 (in Chinese).[李显杰,张佑生,李剑飞.基于量子遗传算法的贝叶斯网络结构学习 [J].计算机应用研究,2008,25 (4):996-1002.]
[10]HUANG Hao,SONG Hantao,LU Yuchang.Research on structure learning algorithm of Bayesian networks based on niche genetic algorithm [J].Application Research of Computers,2007,24 (4):100-103 (in Chinese).[黄浩,宋瀚涛,陆玉昌.基于小生境遗传算法的贝叶斯网络结构学习算法研究 [J].计算机应用研究,2007,24 (4):100-103.]
[11]LI Weiwei,WANG Jiandong,FANG Liming,et al.Edgeoriented approach of Bayesian networks based on tabu genetic algorithm [J].Computer Engineering,2009,35 (12):178-180(in Chinese). [李玮玮,王建东,方黎明,等.基于遗传禁忌算法的贝叶斯网边定向方法 [J].计算机工程,2009,35 (12):178-180.]
[12]Valentin Ziegler.Approximation algorithms for restricted Bayesian network structures [J].Information Processing Letters,2008,108 (2):60-63.
[13]Lobna Bouchaala,Afif Masmoudi,Faiez Gargouri,et al.Improving algorithms for structure learning in Bayesian networks using a new implicit score [J].Expert Systems with Applications,2010,37 (7):5470-5475.
[14]CHENG Zekai,QIN Feng,YANG Bo.Improving Bayesian network structure learning with mutual information-based node ordering in the k2algorithm [C].Proceedings of the 6th World Congress on Intelligent Control and Automation.Dalian:IEEE,2006:6010-6014.
[15]LIU Guixia,FENG Wei,WANG Han,et al.Reconstruction of gene regulatory networks based on two-stage Bayesian network structure learning algorithm [J].Journal of Bionic Engineering,2009,6 (1):86-92.
