基于两次禁忌搜索的军事物资装运方案研究
2012-07-25齐玉东齐玉华谢晓方
齐玉东,齐玉华,谢晓方
(1.海军航空工程学院 计算机教研室,山东 烟台264001;2.国防科学技术大学 计算机学院,湖南 长沙410073)
0 引 言
现代战争中,由于战争的突然性以及战场地点的不确定性,要求我方必须具有强大的军事力量投送能力,从而能及时有效的将战争急需的人员和武器装备物资投入战场,积极抢占战争主导权。在有限的运输资源,如何分配各种资源运输,并在划定的时间段中安全有效的完成特定大量的物资装载与运输问题,显然是局部寻优最小化问题,并已证明是 NP-hard[1-3]。文献 [4]对具有广泛应用背景、多约束条件和求解困难的集装箱装载问题,引入具有人工智能记忆机制、基于邻域搜索而避免局部最优的禁忌搜索算法,探讨了在求解集装箱装载问题中禁忌搜索的编码、解码和邻域解生成等关键技术。文献 [5]根据军事空运装载的特点,建立了空运装载的数学模型,讨论了求解空运装载问题的紧急搜索算法编码、解码、评价函数、邻域操作和禁忌表等关键问题,实现了对空运装载问题的求解。文献 [6]针对物资装载问题提出了一种可变邻域搜索 (VNS)算法,其基于最大空或类禁忌搜索方法对物资装载和运输问题进行研究,但是搜索时间过长,不利于实际应用,本文针对此问题,提出两次禁忌搜索,第一次禁忌搜索生成初始解,然后进行第二次禁忌搜索对初始解进行邻域优化移动。这样通过第一次搜索的较优初始解,限制了第二次禁忌搜索的随机性,使总体搜索过程更快速有效。
1 Tabu简介
1.1 算法概述
禁忌搜索算法思想由Glover等人于1985年最早提出,其是对局部邻域搜索的一种扩展,本质是一种全局逐步寻优算法,是对人类思考问题过程的一种模拟。禁忌搜索为了避免迂回搜索,引入了一个灵活的存储结构和相应的禁忌准则,并通过藐视准则赦免一些被禁忌的优良状态,进而保证多样化的有效搜索以最终实现全局寻优。为了避免重复搜索某些局部最优解,禁忌搜索维持一个禁忌表,根据特定算法标记一些局部最优解,并在后续搜索过程中跳过已标记过得最优解,从而保证对不同的有效搜索途径进行搜索,因此具有较强的爬山能力[7]。禁忌搜索涉及到邻域、禁忌表、禁忌长度、候选解、藐视准则等参数概念。
对上述基本算法的修改则衍生了各种版本的改进禁忌搜索算法,如根据调整禁忌长度的算法不同,可分为自适应禁忌搜索 (ATS)和反应禁忌搜索 (RTS)算法[8]。
1.2 算法基本思想
基础禁忌搜索算法的基本流程如下[9-10]:
(1)设定参数值,随机生成初始解x,bestsofar=x,并将禁忌表设置为空。
(2)若终止条件成立,终止算法并输出结果,否则,继续搜索。
(3)利用当前解的邻域函数抽样生成若干邻域解,并从中根据目标函数确定若干候选解。
(4)判断是否满足藐视准则,若满足,则用满足藐视准则的最优解替换当前解,同时将此最优解对应的对象列入禁忌表,并替换bestsofar值,转入步骤 (6),否则继续。
(5)根据候选解对应对象的禁忌属性,搜索禁忌表,将非禁忌对象中的最佳状态确认为当前解,并根据 “先入先出”原则,替换禁忌表中的禁忌对象。
(6)转步骤 (2)。
上述算法过程为禁忌搜索的基础,可以对具体环节进行精化和改进,构造出多种新的禁忌搜索算法。其中,算法中所述禁忌对象,可以是具体的搜索操作,也可以是搜索状态和搜索目标值等等。
2 基于禁忌搜索算法的物资装载与运输问题
一般的,将运输方式分为空运、陆运和水运3种方式。由于空运具有较大的时间优势,能够将重要的物资以最快的速度运达目的地,因此3种运输方式首先考虑空运。但是相对陆运和水运,空运又具有负荷载重低,有效利用空间小,可用数量有限等不利因素,因此必须根据物资的属性 (重量和体积)及重要性,使用禁忌搜索算法得出在满足时间限制条件下的成本最小的运输飞机数,若运输飞机数不能满足需求,则将剩余的物资进行陆运和水运。
2.1 物资空运
由于禁忌搜索是一种基于邻域的智能搜索算法,具有一定的随机性,为了使搜索过程更为快速有效,论文使用两次禁忌搜索。不同于一般禁忌搜索随即生成初始解,本文初始解由第一次禁忌搜索输出生成,然后进行第二次禁忌搜索对初始解进行邻域优化移动。
2.1.1 一次禁忌搜索生成初始解
禁忌搜索算法本质是一种基于邻域的方案移动,即在现有方案的领域中选择一个最优,并替换现有方案,因此其初始解并不要求为可行解,但是较优的方案则可以极大减少禁忌算法的搜索时间。具体到空运问题,较优的初始解方案意味着,对于每架飞机,要保证其空间利用和负荷载重货物同时达到最大化。其中空间利用最大化是指货盘数目全部占用,负荷载重货物最大化则是指不可增加货物,否则负荷载重超过飞机额定载重量。本文使用第一次禁忌搜索算法,寻找较优的初始解。
详细步骤如下:
(1)飞机索引变量置0。
(2)若全部飞机已被索引,则结束搜索,否则转 (3)。
(3)找出一架飞机,该飞机的额定载重量与其货盘数量的比值最大。
(4)若①全部物资没有被装入飞机,且②该飞机空间没有被全部利用或载重量没有完全被利用,转 (5),否则转 (2)。
(5)禁忌表操作计数器加1。
(6)若①该架飞机空间没有被全部利用,且②载重量没有完全被利用,转 (7),否则转 (8)。
(7)对于每一组物资,如果将其装入当前选定的飞机时,并不会造成飞机容积和载重量越界,则将该组物资装入飞机。转 (12)。
(8)若该架飞机空间没有被全部利用但载重量已完全被利用,转 (9),否则转 (10)。
(9)依次进行以下操作:①从飞机上取下最重的物资,并将其放回原始物资组;②更新禁忌表;③按照从轻到重的顺序,依次从物资组中,选取重量最轻的物资,直到找到一个物资能被放入飞机或已遍历所有物资组。转 (12)。
(10)若①该架飞机空间已被全部利用,且②载重量没有完全被利用,转 (11),否则转 (12)。
(11)依次进行以下操作:①从飞机上取下最轻的物资,并将其放回原始物资组;②更新禁忌表;③按照从重到轻的顺序,依次从物资组中,选取重量最重的物资,直到找到一个物资能被放入飞机或已遍历所有物资组。转(12)。
(12)若飞机上的物资发生变化,转 (13),否则转(14)。
(13)循环变量置0,转 (15)。
(14)循环变量加1。
(15)若已经循环了10次,飞机上的物资一直没有发生变化,转 (2),否则转 (4)。
由上述流程可知,本次搜索的基本思想是使每个飞机的空间利用和负荷载重货物同时达到最大化,但是因为本次搜索没有考虑飞机重心越界问题,因此得出的方案通常为次优,甚至是不可行方案。为了找到满足各个约束的较优可行解方案,需要进行第二次禁忌搜索。
2.1.2 二次禁忌搜索优化初始解
本次禁忌搜索是在第一次搜索得到的初始解的基础上,考虑重心越界问题,其目标是,在满足各种限制的前提下,移向目标函数最小的可行方案。
设物资 (已打包)总数为N,运输飞机总数为M。
(1)目标函数为

限制条件为

λ1,物资未被完全装载时的惩罚系数。
Cj,飞机j的使用成本。

WFj,飞机j的利用率。

λ2,飞机未被充分利用时的惩罚系数。
W_CBj,飞机装入所有物资后的横向重心位置

式中:Wk——物资k的重量,DWk——物资k的重点到飞机重心纵向参考线的距离,Kj——已装入飞机j的物资集合。xj,min、xj,max——飞机j的横向重心边界值。
λ3,飞机横向重心偏离时的惩罚系数。
H_CBj,飞机装入所有物资后的纵向重心位置

式中:Wk——物资k的重量,DHk——物资k的重点到飞机重心横向参考线的距离,Kj——已装入飞机j的物资集合。yj,min、yj,max——飞机j的纵向重心边界值。
λ4,飞机纵向重心偏离时的惩罚系数。
(2)下限解与上限解
下限解为

式中:N——物资总数目,NP—— 一架飞机货舱中的货盘总数,WN——物资的总重量,ACLP—— 一架飞机的额定载重。
上限解为执行空运的部队所能提供的最大运输机数量。
(3)领域操作算法
1)迭代变量初始化。
2)若①持续没有改善的迭代次数不大于规定的次数,且②轻微改善迭代次数不大于规定的次数,且③禁忌迭代次数不大于规定的次数,则转2),否则结束搜索。
3)若全部物资已被装入飞机,则转6),否则转4)。
4)若某个飞机上仍有空的位置,则获得剩余载重能力最大且空位置最多的飞机,否则,找出一架可用的飞机,该飞机的额定载重量与其货盘数量的比值最大。
5)找到未被装入飞机的最重的物资。将其放入飞机。更新禁忌表。
6)若某架飞机的重心偏离越界,转7),否则转8)。
7)重心调整次数加1,调整已装入该架飞机的物资的位置,若调整后没有效果,则撤消调整操作,重心调整次数置0,否则,更新禁忌表,转11)。
8)若①有某架飞机空间没有被全部利用,或②非空飞机的数量大于下限解且对候选解已进行了一定程度的改进,或③非空飞机的数量大于下限解且候选解没有得到一定的改进,转9),否则转10)。
9)从载重量最轻的飞机上取下所有物资,并将取下的最重的物资装入载重量最轻的飞机,更新禁忌表,转11)。
10)在非空飞机之间调换物资,更新禁忌表,转11)。
11)针对候选解计算目标函数值,转2)。
2.2 陆运、水运方式的装载与运输
若空运装载时,运输飞机数量不能满足需求,则将剩余物资按公路、水路方式运输。求解过程如下:
(1)参考运输网络,对每一个物资指定初始解,即每一种物资的起始点、起始时间、到达点、到达时间、运输方式。
(2)根据物资体积和重量计算所需的载具数量。
(3)将晚到的物资按照晚到惩罚度从大到小排序后,生成一个晚到物资清单。
(4)对晚到物资清单中的所有物资在相同的起始点-到达点领域内进行禁忌搜索,得到可减少晚到惩罚度后的物资清单。
(5)重复 (3)、(4)。
(6)重复 (2)。
3 实例求解
海军航空兵某一飞行团实施机动转场到A地 (到达点),所需要的弹药装备型号及时间要求见表1,各个弹药起始点所装运的弹药装备数量、可以采用的运输方式、及各种载具的性能参数分别见表2~表4。
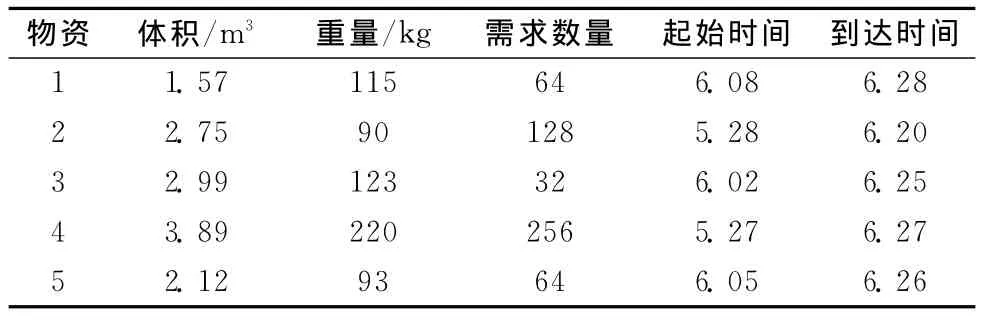
表1 弹药装备型号
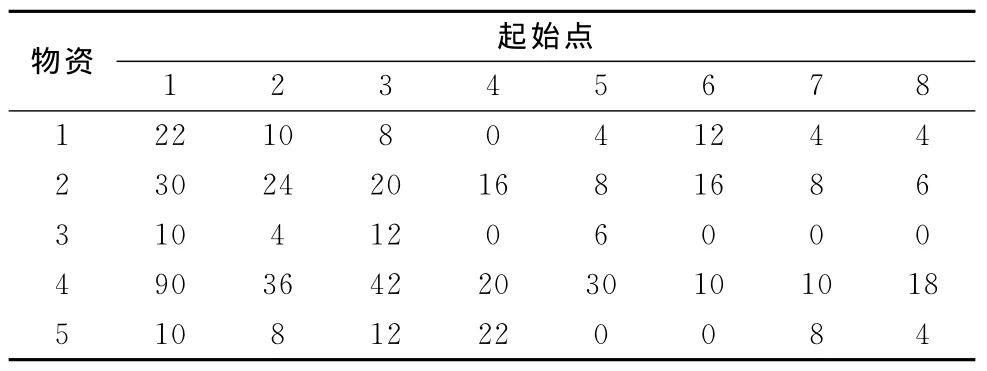
表2 起始点需装运的弹药装备数量

表3 起始点可以使用的载具数量
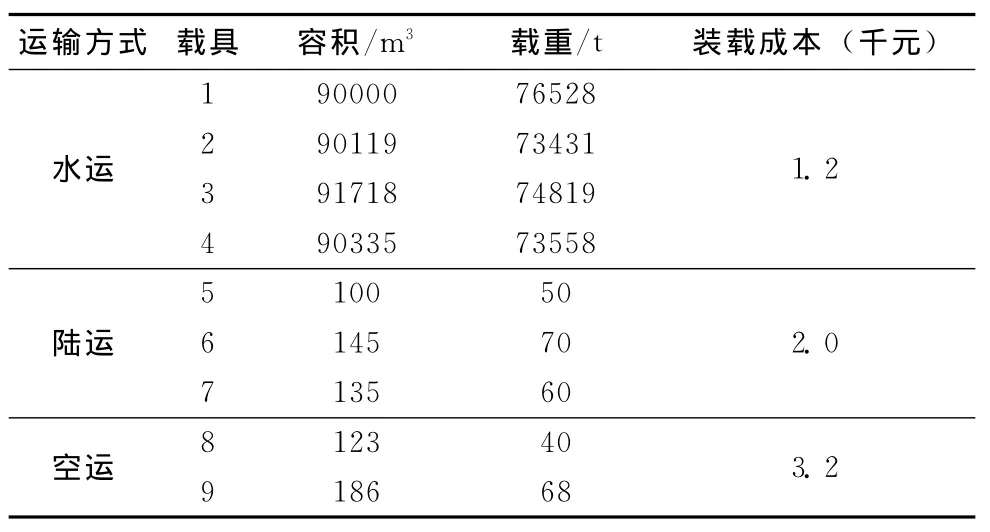
表4 载具性能参数
按照前述进行第一次禁忌搜索,得到最大利用飞机货仓空间和负荷载重货物的初始解方案见表5。

表5 飞机装运方案
将表5所示初始方案作为初始解输入,并取λ1=λ2=λ3=λ4=1,考虑飞机的重心限制问题和陆运、水运综合方式,进行第二次禁忌搜索,得到可行的较优装载方案见表6。

表6 最终装运方案
由表5可知,第一次禁忌搜索得到的方案,最大利用了飞机的货仓空间和负荷载重货物,但由于没有考虑飞机的重心偏移问题,方案并不是可行解,经过第二次禁忌搜索的邻域移动,根据飞机的重心调整了飞机货物载量,并以最小化目标函数为指标,得到表6所示的较优的可行装运方案。
4 结束语
在有限的运输资源,如何分配各种资源运输,并在划定的时间段中安全有效的完成特定大量的物资装载与运输问题,是当前军事力量投射的关键问题之一。本文在总结其它文献的基础上,提出了两次禁忌搜索算法:第一次禁忌搜索生成初始解方案,然后进行第二次禁忌搜索对初始解进行邻域优化移动,得到较优的可行运输方案。通过第一次搜索的较优初始解,限制了第二次禁忌搜索的随机性,使总体搜索过程更快速有效。
[1]Stephen C H Leung,Zhou Xi-yue,Zhang Defu,et al.Extended guided tabu search and a new packing algorithm for the two-dimensional loading vehicle routing problem [J].Computers & Operations Research,2011,38 (1):205-215.
[2]Fuellerer G,Doerner K F,Hartl R F,et al.Metaheuristics for vehicle routing problems with three-dimensional loading constraints [J].European Journal of Operational Research,2010,201 (3):751-759.
[3]ZHANG Tao,ZHANG Yue-jie,TIAN Wen-xin,et al.A residual-loading-capacity-based ant colony system for the vehicle routing problem with simultaneous delivery and pickup [J].Control Theory & Applications,2009,26 (5):546-549 (in Chinese).[张涛,张玥杰,田文馨,等.基于剩余装载能力的蚁群算法求解同时送取货车辆路径问题 [J].控制理论与应用,2009,26 (5):546-549.]
[4]LIU Jia-min,DONG Zong-ran,MA Guang-ni.Solving container loading based on tabu search algorithm [J].Journal of Shenyang University of Technology,2009,31 (2):212-216 (in Chinese).[刘嘉敏,董宗然,马广妮.基于禁忌搜索算法求解集装箱装载问题 [J].沈阳工业大学,2009,31 (2):212-216.]
[5]ZHANG Jun,CHEN Bo-song,WANG Xin-hu,et al.Application of the tabu search algorithm to solving the loading problems in military airlift [J].TrafficEngineering and Technology for National Defence,2010,8 (6):10-13 (in Chinese). [张军,陈柏松,王新虎,等.军事空运装载问题的禁忌搜索算法实现 [J].国防交通工程与技术,2010,8 (6):10-13.]
[6]Parreno F,Alvarez-Valdes R,Oliveira J F,et al.Neighborhood structures for the container loading problem:A VNS imple-mentation [D].University of Valencia,2005:1-21.
[7]Hadi Mashinchi M,Mehmet A Orgun,Witold Pedrycz.Hybrid optimization with improved tabu search [J].Applied Soft Computing,2011,11 (2):1993-2006.
[8]Kaye McKinzie.A tabu search approach to strategic mobility mode selection [D].Austin:University of Texas at Austin,2005:38-39.
[9]SUN Yan-feng.A hybrid strategy based on genetic algorithm and tabu search [J].Journal of Beijing University of Technology,2006,32 (3):258-262 (in Chinese). [孙艳丰.基于遗传算法和禁忌搜索算法的混合策略及其应用 [J].北京工业大学学报,2006,32 (3):258-262.]
[10]ZHANG Shu-rong,SU Bing.Something about tabu search approach [J].Kaoshi Zhoukan,2006 (48):228-228 (in Chinese).[张淑荣,苏兵.谈谈禁忌搜索算法 [J].考试周刊,2006 (48):228-228.]
