基于混沌和细胞自动机的图像加密算法
2012-07-25李元香
彭 川,李元香
(1.武汉大学 软件工程国家重点实验室,湖北 武汉430072;2.中南民族大学 计算中心,湖北 武汉430074)
0 引 言
图像加密是图像安全保护的核心技术和有效手段。数字图像加密的基本方法有像素置乱和像素替换两类。实际应用中,通常将以上两种方式结合进行加密处理。
混沌系统具有类随机、对初始状态和参数的极其敏感等特性,具有良好的密码学特性,非常适合用于信息加密,其安全性依赖于密钥流的随机性。自1989年logistic混沌映射作为密钥发生器用于信息加密以来,低维混沌系统用于信息加密已经得到广泛的研究。但低维混沌系统的动力学特性相对简单,密钥空间容量小,安全性不高,因此研究中更多的是利用超混沌系统即两个以上的混沌系统进行加密可以改善其安全性能,但其实现比一般低维混沌系统复杂。
Von等人在研究具有自组织特性的离散动力系统时引入了细胞自动机 (CA)的概念,1985年,Wolfram最先提出将CA运用于密码学,从此,CA逐渐成为研究密码学的重要方法,也逐渐出现了许多有价值的学术成果[1-5]。国内对CA加密技术的研究也逐渐增多。文献 [6]提出了一种基于初等CA的图像加密算法;文献 [7]进行了二维CA的图像加密方法的研究;文献 [8]利用二维细胞自动机设计了一种双层耦合的伪随机数发生器;文献 [9]提出了一种基于可逆CA的多粒度CA加密模型;文献 [10]研究了一种二维CA的反向迭代加密方法。基于细胞自动机的图像加密的安全性能很大程度取决于迭代规则和邻域半径,因此高维细胞自动机比低维细胞自动机具有更高的安全性,已经一些研究开始针对高维CA展开。研究表明,可以通过提高细胞自动机结构的复杂性来提高密钥流的周期和安全性,但是复杂的结构却大大增加了硬件实现的难度和代价。二维CA的结构相对复杂而又容易硬件实现,所以是研究CA加密系统的理想模型。本文将二维细胞自动机(2D-CA)和混沌理论相结合,提出一种基于二维触发细胞自动机 (2D-TCA)和混沌系统的图像加密算法。该算法是一种结合了像素置乱和像素替换的加密方法。基于混沌系统良好的密码学特性和细胞自动机优异的加密性能,该算法具有较高的加解密效率、较大的密钥空间和较高的安全性能,并且非常便于硬件实现。
1 logistic混沌系统
混沌现象是非线性动力学系统中确定的类随机过程,这种过程是非周期的且又不收敛,但它是有界的,并且对初始状态和系统参数具有极其敏感的依赖性。给定同一个混沌系统两个非常接近的初值或参数,系统经过较短时间后,会产生两组完全不同的互不相关的混沌序列。Logistic映射是一种模型简单的混沌动力系统,以其遍历性、对初值高度敏感性的特点而倍受关注,可用以下非线性方程来描述
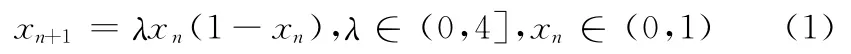
当3.5699456<λ≤4时,系统的动力学形态十分复杂,将进入混沌状态。当λ=4时,logistic混沌序列的概率分布函数ρ(x)为
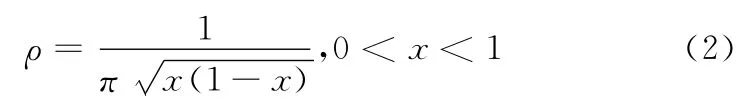
通过该式可以计算出混沌序列轨迹的均值为0,初始值不同的两个序列的互相关函数值为0。这表明logistic序列具有遍历性,且其产生序列的概率密度分布函数与初值无关。因此,设定适当λ值、并取两个不同x值作为初值,可得到两个互不相关的混沌序列。通常可对生成的混沌序列进行二值量化处理,量化处理所用的阈值函数如下所示
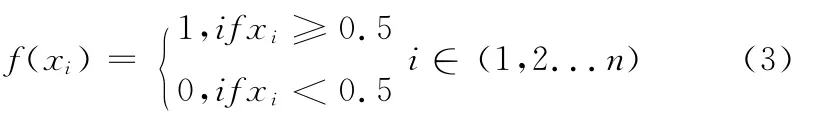
式中:xi——生成的混沌序列中第i个元素值,f (xi)——其量化后的对应值。
根据上述混沌映射特性,可以快速得到随机性很强的混沌序列。本文的加密算法通过设定初值作为密钥产生logistic混沌序列,对该混沌序列进行量化处理后得到二值混沌序列,然后利用该序列对图像进行第一次加密处理。由于混沌的初值敏感特性,初值的极小改变会导致产生完全不同的混沌序列,因而极大增强了系统的安全性。
2 触发细胞自动机
在细胞自动机中,有一类具有特殊性质的细胞自动机,其细胞单元的转换状态与其邻域状态配置中的某个单元的状态值之间存在线性关系,即改变邻域状态配置中这一单元的状态值将直接导致转移状态的改变,称这种转移状态与其邻域状态配置中的某位状态具有线性关系的规则为反转规则,这类细胞自动机称为触发细胞自动机 (toggle-CA,TCA)。TCA的迭代过程可描述为
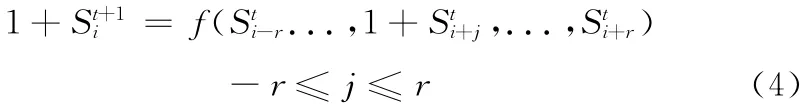

表1 规则90的反转规则
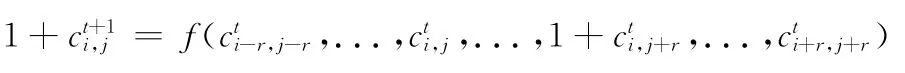
3 算法描述
根据上面说明的混沌产生方法和2D-TCA的原理,可设计基于混沌和细胞自动机的图像加密算法,以大小为M×N的灰度图像IM×N为加密对象,本文的加密算法可描述如下:
(1)设定迭代次数count=0,最大迭代次数countmax;
(2)设定混沌参数初值μ=μ0,λ=λ0,由式 (1)产生长度为M×N的混沌序列 {{Li}}并二值化处理,其中,0<i≤M×N;
(3)将混沌序列L与图像I进行异或运算,得到图像LIM×N;
(4)产生2D-TCA 反转规则f,以 LIM×N作为该2DTCA的初态;
(5)利用反转规则f依次对最左列的每个细胞进行迭代加密;
(6)2D-TCA每列循环左移一次;
(7)迭代次数count加1;
(8)若count<countmax,转第 (2)步;否则结束,得到加密图像LICA。
依照上述加密过程,可得到相应的解密过程,解密算法可描述如下:
(1)设定迭代次数count=0,最大迭代次数countmax;
(2)设定混沌参数初值μ=μ0,λ=λ0,由式 (1)产生长度为M×N的混沌序列 {Li},其中,0<i≤M×N;
(3)2D-TCA循环右移一次;
(4)产生2D-TCA反转规则f,以LICA作为该2DTCA的初态;
(5)按照反转规则f依次对最左列的每个细胞进行解密;
(6)用混沌序列L与图像I进行异或运算;
(7)迭代次数count加1;
(8)若count<countmax,转至第 (2)步;否则结束,即得到解密图像。
从上述算法描述可以看出,加密和解密互为逆过程,其不同之处在于加密和解密循环移位的方向相反;移位和异或运算的顺序相反。因此在硬件实现时,加解密功能可实现模块共享。其硬件系统只需由一个双向移位寄存器、一个移位寄存器控制单元、一个反转规则生成器、一个异或运算单元及一个混沌序列生成器构成,因此很容易进行硬件实现。
4 仿真实验与分析
4.1 密钥空间分析
加解密过程中,密钥由混沌初值μ,λ和细胞自动机的规则共同决定。半径为r的2D-TCA系统有24r+1种细胞配置状态,有224r+1种规则,该算法的密钥空间随着r的增加呈现指数及增长。即使取半径r为1,由μ,λ的取值范围可知密钥空间仍然足够大,采取穷举搜索是无法得到密钥的,即该加密系统是计算安全的。
4.2 算法效率分析
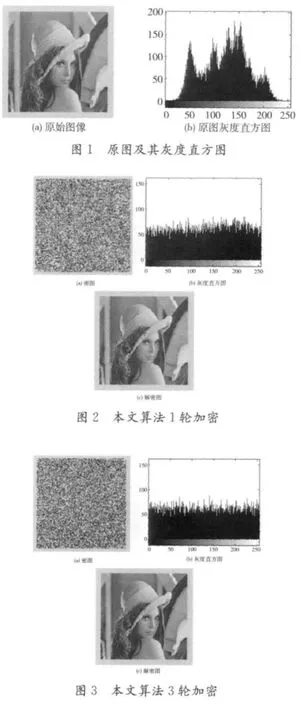
本文对上述算法进行了仿真实验。实验所用的原图像为128×128的8位灰度图,如图1(a)所示,图1(b)为原图像的灰度直方图。实验中的参数设定分别为:logistic混沌系统初值μ=4,λ=0.6,触发细胞自动机邻域半径r=1,构造的反转规则用二进制表示为 (01100101011001010110010101010110)。
为了说明算法的效率,实验对一般细胞自动机迭代加密方法和本文的算法进行了加解密的比较实验。图2、图3、图4分别为本文算法1轮、3轮、5轮迭代的加密结果、密图直方图和解密图像。用一般细胞自动机迭代方法经过6轮迭代后也可得到较好的加密效果,其密图、密图直方图和解密图像如图5所示。但与之相比,本文算法只需3轮迭代已经可得到较好的加密结果,因此具有较高的效率。
4.3 密钥敏感性分析
本文算法的密钥由混沌系统初值和细胞自动机规则共同确定。由于混沌系统的初值敏感特性,初值的微小改变将导致无法得到正确的解密图像。实验中分别设定加解密时的初值λ0为0.6和0.6+10-6,得到的加密结果如图6(a)所示,图6(b)为错误解密图像。结果表明,即使对于10-6这样微小的改变,得到的解密图像是完全错误的,这说明该加密系统对密钥的变化非常敏感。

一个好的加密系统必须满足 “雪崩”效应,即任意改变明文、密文或密钥的一位后,其误差传播应该使得相应的密(明)文产生明显变化。图7(a)、图7(b)分别表示5次迭代加密后,明文 (密文)改变一位所引起的对应的密文 (明文)的扩散变化情况。实验表明,明文 (密文)的微小变化会引起 “雪崩效应”,从而可以有效抵抗差分分析攻击。
4.4 相邻像素相关性分析
原始图像中相邻像素通常具有很大的相关性。相邻像素的相关性可反应出图像像素的扩散程度。
相关性越小,随机性越好,即加密性能越好,此时攻击者是无法通过像素的相关性来破解密图的。性能良好的加密系统应尽量让密图的相邻像素相关性系数接近零。图8、图9、图10分别反映了原图和密图的水平方向、垂直方向、对角线方向的相邻像素相关性情况。不难看出,原图不论在哪个方向上的相邻像素之间都具有很高的相关性;而密图中,各方向上相邻像素的相关性呈现出高度的随机分布特性,说明此时相邻像素的相关性已经几乎为零。

图7 密文 (明文扩散情况)
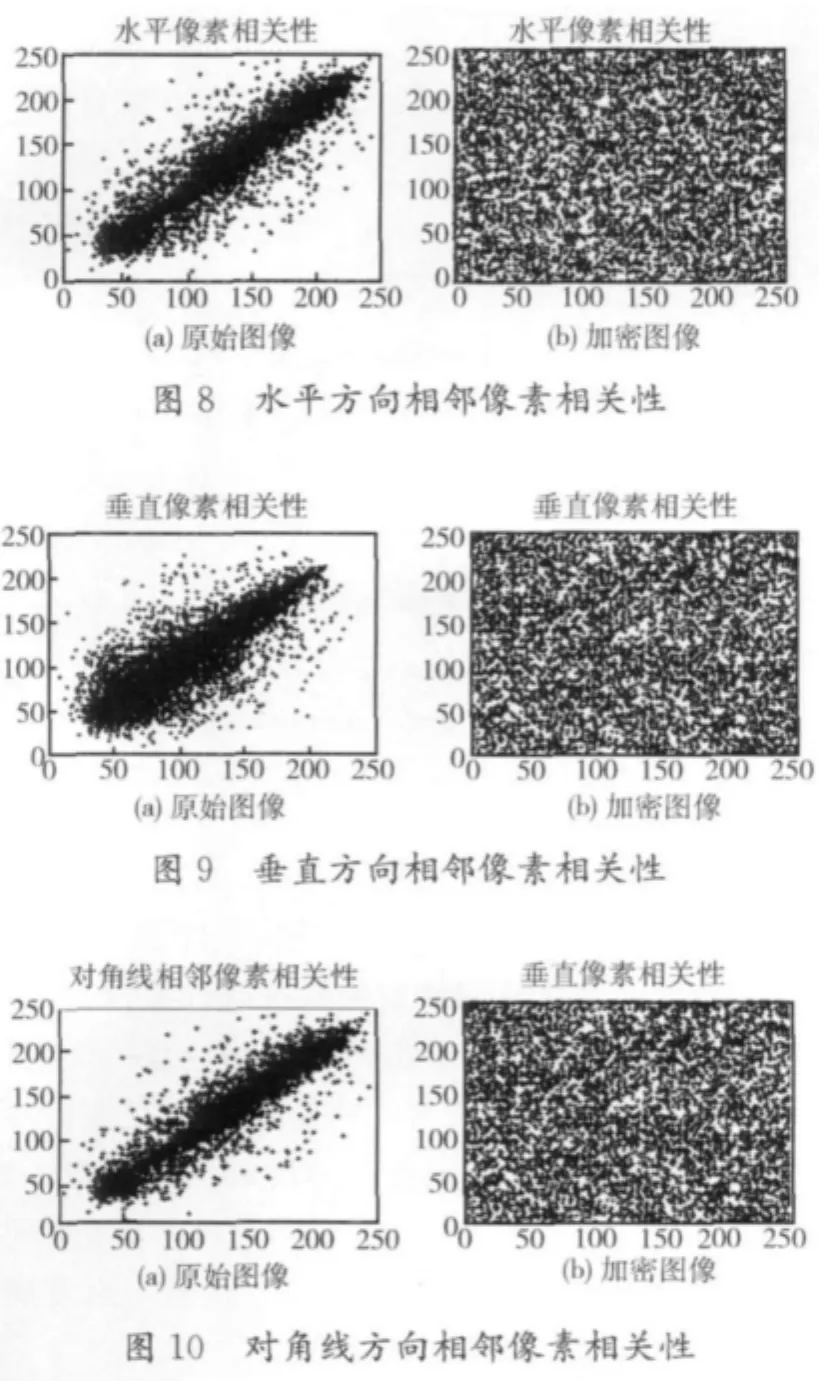
表2说明了原图、密图各方向上相邻像素的相关性系数。可以看到,原图的相邻像素具有很高的相关系数值,而加密后的图像相邻像素相关系数接近于零,即其相邻像素已基本不相关,说明本文的加密算法具有较好的扩散效果。
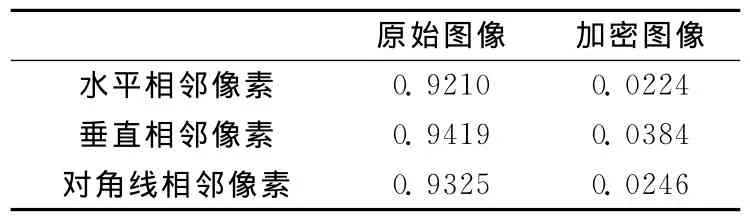
表2 相邻像素相关性系数
5 结束语
混沌系统具有良好的加密性能,但低维混沌系统如logistic混沌系统的密钥空间较小,缺乏足够的安全性;细胞自动机迭代加密方法简单易行,但较大的邻域半径不利于硬件实现。本文提出的基于混沌和细胞自动机的图像加密算法,结合了两者的优点,实现了一种简单可行,且便于硬件实现的图像加密算法。由于密钥由混沌初值和细胞自动机迭代规则共同确定,所以具有很大的密钥空间。在细胞自动机的邻域半径较小时,也可得到很好的加密效果,所以非常便于硬件实现。可在此基础上实现一种高性能、低代价的硬件加密系统。
[1]ZHANG Chuan-wu,SHEN Ye-qiao,PENG Qi-cong.Encryption based on cellular automata inverse iteration [J].Chinese Journal of Computers,2004,27 (1):125-129.
[2]Seredyn ski F,Bouvry P,Zomaya A Y.Cellular automata computations and secret key cryptography [J].Parallel Computing,2004,30 (5):753-766.
[3]Marcin Seredynski,Pascal Bouvry.Block encryption using reversible cellular automata [J].New Generation Computing,2005,23 (9):245-258.
[4]Sung J,Hong D,Hong S.Cryptanalysis of an involutional block cipher using cellular automata [J].Information Processing Letters,2007,104 (5):183-185.
[5]Tan S K,Guan S-U.Evolving cellular automata to generate nonlinear sequences with desirable properties [J].Applied Soft Computing,2007,7 (3):1131-1134.
[6]Jin Jun.Image encryption method based on elementary cellular automata[C].Proc of IEEE SOUTHEASTCON.Tatlanta,USA:IEEE Press,2009.
[7]ZHANG Xiaoyan,WANG Chao,LI Sumei,et al.Image encryption technology on two dimensional cellular automata [J].Journal of Optoelectronics Laser,2008,19 (2):242-245 (in Chinese).[张晓岩,王超,李素梅,等.基于二维细胞自动机的图像加密技术 [J].光电子·激光,2008,19 (2):242-245.]
[8]XIA Xuewen,LI Yuanxiang,ZHU Jixiang.A high-quality pseudorandom numbers generator based on two-layer couple cellular automata [C].Proceedings of the Eleventh Conference on Congress on Evolutionary Computation,2009:2265-2272.
[9]XIA Xue-wen,XIONG Zeng-gang,LI Yuan-xiang.Data encryption based on multi-granularity reversible cellular automata[J].Computer Engineering and Design,2010,31 (16):3599-3603(in Chinese).[夏学文,熊曾刚,李元香.多粒度可逆细胞自动机模型的数据加密方法 [J].计算机工程与设计,2010,31 (16):3599-3603.]
[10]XIA Xue-wen,LI Yuan-xiang,ZENG Hui.Data encryption algorithm based on two dimension toggle cellular automata[J].Computer Science,2010,37 (3):46-48 (in Chinese).[夏学文,李元香,曾辉.二维可反向迭代细胞自动机在数据加密中的应用 [J].计算机科学,2010,37 (3):46-48.]
