一种模态弱响应且模态密集的参数识别方法

贾天娇 岳 林

南京航空航天大学，南京，210016

0 引言

传统的实验模态分析方法已经在航空航天、建筑、运输、机械、能源等几乎所有与结构动态分析有关的领域中得到了广泛而成功的应用［1］，该类方法要求同时测得结构上的激励和响应信号。而运行模态分析仅根据系统的响应进行结构的模态参数辨识，不需施加人工激励，试验简便且不受结构形状和大小的限制，不影响结构的正常工作，同时也避免了对结构产生损伤，安全性好。因此，运行模态分析比传统的实验模态分析方法更具有优越性，更适合工程实际应用中一些大型结构（如桥梁、高层建筑以及海洋平台等）或特殊系统（如运转的转子系统、运行中的飞行器等）的测试和分析。

运行模态系统参数识别的数据非平稳，含有大噪声，为宽带随机激励且输出信号较弱，对于高柔度的飞机或桥梁以及输油管线结构，一般还存有密集模态。目前，在假设结构为线性系统的基础上，运行模态辨识的方法很多，但对弱响应输出且固有频率非常密集的结构的识别效果往往不尽人意。2004年，LMS公司推出PolyMax法［2］，即多参 考 最 小 二 乘 复 频 域 （least squares complex frequency，LSCF）法，该方法对小阻尼密集模态系统的参数采用稳定图法进行多次识别，有较好的精度。此外，小波分析方法在非平稳响应参数识别方面，有很好的去除噪声、获取系统主要模态频率的效果，对短样本、大噪声和密频数据的模态识别效果良好［3－6］。实际测量过程中获得的响应信号的各阶特征能量往往相差悬殊，在利用响应信号的相关函数［7－8］进行振动结构模态参数识别时，由于相关函数使大能量信号增强，小能量信号减弱［9］，已有的PolyMax法和小波模态辨识法，无法有效地对能量极小的弱响应模态特征进行辨识。为了解决此问题，本文先通过传递率的计算来突出弱响应信号的频率特征，然后针对大噪声、密频的特点再采用小波模态辨识法识别模态频率和阻尼比。

1 联合方法的理论

1.1 传递率的概念

当激励力为近似平稳白噪声时，系统的激励力为f（t），设每个测点i输出的响应信号为xi（t），i＝1，2，…，n。对一个测点j，系统频响函数的H1估计为

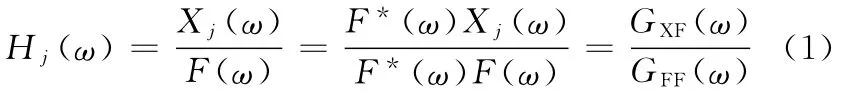
式中，F（ω）、Xj（ω）分别为激励力f（t）和输出xi（t）的傅里叶变换；GFF（ω）为激励力f（t）的自功率谱密度；GXF（ω）为输出xi（t）和激励力f（t）的互功率谱密度。

对两个测点j和p（j≠p），系统的传递率定义为

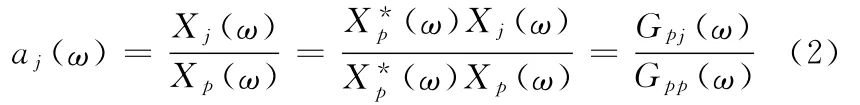
式中，Gpp（ω）为测点p响应的自功率谱密度；Gpj（ω）为测点p和测点j响应的互功率谱密度。

比较式（1）与式（2），可知传递率与频响函数的H1估计非常相似［10］，对传递率作傅里叶逆变换后，就可进行模态参数识别。一般情况下，应选取响应较大的测点为参考点，计算其他测点与该参考测点的传递率。

式（2）中，传递率以参考点p的自功率谱密度Gpp（ω）作为分母，当参考点p的特征频率ωr（r＝1，2，…，N，系统共有N阶固有频率）的能量越大时，自谱Gpp（ωr）的值也越大，而1/Gpp（ωr）的值越小，相对应的aj（ωr）减小，即此处的大能量信号削弱。同理，特征频率ωr的能量越小，aj（ωr）越大，即小能量信号更加突出。例如，两正弦信号x1和x2，取 采 样 点 数 4096，采 样 率 160Hz，x1＝100sin（40πt）＋0.1sin（60πt），x2＝ 80sin（40πt）＋sin（60πt），显然，信号x1和x2各自的2阶特征能量均相差悬殊，选信号x1作为参考，计算得到的信号x1和x2的互谱密度如图1所示。信号x1和x2的传递率的幅频特性如图2所示。

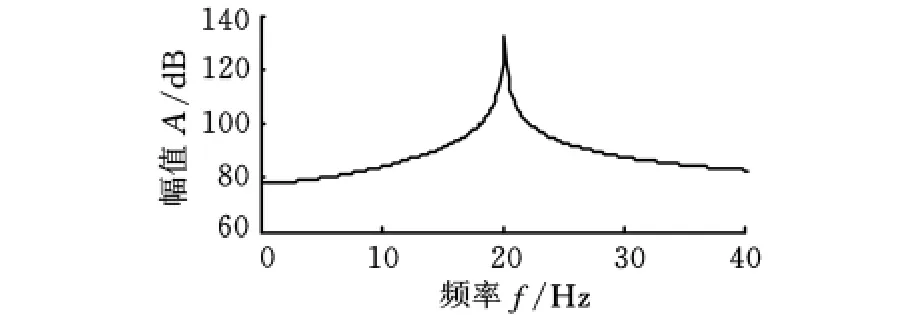
图1 信号x1和x2的互谱密度

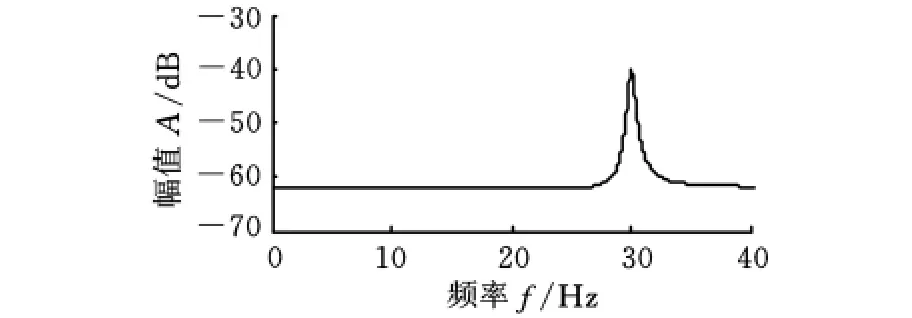
图2 信号x1和x2的传递率幅频特性

由图1、图2可知，信号间的相关函数导致30Hz的小能量特征被削弱，难以辨识；而信号间的传递率计算导致的20Hz的大能量特征相互抵消，同时使得30Hz的弱小特征更加突出。因而，传递率法对弱小模态特征的辨识具有很大的优势。

1.2 联合方法模态辨识原理

本文提出的联合相关函数和传递率的小波模态辨识方法（简称联合方法）的实现步骤如下：

（1）选择参考点。每次分析，选择一个输出作为参考后，再取一个输出，如（2）～（4）采用选定的两组输出信号进行系统模态辨识。

（2）计算相关函数和传递率。对大能量响应模态的辨识先计算相关函数，对弱响应模态的辨识则先计算传递率，使其更加突出后再用傅里叶逆变换求出传递率对应的时域信号。

（3）连续小波变换。针对数据短样本、大噪声、密频的特点，对相关函数和传递率对应的时域信号分别进行连续小波变换。

（4）模态参数辨识。根据小波系数与模态参数的关系［11］，对用小波系数脊提取法分离出的单一频率信号，通过小波骨架包络线的自然对数的斜率和小波骨架相位的斜率，识别出结构的模态参数。

（5）统计结果。重复（1）～（4），对所得模态辨识结果进行统计，得到完整的系统参数辨识结果。

联合方法模态辨识思路如图3所示。

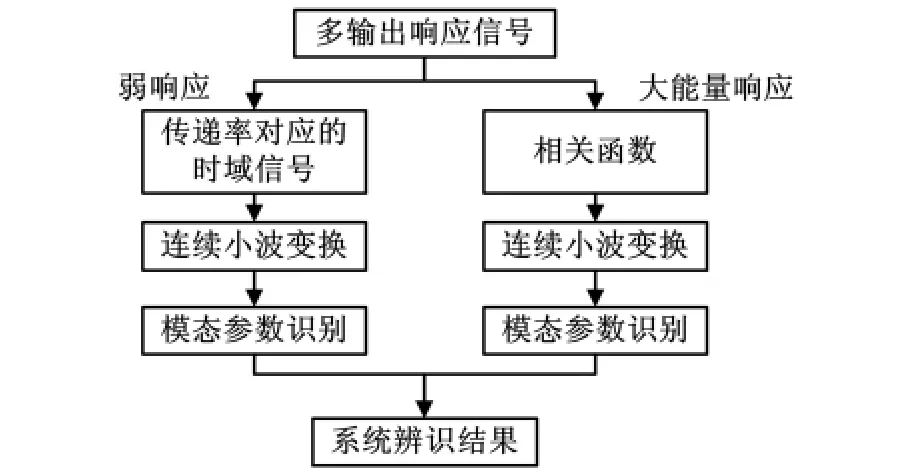
图3 联合方法模态辨识流程图

2 仿真实验

为了验证联合方法的有效性，采用GARTEUR飞机模型数据建立随机激励的数值仿真模型。GARTEUR飞机模型是欧洲航空科技研究集团于20世纪90年代设计的具有真实飞机高柔度密集模态的飞机模型，该模型真实地模拟了实际飞机的动态特性［12］，第3～5阶为密集模态，频率依次为33.01Hz、33.66Hz和35.14Hz，阻尼比均为1%。

GARTEUR模型在运行状态下，信号采样率为256Hz，采样点数为15360，共7个通道，其中通道2～7为不同测点的输出。各输出通道响应信号0～40Hz的傅里叶谱如图4所示。由图4可知，系统的第1阶特征的能量极大。图5所示为输出通道6的15～40Hz的响应信号傅里叶谱。由图5可知，第2阶及30～40Hz的3阶密集特征的能量极小、淹没在噪声中。因此，系统各阶特征的能量相差悬殊，要得到完整而精确的辨识结果有较大的难度。

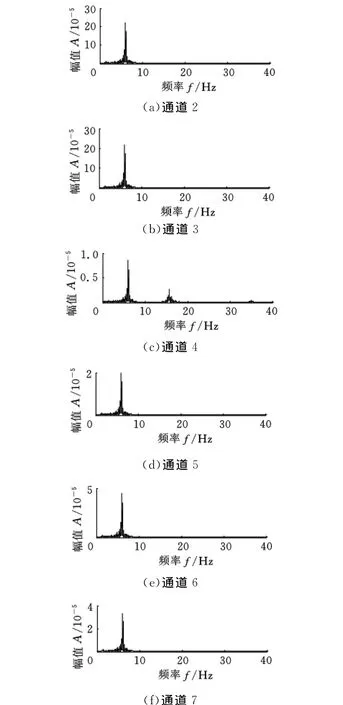
图4 各输出通道响应信号的傅里叶谱（0～40Hz）

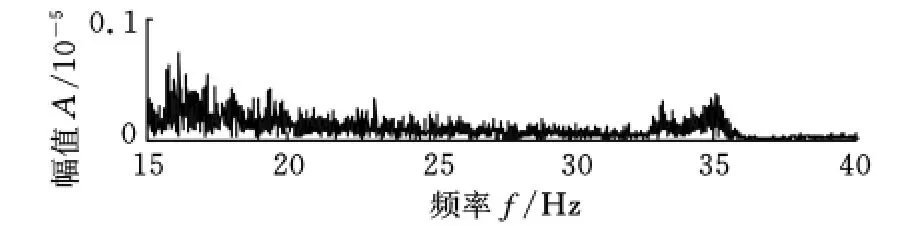
图5 通道6响应信号的傅里叶谱（15～40Hz）

下面将通道2作为参考，以通道6为例，具体说明本文提出的联合方法的模态辨识过程。首先，分别计算通道2和通道6间的互相关和传递率。互相关的傅里叶谱即互谱如图6所示，从其上仅能观察到能量极大的第1阶特征。而在图7所示的传递率幅频特性中，第1阶的大能量特征相互抵消，同时，第2阶及第3～5阶弱小特征都得到清晰地展现，使得此4阶模态易于辨识。显然，对于具有弱小特征的系统响应，使用响应信号的传递率，可增强信号，保证其可辨识性。

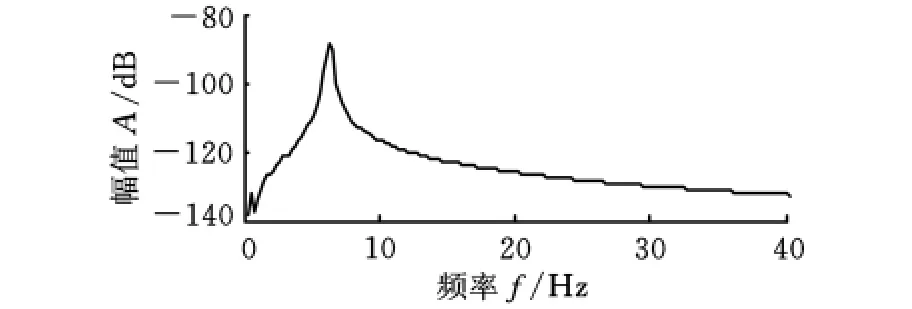
图6 通道2和通道6间的互谱

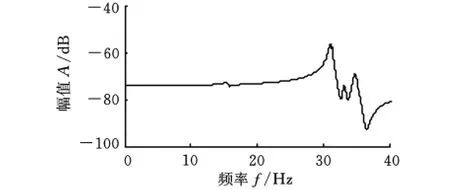
图7 通道2和通道6间传递率的幅频特性

其次，对互相关和传递率傅里叶逆变换信号分别进行连续小波变换，连续小波变换后的小波时频图及小波骨架如图8、图9所示。

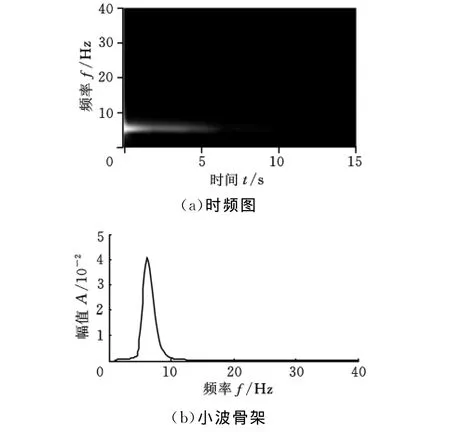
图8 互相关的时频图及小波骨架

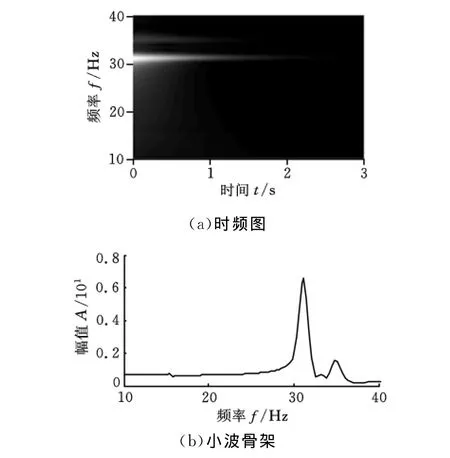
图9 传递率傅里叶逆变换信号的时频图及小波骨架

然后，由小波系数与模态参数的关系识别出结构的模态参数。图10所示为第1阶特征至第4阶弱小特征的小波模态识别的小波系数幅值拟合图和相位拟合图。

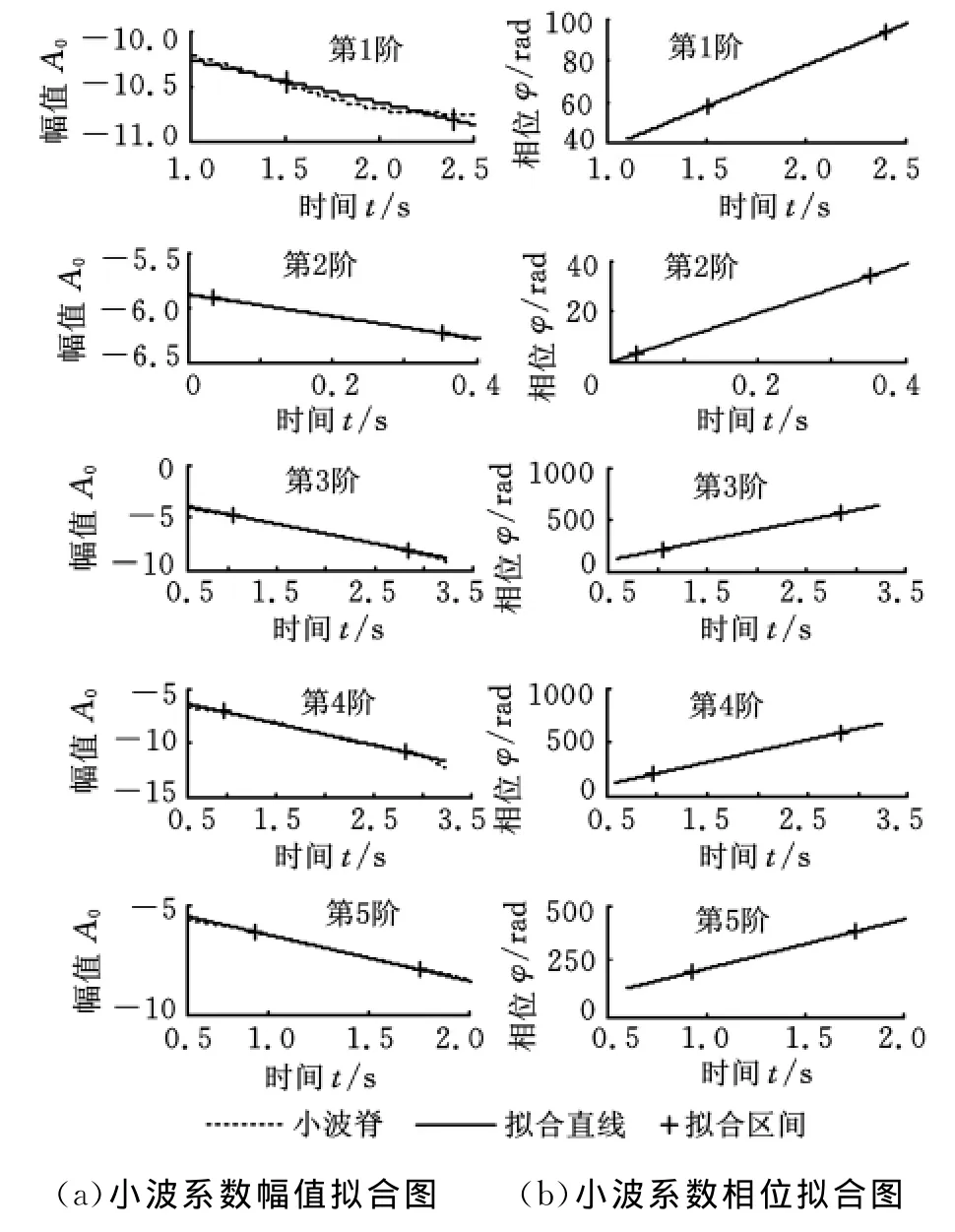
图10 GARTEUR模型的5阶模态识别的小波系数幅值拟合图和相位拟合图

为了对本文方法的仿真结果进行验证，采用LMS国际公司推出的 MACEC（modal analysis on civil engineering construction）系统识别商业软件［13］（3.1版本）进行识别，选择多参考最小二乘复频域法（pLSCF）的运行模态分析结果作为参考。pLSCF算法理论的总体思路与时域的最小二乘复指数法（LSCE）很相似，用于运行模态分析时，是以自谱、互谱矩阵为基础的。分析过程中，pLSCF法的自谱、互谱采用相关图法计算，即由相关函数间接求得，图11a所示为以通道2为参考，与通道6间的互谱，第1阶特征明显且其余4阶弱小特征无法观察到，同本文计算的互谱图6辨识效果一致；选择GARTEUR数据的6个输出通道为参考通道，相关函数计算时延为1024，最后计算的稳态结果如图11b所示，图11c所示为稳态图的局部效果图，从图中可以更清楚地观察30～40Hz间的3阶密集模态识别结果，其中⊕表示频率、阻尼和模态3种参数全部稳定，辨识结果可靠。

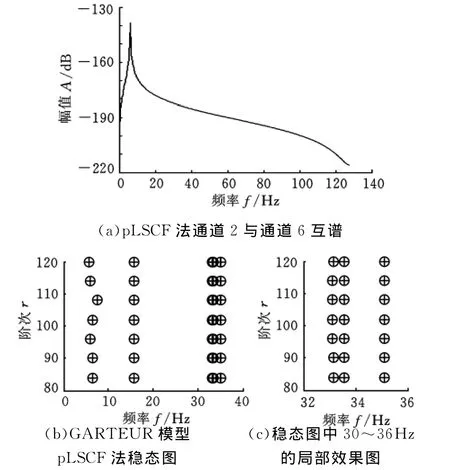
图11 基于最小二乘复频域法（pLSCF）计算的互谱和稳态图

表1所示为联合方法模态辨识统计结果与pLSCF法辨识结果对比。

由表1可知，PolyMax法在一般情况下的效果良好，但针对本文“响应信号数据样本较短、模态密集以及弱响应信号淹没在大噪声中”的情况，此方法的识别效果并不令人满意，因尽管其模态频率辨识精度较高，但其阻尼比的辨识结果却非常不理想。相比而言，本文提出的联合方法尽管模态频率辨识相对误差要比PolyMax法稍大，但总体来说其模态频率辨识精度还是较好的；另外，联合方法不仅极大地提高了阻尼比的辨识精度，而且还明显地改善了30～40Hz间的3阶模态密集的弱响应的模态识别效果。

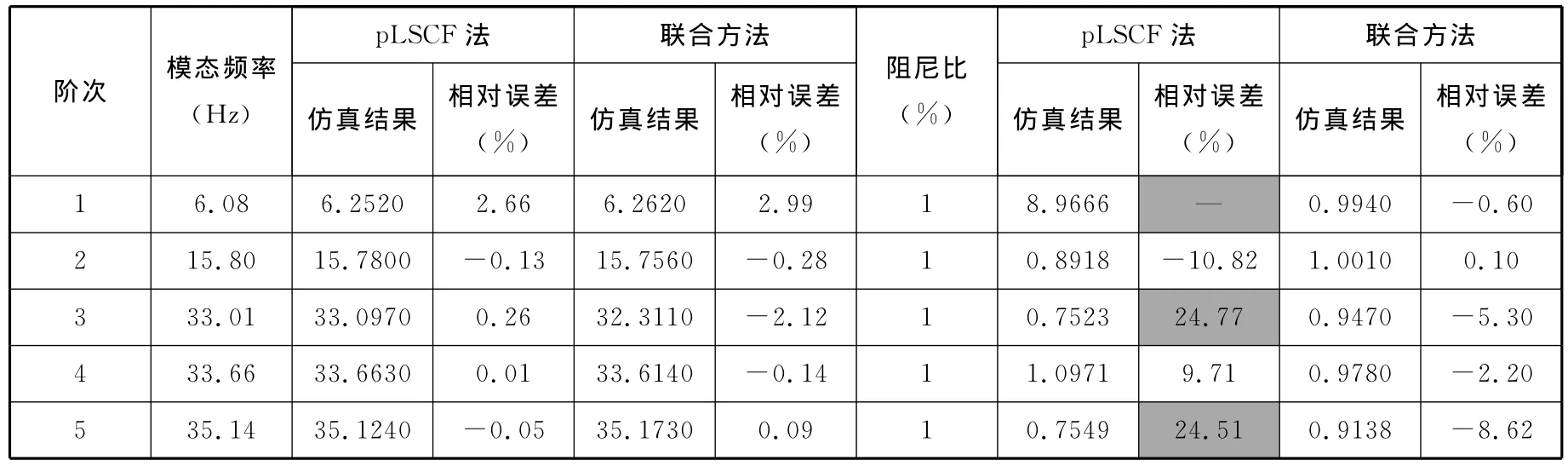
表1 GARTEUR模型在两种不同方法下的模态参数识别结果

3 结论

（1）响应信号间的相关函数会导致大能量信号的增强，但与此同时会导致小能量信号的削弱。因而，相关函数法模态参数识别适合于大能量信号的模态特征辨识，对弱响应模态的辨识难以奏效。

（2）响应信号间的传递率计算导致大能量信号相互抵消，同时使小能量信号更加突出。因而，传递率法模态参数识别无法辨识大能量信号的模态特征，但对密频、噪声淹没情况下的弱响应模态的辨识具有很大的优势。

（3）小波模态参数识别方法对短样本、大噪声、密频数据的模态识别效果良好。

（4）基于传递率和相关函数的小波模态参数识别方法即联合方法，仅通过输出的响应信号就可完整准确地辨识出大噪声下具有弱响应、密集模态特征系统的模态参数。

［1］Pintelon R，Guillaume P，Rolain Y.Parametric Identification of Transfer Functions in the Frequency Domain－a Survey［J］.IEEE Transacttons on Automatic Control，1994，39（11）：2245－2260.

［2］刘馥清，安宏伟.多参考最小二乘复频域（PolyMax）法在汽车轮胎及车身模态参数识别中的应用［C］//2006年LMS首届用户大会论文集.苏州：LMS国际公司，2006：1－7.

［3］Lardies J，Ta M N，Berthiller M.Modal Parameter Estimation Based on the Wavelet Transform of Output Data［J］.Archive of Applied Mechanic，2004，73（9/10）：718－733.

［4］徐亚兰，陈建军，胡太彬，等.系统模态参数辨识的小波变换方法［J］.西安电子科技大学学报（自然科学版），2004，31（2）：281－285.

［5］黄天立，楼梦麟.小波变换在密集模态结构参数识别中的应用［J］.振动与冲击，2006，25（5）：149－152.

［6］柳小勤，岳林，朱如鹏.连续小波变换应用于密集模态参数识别［J］.南京航空航天大学学报，2007，39（4）：496－499.

［7］James G H，Carne T G，Lauffer J P.The Natural Excitation Technique（NExT）for Modal Parameter Extraction from Operating Structures［J］.The International Journal of Analytical and Experimental Modal Analysis，1995，10（4）：260－277.

［8］孙晓兰，王太勇.基于相关函数的振动结构工作模态参数识别方法［J］.天津大学学报，2007，40（4）：503－506.

［9］樊江玲.基于输出响应的模态参数辨识方法研究［D］.上海：上海交通大学，2007.

［10］毛宽民，李斌.基于响应信号的结构模态参数提取方法［J］.华中科技大学学报（自然科学版），2008，36（7）：77－80.

［11］Yan B F，Miyamoto A，Brühwiler E.Wavelet Transform－based Modal Parameter Identification Considering Uncertainty［J］.Journal of Sound and Vibration，2006，291（1/2）：285－301.

［12］Balmes E.GARTEUR Group on Ground Vibration Testing－results from the Test of a Single Structure by 12Laboratories in Europe［C］//Proceedings of 15th IMAC.California：SEM，1997：1346－1352.

［13］De Roeck G，Peeter B.MACEC2.0－modal Analysis on Civil Engineering Constructions［R］.Belgium：Catholic University of Leuven，1999.