An Approximate Calculation Method for Lateral Trajectory Correction
2012-07-25WANGZhongyuan王中原LIXiaoyuan李小元CHANGSijiang常思江
WANG Zhong-yuan(王中原),LI Xiao-yuan(李小元),CHANG Si-jiang(常思江)
(1.School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China;2.System Institute,Navy Arming Academy,Beijing 100073,China)
Introduction
The concept of trajectory correction deals with the technology that can measure the flight parameters,e.g.velocity and position,of launched projectiles in real-time,compare them with the predetermined ones,and then determine the control information and realize the dispersion reduction.The trajectory correction projectile which can only adjust the longitudinal trajectory is called as one-dimensional trajectory correction projectile(ODTCP),while if the lateral trajectory can also be modulated,it is called as two-dimensional trajectory correction projectile(TDTCP).
The technology of one-dimensional trajectory correction for large caliber rotary stabilized projectiles is relatively easy because it only needs to change the drag force.It is easy to implement this technology in structure.At present,the research on the one-dimensional trajectory correction technology is relatively mature[1].
In order to obtain the force used to adjust the lateral trajectory for TDTCP,the projectile’s spin rate must be reduced if some rudders or impulse engines arranged around the projectile’s body are used,thus the complexity and cost will be increased.All of these factors limit the development of TDTCP.According to the theory of exterior ballistics,the large caliber spin-stabilized projectile has a systematic deviation at the end of trajectory,i.e.the ballistic drift.Usually,the ballistic drift is of several hundred meters order of magnitude which is much more than the lateral dispersion.If a damping disc,as shown in Fig.1,could be added except the one-dimensionalcorrection mechanism,e.g.the drag brake,so as to change the polar damping moment and correct the trajectory via changing the ballistic drift,the whole correction mechanism will be low-cost and easy to be implemented.Obviously,it provides a good way for the development of TDTCP.At present,the study on TDTCP in foreign countries have achieved considerable progresses[2-3]and entered the stage of engineering prototype.The corresponding study in our country is still in the stage of preliminary theoretical analysis[4-5].
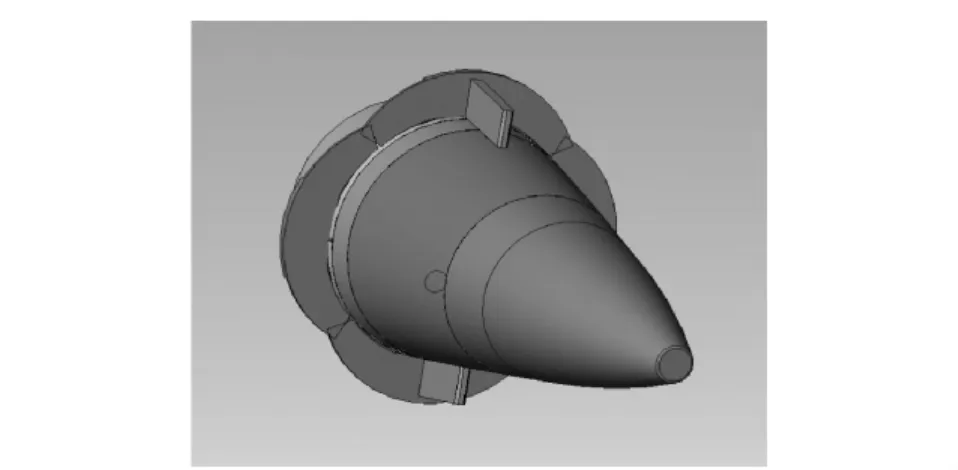
Fig.1 Sketch of projectile with two-dimensional trajectory correction
Following problems are extremely important for TDTCP.Generally speaking,the ability of correcting lateral trajectory for large caliber spin-stabilized projectile should be evaluated;the lateral correction should be calculated easily and quickly;the main factors affecting the correction ability should be analyzed;the flight stability criterion during the correction process should be established.This paper mainly discusses the above problems to lay a foundation for the research on TDTCP in the future.
1 Mathematical Model for TDTCP
The mathematical model of two-dimensional trajectory correction can be expressed as
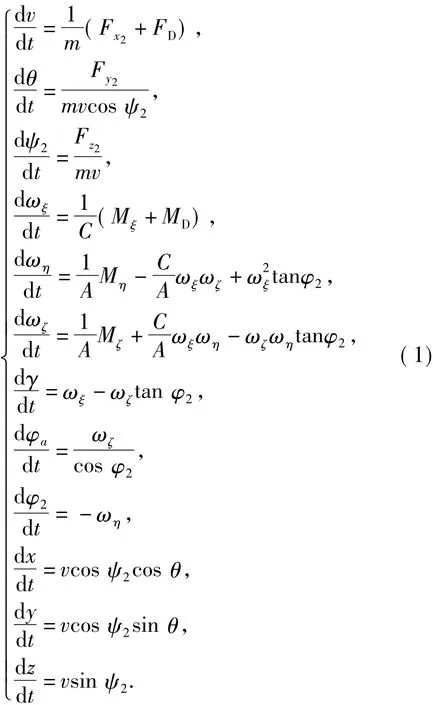
The governing equations are

whereFx,FyandFzare the projections of the resultant forceFon the trajectory coordinate systemC-x2y2z2,Mξ,MηandMζare the projections of the resultant momentMon the body-fixed coordinate systemC-ξηζ,FDandMDare the additional drag and rotational damping moment respectively,while the drag brake and disc are unfolded.The definitions of other symbols in the above equation can be found in literature[6].
From the trajectory model above,it is easy to know that the fixed positions,sizes and shapes of the unfolded drag brake and damping disc will directly affect the additive drag and polar damping moment for a specific spin-stabilized projectile,and therefore the effect of trajectory correction.Calculate the aerodynamic characteristics firstly for different drag brakes and damping discs,then calculate numerically by using the trajectory model given above,and finally analyze relative properties of two-dimensional trajectory correction and compare them with the approximate calculation formula deduced later in this paper.As this paper mainly analyzes the ability of correction,influencing factors and flight stability,the approximate calculation formula and a series of problems concerned with the lateral trajectory correction will be studied.
2 Approximate Calculations for Ballistic Drift and Trajectory Correction
According to the theory of exterior ballistics,the ballistic drift is caused by the yawΔpand mainly determined by its lateral componentδ2pwhich is normal to the perpendicular plane of fire direction.Projecting the acceleration to the ground coordinatesC-xyz,the lateral acceleration can be written as[6]
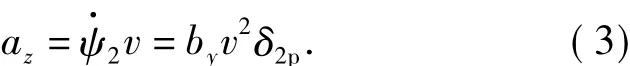
From Eq.(3),

where

Substituting the expressions above into Eq.(4)and integrating,
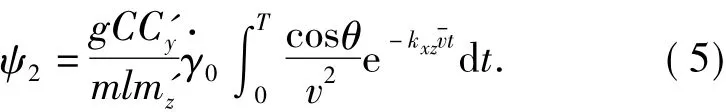
Considered the very small included angle between the tangent of trajectory at any point andx-axis,we have

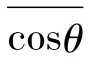
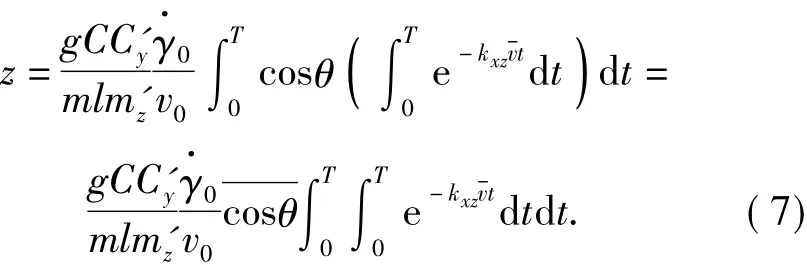
Integrating fromθ0toθcand averaging,
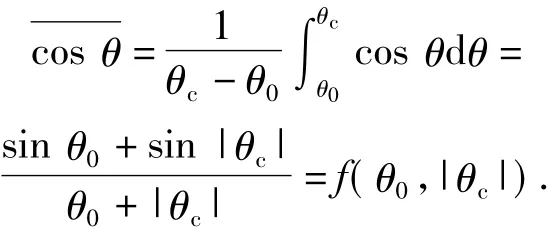
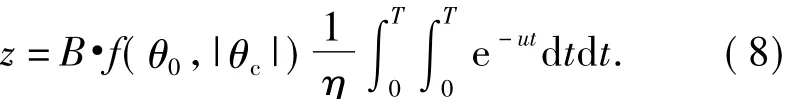
If there is no control in the whole flight,then the lateral ballistic drift at the fall point can be expressed as
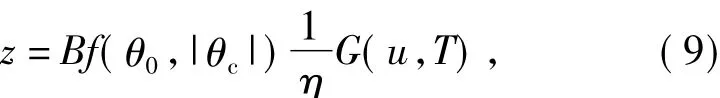
Assuming that the unfolded time of the damping disc on the spin-stabilized projectile with ability of lateral trajectory correction ist1,the corresponding polar damping moment ballistic coefficients arekxzandkxz1respectively,after integration,the lateral ballistic driftcan be written as
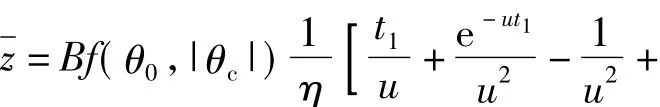
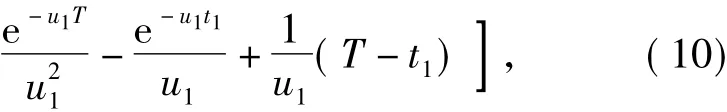
From Eq.(9)and(10),it is easy to know that,when the damping disc is unfolded att1,the approximate lateral correction corresponding to fall point is

From Eq.(9)and(11),it can be seen that:
1)Breflects the contribution of the projectile’s structure to the ballistic drift;
2)f(θ0,|θc|)reflects the influences of elevation angle on the ballistic drift.The larger the elevation angle is,the larger the ballistic drift and corresponding trajectory correction are;
3)1/ηreflects the influences of the gun twist on the ballistic drift.The smaller the twist is,the larger the ballistic drift and corresponding trajectory correction are;
4)G(u,T)reflects the influences of polar damping moment coefficient and time of flight on the ballistic drift.The smaller polar damping moment coefficient and the longer flight time correspond to the larger ballistic drift;
5) During the lateral trajectory correction process,the earlier the damping disc unfolds,the bigger the additional polar damping moment coefficient is,then the bigger the corresponding lateral correction generates.
According to the equations for the lateral trajectory correction at the fall point,it is easy to know that the bigger the damping disc is and the earlier it unfolds,the bigger the lateral correction is.However,it should also be noticed that the spin rate at the corresponding trajectory will be decreased quickly if the damping disc is designed too big or unfolded too earlier.In order to ensure that the projectile is still stable after the damping disc unfolded,the additive polar damping moment coefficient caused by the damping disc and the time that the unfolded damping disc lasts must satisfy a particular relationship to make the flight stable.This relationship corresponds to the situation under which the lateral ballistic correction is maximum.
According to the theory of exterior ballistics[7],the stability condition for spin-stabilized projectiles can be expressed as
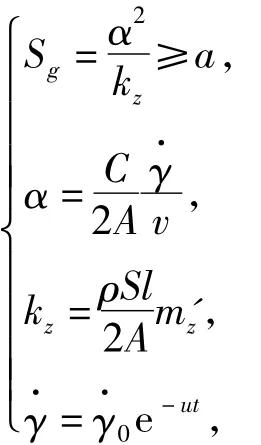
where the constanta>1.
When the damping disc unfolded att1,then the corresponding maximum lateral trajectory correction can be written as
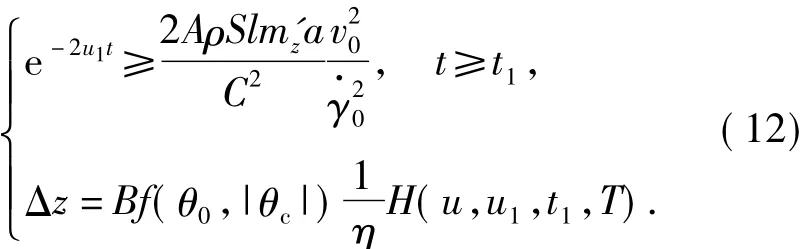
3 Numerical Example
According to the formulas for the ballistic drift and the lateral trajectory correction,based on the structure and ballistic parameters of a certain large caliber projectile,its correction ability can be calculated.The projectile’s massm=30 kg,lengthl=670 mm,rifle twistη=25.Set a damping disc with the unfolded height of 8 mm,axial length of 40 mm at the nose of the projectile.After calculation,when the damping disc unfolded,the projectile’s parameters arekxz=8.98 ×10-6,kxz1=2.25 × 10-5,the flight timeT=92.0 s;if the elevationθ0=45°,the lateral correction Δzwith the damping disc unfolding at different times is illustrated in Fig.2.
It can be seen from Fig.2 that,1)for a particular projectile and damping disc,the extent of spin rate reduction increases as the moment of opening the damping disc decreases,and the increase of the lateral correction is obvious,thus the correction capability is promoted;2)the correspondence between the calculation results and the numerical results by using the 6D trajectory model is better.Especially,the later the damping disc is unfolded,the higher the calculation accuracy of the approximate formula is.
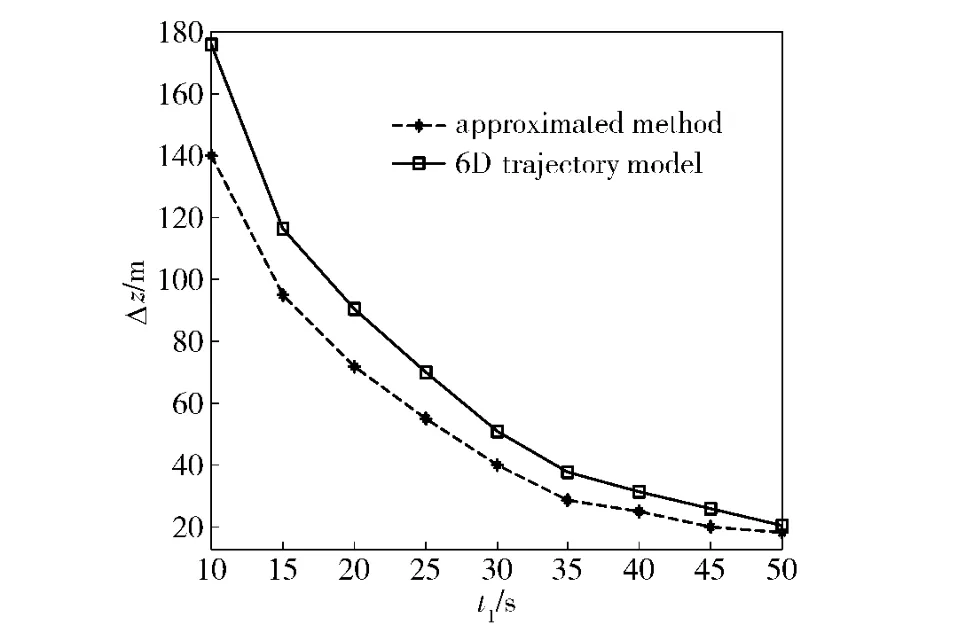
Fig.2 Horizontal correction vs.opening damping disc on different positions of trajectory
It is worth noticed that the damping disc decreases the ballistic drift with the cost of sacrificing the gyroscopic stability for the spin-stabilized projectile.However,the projectile must be flight stable during the whole process of correction.In order to keep the stability,the momentt1must meet the restraint Eq.(12).
4 Conclusions
It is a low cost method for large caliber spin-stabilized projectiles to realize two-dimensional trajectory correction by using the onboard drag brake and damping disc.Moreover,the rapid calculation and analysis of correction ability are the very important foundations for the trajectory correction technology.In this paper,based on the domestic achievements of ODTCP,the mathematical model of two-dimensional trajectory corrections is discussed;an approximate formula for predicting the ballistic drift and trajectory correction is deduced.The correction ability and the flight stability of TDTCP are also analyzed.All the work is valuable for further research.
[1]WANG Zhong-yuan,SHI Jin-guang.Aerodynamic structure and correctional ability for one dimensional trajectory correction projectile[J].Journal of Nanjing University of Science and Technology:Natural Science,2008,32(3):333-336.(in Chinese)
[2]Grignon C,Cayzac R,Heddadj S.Improvement of artillery projectile accuracy[C]∥Proceedings of the 23rd International Symposium on Ballistics,Tarragona:IBC,2007:747-754.
[3]Pettersson T,Buretta R,Cook D.Aerodynamics and flight stability for a course corrected artillery round[C]∥Proceedings of the 23rd International Symposium on Ballistics,Madrid:Graficas Couche,2007:647 -654.
[4]SHI Jin-guang,WANG Zhong-yuan,CHANG Si-jiang,et al.Technology of lateral trajectory correction based on spin velocity reduction control[J].Journal of Ballistics,2010,22(3):81-85.(in Chinese)
[5]HUO Peng-fei,YANG Xiao-hui,LIU Chuang.Deflection error correction method for spin stabilized projectiles based on despining approach[J].Journal of Detection and Control,2008,30(6):12-16.(in Chinese)
[6]XU Ming-you.Exterior ballistics of rocket projectiles[M].Harbin:Harbin Institute of Technology Press,2004.(in Chinese)
[7]PU Fa.Exterior ballistics[M].Beijing:National Defense Industry Press,1980.(in Chinese)
猜你喜欢
杂志排行
Defence Technology的其它文章
- Fault Diagnosis Method Based on Fractal Theory and Its Application in Wind Power Systems
- Numerical Simulation of Particle/Matrix Interface Failure in Composite Propellant
- Torque Ripple Suppression Control Strategy for Brushless Integrated Starter/Generator Wound-Field Synchronous Motor
- Monitoring Method for the Electrical Properties of Piezoelectric Transducer
- Molecular Dynamic Simulation for HMX/NTO Supramolecular Explosive
- Research on Microcrack Extension Mechanism of SiCp/Al in the Machining Process
