稳定配置与市场设计：合作博弈理论的扩展与应用——2012年度诺贝尔经济学奖得主夏普利和罗思主要经济理论贡献述评

李宝良，郭其友

（1.华侨大学 经济与金融学院，福建 泉州362021；2.厦门大学 经济学院，福建 厦门361005）

一、引 言

社会经济活动总是在冲突与合作中发展，资源相对于需求的稀缺性会导致竞争乃至引发冲突，但为了更好地利用稀缺的资源，人们有时也会相互合作。不言而喻，冲突有可能造成资源配置低效和福利损失，更严重的情况是导致人类社会深陷困境；而合作则能实现资源的更有效配置，从而提高人类福利。因此，如何构建运行有序、治理良好的社会经济制度以解决稀缺资源配置中的冲突与合作问题，就成为经济理论研究的一个重要课题。从某种意义上说，不管是亚当·斯密、约翰·斯图亚特·穆勒等古典经济学家，还是哈耶克、科斯、布坎南、诺斯、奥曼、谢林、威廉姆森和奥斯特罗姆等现代诺贝尔经济学奖得主，都曾孜孜以求地探寻各种旨在解决利益冲突以避免人类社会陷入困境，以及促进相互合作以提高人类福利的社会经济制度（Bowles，2006）。

传统的经济理论研究了以价格为中心的市场机制和制度在配置资源中的作用，证明了在满足特定条件的情况下竞争性市场机制能够调解各方的利益冲突，并使社会福利最大化。然而，现实经济生活中会出现很多价格机制因受到这样或那样的限制而不能很好发挥资源配置功能的情形。例如，很多公立学校不能向学生收取学费，器官移植因受到伦理道德的约束而不能进行单方面的转移支付，等等。于是，在价格机制不能发挥作用的情况下如何实现有效的资源配置，就成为经济理论研究所关注的课题。

本年度诺贝尔经济学奖获得者所研究的正是在价格机制不能发挥作用的情况下如何配置资源的问题。他们针对匹配市场（matching market）设计出了能使经济参与人更好、更有效率地实现资源配置的匹配算法或程序，解释了资源配置的性质等问题。由于解决这类问题需要考虑相互作用的交易双方如何合作或者结盟以更好地实现双方的福利，因此属于合作博弈理论的研究范畴。正如瑞典皇家科学院所言，夏普利引领了合作博弈论的发展，不仅夯实了合作博弈论的理论基础，而且还提高了合作博弈论在应用研究和政策制定方面的实用性。他与他的合作者（Gale）于1962年发表的《大学录取与婚姻稳定性》一文，在合作博弈论框架下提出了Gale－Sharpley算法，奠定了稳定配置研究的理论基础。20年以后，罗思将稳定配置理论运用于美国医生劳动力市场研究，并且发现全美住院医生匹配计划（National Resident Matching Program，NRMP）与 Gale－Sharpley算法不谋而合。Gale－Sharpley算法在实践中的应用又进一步推动了理论研究的发展。总之，他们通过理论研究、实证分析、实验研究加深了我们对市场运行机制的理解，直接推动了对现实世界中许多重要市场的重新设计。

二、夏普利和罗思生平及其贡献概述

夏普利是继约翰·冯·诺依曼（John von Neuman）和奥斯卡·摩根斯坦（Oskar Morgenstern）之后的合作博弈理论研究关键人物。他出生于1923年，是美国著名的数学家和经济学家，加州大学洛杉矶分校荣誉退休教授。夏普利的经历充满传奇，他于1943年就读于哈佛大学，同年作为中士参加美国陆军航空部队，前往中国成都支援抗日战争，期间因破解前苏联气象密码而获得铜质勋章。“二战”结束后，他回哈佛大学继续自己的学业，并取得了数学学士学位。而后，夏普利在兰德公司工作了一年，后又回学校继续深造，并在普林斯顿大学取得了博士学位。值得一提的是，夏普利值和博弈论中核（core）的概念，正是夏普利博士论文和博士后研究的主题。毕业后，夏普利于1954年回兰德公司工作，从1981年起在加州大学洛杉矶分校任教直到退休。

夏普利对经济理论和博弈理论的发展做出了奠基性的贡献，概括起来主要涉及两个方面。首先是扩展了合作博弈理论研究。他把“核”这个合作博弈一般解的概念引入合作博弈研究。现在，“核”已经成为合作博弈论的核心概念之一，可能也是经济学中最常用的合作解概念。“核”的引入为竞争性均衡提供了另一种重要的解释，并且使经济学家相信博弈论是分析经济问题的重要工具。其次是在合作博弈分析框架的基础上提出了公平分配的夏普利值公式以及稳定配置理论及其算法。现在，夏普利值已经成为研究公平分配问题最常用的工具，夏普利值及其变体在利益分配和成本分摊等方面得到了广泛的应用。夏普利提出的稳定配置理论为匹配市场的资源配置问题研究奠定了理论基础，他还提出了双边市场的Gale－Sharpley算法和单边市场的顶端交易循环算法（top－trading cycle algorithm），并证明了这些算法的稳定性和存在性等性质。这些算法及其变体为匹配市场制度设计提供了重要的理论依据。

夏普利因其卓越的经济理论贡献而获得过许多荣誉。他是美国计量经济学协会会员、美国艺术和科学研究院院士、美国国家科学研究院院士、耶路撒冷希伯来大学名誉博士等等，2007年被美国经济学协会评为杰出研究员。他还获得过许多奖励，其中最重要的是1981年获得的约翰·冯·诺依曼理论奖。该奖由美国运筹学和管理科学研究院每年颁发一次，旨在奖励对运筹学理论和管理科学研究做出过奠基性和持续性贡献的个人或团体。

罗思生于1951年，现是美国杰出的经济学家，哈佛大学商学院经济学与工商管理学乔治·冈德讲席教授，斯坦福大学客座教授。罗思1971年毕业于哥伦比亚大学，获得运筹学学士学位后又就读于斯坦福大学，并于1973年和1974年先后获得运筹学硕士和博士学位。毕业后，罗思先后执教于伊利诺伊大学和匹兹堡大学。1982年，罗思担任匹兹堡大学安德鲁－梅隆经济学讲席教授、匹兹堡大学科学哲学研究中心研究员以及卡兹商学院教授。1998年，罗思离开匹兹堡大学到哈佛大学任教，2012年又回到斯坦福大学工作并将于明年成为该校全职教员，同时一直保留着哈佛大学荣誉退休教授的待遇。

罗思在博弈论、市场设计与实验经济学等领域的研究中做出了重大的贡献，并以强调运用经济理论来解决现实问题的重要性而闻名。可以说，罗思对经济理论的贡献都是围绕市场设计做出的。1984年，罗思研究了NRMP，并且发现NRMP能够实现未婚住院医生的稳定匹配，且能抵制他们的策略性行为，但无法实现已婚医生夫妇的稳定匹配（夫妻二人都是医生，把他们分开会导致不稳定的匹配）。1999年，罗思重新设计了这项匹配计划，从而使得即使是已婚医生夫妇也能实现稳定的匹配。此后，罗思帮助设计了纽约市公立学校匹配系统（New York City Public School Matching System）、波士顿公立学校匹配系统（Boston’s Public School Matching System）以及新英格兰肾脏移植计划（New England Program for Kidney Exchange）。随着新经济的发展，罗思的市场设计研究兴趣扩展到了电子商务网络拍卖等领域。

罗思对市场设计的兴趣反过来推动了他对经济理论的研究。首先，要解决原有匹配程序所存在的问题以及根据不同匹配市场的特点重新设计匹配系统，就必须从理论上分析相关的经济性质，再根据经济环境和伦理道德约束来改进原有的算法或程序，从而促使罗思对博弈论进行深入的研究。其次，在进行市场设计或重新设计时，罗思广泛采用不同的实验经济学和计算经济学研究方法作为补充。实际上，罗思也是实验经济学领域的重要研究人员，他在实验经济学方面的贡献主要体现在他于1987年发表的《实验经济学：六种观点》和1995年与卡格尔（Kagel）合编的《实验经济学手册》这两本书中。前者收录了在实验经济学领域做出过重要贡献的主要研究人员的研究成果，介绍了他们在实验研究中积累的经验教训，阐述了他们关于实验方式、实验技巧和有利于理解经济行为的实验领域等方面的观点和看法，因而是实验经济学研究的重要参考文献。

与夏普利一样，罗思也因对经济理论和市场设计做出了重大贡献而获得过很多荣誉和奖励。他是古根海默（Guggenheim）学会会员、美国艺术与科学院院士、美国国家经济研究局（NBER）研究员、阿尔弗雷德·P·斯隆（Aftred P.Sloan）基金会和计量经济学协会会员；1980年获得得克萨斯方法基金奠基奖，1991年获得美国运筹学研究协会颁发的兰彻斯特（Lanchester）奖，2012年被美国器官移植代表大会授予医疗创新奖。

三、稳定配置和市场设计：合作博弈理论的扩展及应用

夏普利在扩展合作博弈论的基础上，又把合作博弈论应用于匹配市场研究，提出了稳定配置理论及其算法；而罗思则进一步扩展了稳定配置理论，并把它应用于现实中的市场设计。为更好地理解夏普利和罗思在稳定配置理论和市场设计研究方面所做出的杰出贡献，有必要简要概述合作博弈论的基本分析框架①。

（一）合作博弈论的基本分析框架

1944年，数学家冯·诺伊曼和经济学家摩根斯坦合作出版了《博弈论与经济行为》一书，标志着经济博弈论的创立。他俩根据经济参与人的典型行为特征提出了策略型与广义型（扩展型）基本博弈模型、解的概念和分析方法，同时还讨论了二人零和博弈，深入探讨了合作博弈问题，并且提出了特征函数形式的博弈模型。可以说，他俩奠定了非合作博弈和合作博弈理论大厦的基础。

一般地，非合作博弈是指参与人都独立行动、不存在有约束力的合作或联盟情况下的博弈，这种博弈强调的是个体理性，其结果可能是有效率或者无效率；而合作博弈是指在某些参与人之间存在有约束力的合作或联盟情况下的博弈，这种博弈强调的是集体理性，追求的是效率、公正和公平。男女婚配、学生和学校的双向选择以及肾脏等器官移植配对，都可以被看作是参与人合作结盟，旨在追求联盟总体效用最大化，因而非常适合用合作博弈（或联盟博弈，coalitional game）来进行分析。

根据收益能否转移，合作博弈可以进一步分为收益可转移联盟博弈（coalitional game with transferable payoff）和收益不可转移联盟博弈（coalitional game with non－transferable payoff）两类。收益可转移联盟博弈假设参与人都用相同的尺度来衡量他们可赢得的收益，且联盟可赢得的收益可按任意方式在联盟成员之间分配。简单地说，效用就像货币一样，可以在参与人之间自由转移，否则就是收益不可转移联盟博弈。

用数学公式，合作博弈可以表示为一种特征函数形式的博弈｛N，v（S）｝，这里 N＝｛1，2，…，n｝，表示由n个参与人组成的集合，N的任何非空子集S表示一个联盟，按照排列组合理论，可能存在的联盟有（2n－1）个②，其中由单个参与人｛i，i∈N｝构成的集合称为单人联盟，而包括全部参与人的集合N则称为统一战线联盟；v（）是N的任何非空子集S所构成的联盟的特征函数，v（S）表示联盟S可赢得的最大收益，联盟成员可以任何方式在成员之间转移或分配联盟赢得的收益v（S）。特征函数是合作博弈各种解的概念的基础。

合作博弈理论提出了一种在假设联盟内部潜在利益冲突可按有约束力的协议来解决的条件下导致参与人结盟的激励机制。定义x＝（x1，x2，…，xn）为收益向量，其中xi表示参与人i的收益。当联盟S可以在配置x的基础上增加收益时就有，那么，配置x是不稳定的，因为此时i∈S联盟S的成员可以通过合作争取更大的收益v（S），并采用能使联盟所有成员的收益严格优于配置x下的收益的方式来分配所赢得的收益；相反，当）时，则称配置x是稳定的，所有i∈S稳定配置的集合构成合作博弈的核。

经济学中关于核的基本思想可以追溯到1881年埃奇沃斯提出的契约曲线这个概念。埃奇沃斯在引入契约曲线时推定：当市场主体充分多时，契约曲线大致等同于竞争性均衡曲线。他试图用埃奇沃斯方盒来证实在两个参与人、两种商品情况下的竞争性均衡问题。另外，核的思想暗含于1944年冯·诺依曼和摩根斯坦的稳定集解分析之中。20世纪50年代，夏普利先后发表了《N参与人博弈值》（Sharpley，1953）和《合作博弈市场》（Sharpley，1955）两篇论文，率先明确把核的概念作为合作博弈独立解的概念。1967年夏普利在《论平衡集与核》一文中推导出了稳定配置存在的条件，并且证明了在收益可转移联盟博弈中需要多大的联盟收益可供分配才能保证核不是空集。1971年，夏普利证明得出了凸博弈（convex game）的核总是非空的结论。同时，夏普利与其合作者舒彼克（Sharpley和Shubik，1959）证明了“契约曲线对应于经济中的核”的猜想。此后，Debreu和Scarf（1963）在更一般的条件下证实了这个猜想。从此，核概念成为竞争性均衡分析的关键性理论基础。

很多经济问题与完全竞争市场的基准有显著的不同，无法用竞争性均衡理论来进行分析。然而，值得庆幸的是，在这种情况下，仍然可以用合作博弈的方法来进行分析。也就是说，如果经济主体具备不受限制的缔约能力，那么，最终的结果必然是稳定的，因为任何不稳定的结果都会被某个联盟所推翻。夏普利及其合作者正是基于这种情形提出了各种匹配模型或算法，从而奠定了稳定配置理论的基础。

（二）稳定配置理论：Gale－Sharpley算法和顶端交易循环算法

1962年，盖尔和夏普利（1962）合作发表了题名为《大学录取和婚姻稳定性》的论文，阐述了双边市场的匹配问题。这里所谓的“双边市场”，就是指两个不相交的经济主体集合必须相互匹配才能完成交易活动的市场。通常，价格机制难以在双边市场上发挥有效的作用。以男女婚配为例，男人和女人必须相互匹配才能成婚，因而构成一种双边市场。而且，男女双方之间并不存在单方面的收益转移问题，这就是造成所谓的“价格机制难以发挥有效作用”的原因。

在这种情况下，男人和女人应该如何匹配才能达到最优状态呢？最理想的匹配方案是每个人正好跟自己的第一选择匹配。但是，这种匹配方案在大多数情况下会因需求的双重巧合问题而无法实现。那么，当最理想的方案无法实现时，如何匹配才能令人满意呢？盖尔和夏普利从合作博弈的角度认为稳定性是匹配的关键：如果没有任何一对男女能够通过另结联盟来提高自己的满意度，那么可以认为匹配是稳定的。这样的稳定配置满足两个条件：一是符合个人理性；二是实现两两稳定匹配。当匹配稳定时，就没有男人会喜欢除自己配偶以外的其他女人；同样，也没有女人会喜欢除自己配偶以外的其他男人，因此不存在任何一对男女背叛婚姻的情况。

接下来的问题就是：如何才能实现稳定的婚配？盖尔和夏普利提出了求解稳定配置的所谓的Gale－Sharpley算法，这种算法也被称为延迟接受算法（deferred－acceptance algorithm）。例1解释了用这种算法推演的具体匹配过程③，假设由男人先发出婚约。

［例1］双边市场：Gale－Sharpley算法。假设有4男（m1，m2，m3，m4）4女（w1，w2，w3，w4）要配对结婚，且结婚比单身好。男人和女人对对方有如下偏好：

第一轮配对：每个男人先挑选自己最喜欢的女人。如果一个女人收到一个以上男人发出的婚约，那么就接受其中她最喜欢的男人的婚约，并且拒绝其他男人的婚约；如果一个女人只收到一个男人的婚约，那么就接受他的婚约。这样，男人就分成婚约被接受和被拒绝两类。在所有的男人都找到配偶以后，计算就终止，即配对结束，否则就进入下一轮配对。经过第一轮配对，m1被拒绝，并有（m2，w4）、（m3，w1）、（m4，w2）三对男女配对成功④。

第二轮配对：所有被拒绝的男人向自己的次优选择对象发出婚约，每个女人都可以接受新的婚约，并接受自己最喜欢的男人发出的婚约，而拒绝其他男人的婚约。这样，原先婚约已经被接受的男人现在也可能遭到拒绝。当所有的男人都找到配偶以后，计算就终止，即配对结束，否则就进入再下一轮配对。计算或配对过程一直持续到所有男人都找到配偶为止。在这一轮配对中，m1向w3发出婚约，w3接受婚约，两人配对（m1，w3）成功。

这样，经过两轮配对，所有的男人都找到了配偶。配对过程结束，最终的配对结果是（m1，w3）、（m2，w4）、（m3，w1）、（m4，w2）。

那么，采用Gale－Sharpley算法完成的配对或配置具有哪些性质呢？盖尔和夏普利1962年证明：采用Gale－Sharpley算法完成的配置是稳定配置，且在参与人为数有限的配对情形中，经过有限轮次的配对之后总能找到稳定的配置，即所谓的“稳定配置存在性”。他俩对由男人发出婚约的Gale－Sharpley算法和由女人发出婚约的Gale－Sharpley算法进行了比较，并且证明了前者更有利于男人，而后者更有利于女人，即所谓的“匹配最优性”。他俩还证明了只有当男人的最优配对和女人的最优配对相一致时，配置才是唯一的，即所谓的“配置唯一性”。他们的结论可以概括为如下定理：

对于任何具有严格偏好的婚姻市场，

（i）存在性：至少存在一个稳定配置能使核集合非空，稳定的配置可以采用由男人发出婚约的Gale－Sharpley算法或者由女人发出婚约的Gale－Sharpley算法来得到。

（ii）最优性：用由男人发出婚约的 Gale－Sharpley算法得到的稳定匹配，对于男人而言是最优匹配，每个男人在核中找得对应最优的女性配偶，而女人却在核中找得对应最差的男性配偶；同理，用由女人发出婚约的Gale－Sharpley算法得到的稳定匹配，对于女人而言是最优匹配，每个女人在核中找得对应最优的男性配偶，而男人却在核中找得对应最差的女性配偶。

（iii）唯一性：当且仅当男人的最优匹配和女人的最优匹配一致时，核就包含一个唯一的配置。

Gale－Sharpley算法及其变体被广泛应用于双边市场匹配问题，如学生与学校、医生与医院以及雇员与雇主等等。然而，并不是所有的市场都是双边市场，现实中有些市场是单边的。所谓的单边市场，就是指像住房分配或者器官移植这样的市场。以器官移植为例，在器官移植手术中，移植器官受体要与移植器官供体进行配对，配对的一方，如移植器官受体，在配对过程中完全处于被动状态，这种情况不同于上述男人和女人双边配对中双方都积极寻找对方的情况。

那么，在单边市场的情况下，如何以有效的方式来完成配对呢？夏普利和斯卡夫在《论核与不可分割性》（Sharpley和Scarf，1974）一文中提出了解决单边市场匹配问题的顶端交易循环算法。这种算法仍然基于合作博弈的稳定性概念，采用定向表（directed graph），通过在初始配置的基础上进行互换（swap）来实现。例2解释了顶端交易循环算法的具体匹配过程。

［例2］单边市场：顶端交易循环算法。假设有四个参与人要与四种商品（A，B，C，D）进行配对，给定初始配置为四个参与人1、2、3、4分别拥有商品D、C、B、A，参与人对商品的偏好表示如下：

1：A＞B＞C＞D

2：B＞A＞D＞C

3：A＞B＞D＞C

4：D＞C＞A＞B

第一轮配对：制作定向表如下。根据定向表，参与人1和参与人4形成一个循环——参与人1偏好参与人4所拥有的商品，同时参与人4偏好参与人1所拥有的商品，他俩进行商品互换，并退出市场。剩下的参与人与商品进入下一轮配对。

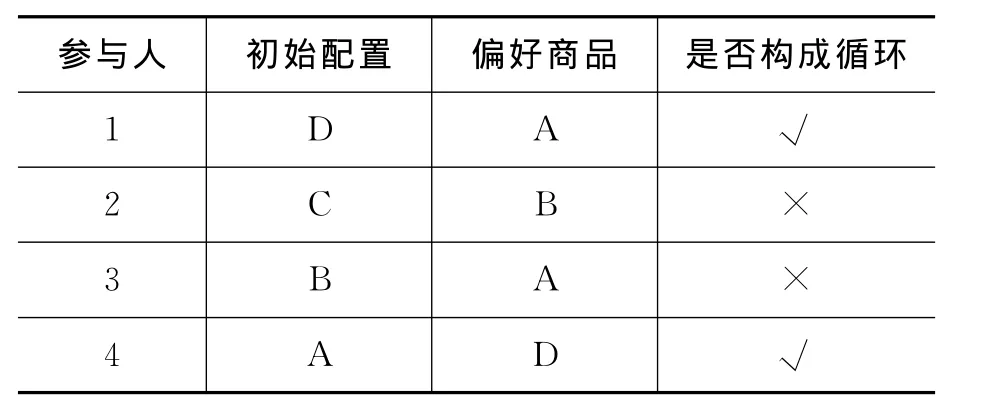
第二轮配对：制作定向表如下。如表所示，参与人2和参与人3都偏好商品B，因此，这轮配对不存在循环，而初始配置中参与人3拥有商品B，在此轮配对中参与人3保留其拥有的商品B，而参与人2只能保留自己拥有的商品C。配对到此结束，最终的配对结果是参与人1、2、3、4分别拥有商品 A、C、B、D。

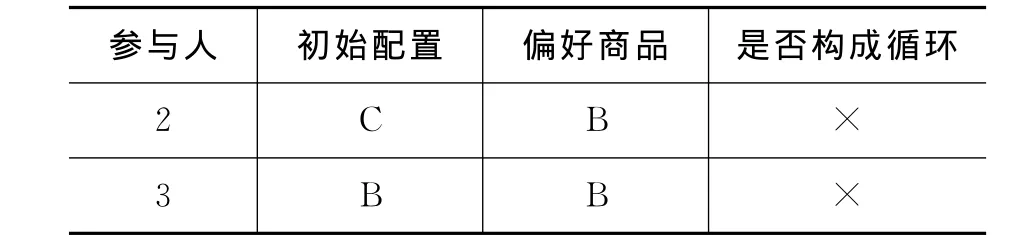
采用顶端交易循环算法的结果可能因初始配置的不同而不同。夏普利和斯卡夫证明顶端交易循环算法总能获得稳定的配置，即所谓的“稳定配置解的存在性”（Sharpley和Scarf，1974）。顶端交易循环算法及其变体可用来解决器官移植中的受体和供体配对问题。顶端交易循环算法和前述Gale－Shapley算法的最大意义在于：它们模拟了竞争性市场交易机制，参与人不必告诉自己的偏好，只按照算法规定的游戏规则做出选择，最终总会得到稳定的配置。夏普利的稳定配置理论有助于我们揭示匹配市场的实际运行机制，按照瑞典皇家科学院的说法，夏普利奠定了稳定配置理论的基石。

（三）市场设计：实证分析、实验研究及其应用

20世纪60年代，夏普利的稳定配置理论及其算法研究主要停留在理论层面。到80年代初，它们的实践价值还没有被充分挖掘出来。直到1984年，罗思发现了NRMP，才找到了稳定配置理论及其算法的现实实用性。罗思也因此打开了市场设计的大门，并开创了经济工程学（economic engineering）研究这个新领域。

罗思在《医学院实习生与住院医生劳动力市场演变：博弈论案例研究》（Roth，1984）一文中研究了美国新医生市场演变问题。在美国，医学院毕业生通常被作为实习住院医生受雇于医院，这些毕业生是医生市场的一个重要组成部分。20世纪40年代，美国医院对实习住院医生的强大需求导致医院为雇用实习住院医生而展开激烈的竞争。于是，医院越来越早地为医学院学生提供实习医生职位，甚至给那些还有几年才毕业的学生提供实习职位。这种过早的签约行为产生了很多负面影响，其中最大的问题是大部分学生还没获得任职资格就进医院当住院医生。除此之外，这个市场还饱受拥挤之苦：等医学院学生拒绝聘约，医院再向其他学生发聘约就已经太迟了。医院为争取主动而采用多发聘约的办法，并通常会设定严格的报到期限，结果导致学生必须在还不知道是否有其他就业机会的情况下做出自己的选择。通过后续研究，罗思进一步发现，这种过早签约和拥挤现象不止存在于美国新医生市场，而且还困扰着很多其他市场（Roth和Xing，1994），其结果是导致不稳定的市场配置。

为了解决上述市场失灵问题，美国在20世纪50年代初引入了NRMP。该计划由Stalknaker和Mullen于1952年设计制定，比盖尔和夏普利提出的算法要早10年之久。罗思发现NRMP所使用的算法等价于Gale－Sharpley算法，并且令人信服地论证道：NRMP能够成功的关键在于NRMP算法所实行的配置具有稳定性，否则实习医生和医院都有动机在NRMP之外进行重新匹配。NRMP的这个特性吸引了很多实习医生和医院加入该计划，从而增加了市场厚度（thickness），使市场有足够多的交易机会，进而又进一步吸引其他人加入该计划，这样就形成了良性循环。类似的情况也存在于英国区域医疗市场，一些地区成功地采用了等价于Gale－Sharpley算法的算法，并数十年不变；而另一些地区采用的算法由于配置结果不稳定而被淘汰。

实验经济学的兴起和发展使得在实验室中进行匹配算法研究更有条件，从而也有助于我们更好地理解各种匹配算法的优缺点。罗思对匹配算法的实验经济学研究证实了稳定算法能够避免市场失灵。他在《作为工程师的经济学家：把博弈论、实验和计算作为设计经济学的研究工具》（Roth，2002）一文中倡议采用工程学方法来进行市场设计，认为充分利用实验经济学和计算经济学研究方法将有助于弥补博弈论工具的不足。罗斯的倡议反过来又推动了罗思对实验经济学的研究。如前所述，罗思也是实验经济学领域一个重要的代表人物。

罗思对稳定配置理论的贡献不仅表现在他从理论上对稳定配置理论进行的深入研究，更重要的是体现在他亲自推动了市场设计实践活动的发展。在他的推动下，新的市场设计成果不断涌现，为了修复市场失灵，一些原来存在缺陷的市场设计方案又根据其具体的应用环境和伦理道德约束等进行了重新设计。以下三个市场设计案例能够反映罗思对市场设计或重新设计做出的贡献。

第一个案例就是对NRMP的重新设计。医生劳动力市场的结构性变化对NRMP原来采用的算法提出了挑战。医生有未婚和已婚之分，原先的NRMP算法只是针对未婚医生设计的。罗思已经证明该算法能实现未婚医生的稳定匹配，同时能够阻止他们采取策略性行为，因此成功地运行了很多年。但到了20世纪60年代以后，医生市场发生了变化，越来越多的已婚医生夫妇从医学院毕业，他们通常会绕过NRMP直接跟医院联系工作。1997年，罗思对NRMP进行了重新设计，以确保已婚医生夫妇也能实现稳定的匹配。每年有2万多名医生通过罗思重新设计的算法实现了稳定匹配（Roth，1999）。

第二个案例就是罗思帮助设计的纽约公立学校匹配系统和波士顿公立学校匹配系统。原先纽约公立学校学生和学校双向选择的做法是，先由学生按自己的偏好填报五所学校，然后由学区分别寄送给各相关学校。这样，每所学校都能知道自己是不是学生的首选，从而会导致学生有动机隐匿自己的真实偏好。罗思及其合作者于2003年设计了一种激励相容机制，后来纽约公立学校的校委会就用它来录取新生。类似的问题也存在于波士顿公立学校，它们过分看重学生的第一志愿，以至于学生一旦没有被第一志愿的学校录取，就很可能遭到其他学校拒绝，而遭到拒绝的学生最终只能通过行政手段被分配给有空缺的学校。显然，这样无法达到资源的最优配置。罗思及其合作者为纽约公立学校重新设计的匹配算法结果于2004年也被波士顿当局所采纳。

第三个案例就是新英格兰肾脏移植计划。罗思是新英格兰肾脏移植计划创立者之一。这项计划是对顶端交易循环算法的改进和应用。前文所述的顶端交易循环算法应用到像肾脏移植这样的单边匹配市场中会遇到一些困难，因为顶端交易循环算法要求所有的参与人同时进行匹配，而肾脏移植会遇到受体与供体不相容的问题，一些病人必须等待合适的肾源，而且等待过程可能相当长。罗思等人对顶端交易循环算法进行了改进，设计了一种复杂的多边互换交易算法。“新英格兰肾脏移植计划”算法现在也被美国很多州采纳。

从上述分析可以看出，具体应用会碰到新的问题，新的问题又会刺激理论研究的发展，反过来又促进新的应用。罗思对市场设计的研究生动地展示了理论和实践的相互促进作用：理论研究有助于加深对现实经济的理解，而现实市场设计的需要又反过来推动理论研究的发展。

罗思是市场设计研究领域的先驱，他在《我们从市场设计中学到了什么？》（Roth，2009）一文中总结了他在设计市场机制以修复市场失灵的过程中积累的主要经验和教训。罗思归纳了为市场良好运行所必需的条件：（1）市场必须有足够的厚度，也就是说，必须能够吸引足够多的潜在交易者入市交易；（2）克服市场厚度不够所导致的市场拥挤（congestion），允许市场参与人在充分考虑各种可能的交易机会后选择自己满意的交易，这个条件可以通过提供足够的时间或者使交易尽快完成来满足；（3）保证参与市场交易比场外交易更加可靠、安全，并且尽可能简单，不会因受策略性行为的干扰而导致福利减少。此外，他附带谈到了两条关于具体的市场设计实践和方法的重要教训：（1）就市场设计实践而言，可能会出现许多令人讨厌的市场交易，这是进行市场设计时必须考虑的一个重要约束因素；（2）从方法论的角度看，要充分发挥实验经济学在市场设计中的作用，包括利用实验经济学方法诊断和理解市场的成功之处和失败之处，检验新的市场设计方案的可能表现，采用实验经济学方法向政策制定者展示市场设计方案，并与他们进行沟通，以便他们更好地理解设计方案。

（四）其他贡献：夏普利值及其变体

夏普利为合作博弈论的扩展和应用做出了卓越的贡献，在博弈论中有很多以“夏普利”命名的概念，其中最重要的当属夏普利值⑤。夏普利最早在其博士论文中提出了夏普利值的概念，此后进一步发展了这个概念，使其成为解决合作博弈公平分配问题最常用的一个解概念。夏普利值的基本思想是公平分配要遵循报酬与贡献相等的原则。例3中的例子体现了这一思想的精髓。

［例3］公平分配问题。举一个例子：甲、乙两人各有3只和5只饼。他俩与第三个人丙一起把8只饼吃了。随后，丙共付给甲、乙两人8枚金币作为报酬。甲、乙为如何分这8枚金币发生了争执。甲认为，饼是一起吃的，因此，这8枚金币应该由他俩平分，即各得4枚；而乙则认为，他出了5只饼，因此该得5枚金币；甲只出了3只饼，该得3枚。那么，究竟如何才能公平⑥分配这8枚金币呢？按照报酬与贡献相等的原则，8只饼3人平分，每人吃了8／3只饼，甲出了3只饼，因此，在丙支付的8枚金币中，甲贡献了3－8／3＝1／3只饼；同理，可以算出乙的贡献是7／3只饼。于是，公平的分配应该是甲得1枚金币，乙得7枚金币。这个例子反映了夏普利值的精髓。

1953年，夏普利在其论文《N参与人博弈值》（Sharpley，1953）中，提出了一个能用于识别合作博弈每个参与人唯一收益的公理集，即所谓的“夏普利值”。夏普利在这篇论文中对夏普利值的思想进行了公理化，从而大大扩大了夏普利值在解决利益分配和成本分摊等经济问题中的应用。例4中的联合成本分摊正是夏普利值在成本分摊问题上的一种直接应用，该例遵循的是付出与所得相等的原则。

［例4］联合成本分摊。假设有甲、乙、丙、丁四个家庭居住在同一条通往高速公路但还没铺设完的公路旁。甲、乙、丙、丁分别距离高速公路200米、900米、1000米和2900米。假设铺好公路的成本为每100米1000元，如果他们愿意分摊成本，那么，应该如何公平分摊29000元的总成本呢？

一个解决方案是按比例分摊成本，即甲、乙、丙、丁按照0.2∶0.9∶1∶2.9的比例来分摊29000元的总成本。这样，甲、乙、丙、丁分别承担1160元、5220元、5800元和16820元。但是，这个成本分摊方案是不稳定的。因为，如果乙和丙联手共同完成两家通往高速公路的公路铺设工程，那么共需承担10000元的成本，小于两人按比例须承担的成本11020元（即5220元＋5800元）。夏普利值提供了一种稳定的合作解：按照付出与所得相等的原则，最初的200米由于4家都要用，因此由4家平摊成本，甲应支付500元；接下来的700米由乙、丙、丁共用，因而应由这三家共同平摊成本，乙应该支付2833元（＝500元＋7000／3元）；以此类推，丙和丁各承担3333元和22333元。

夏普利值的提出引起了广泛的争议，许多经济学家对原先的夏普利公式进行了修改，并在此基础上得出了多个能应用于不同经济情境的夏普利值变体，其中最重要的一个变体是由夏普利本人及其合作者苏彼克在他俩1954年发表的分析联合国安理会不同成员国影响力的论文《评估委员会制度中权力分配的一种方法》中提出的，这个变体就是所谓的“Shapley－Shubik权力指数”（Shapley－Shubik power index）。Shapley－Shubik权力指数及其更一般的版本被广泛应用于量化不同投票规则下个人投票者的影响以及团体决策等问题。例5旨在解释Shapley－Shubik权力指数的应用问题。

［例5］Sharpley－Shubik权力指数。假设有A、B、C三个人共同投票决定总额为100万美元的资金分配方案，投票采用多数通过原则，即资金分配方案只有获得严格超过50%的票数才能通过。假设A、B、C分别拥有50%、30%、20%的投票权，那么，应该如何合理制定资金分配方案呢？

一种解决方案是按投票权比例分配资金，A、B、C分别分得50万、30万、20万美元。但是，按这个方案分配的结果也是不稳定的。例如，B可以向A提议结盟一起排挤C，然后瓜分C应得的20万美元，如此等等。Shapley－Shubik权力指数提供了另一种解决方案：先对A、B、C三人进行排列组合，得到可能结成联盟的全部有序组合，A、B、C三人能够形成的所有有序组合（即联盟）为ABC、ACB、BAC、BCA、CAB、CBA；然后确定能使有序组合获胜的参与人，即关键参与人，如对于有序组合ABC，B是关键参与人，而其余有序组合的关键参与人分别是C、A、A、A、A；最后确定A、B、C三人分别在所有可能的有序组合中成为关键参与人的次数，得到所谓的权力指数。权力指数占全部可能有序组合的比例就是夏普利值。在本例中，A、B、C的权力指数分别为4、1和1，他们的夏普利值分别为4／6、1／6和1／6。因此，他们分别可分得100万美元的4／6、1／6和1／6。

四、夏普利和罗思贡献的理论意义和实践价值

正如本文开宗明义指出的那样，人类的社会经济活动总是在冲突与合作中发展，冲突中有合作，合作中有冲突，构成了多姿多彩的社会经济活动。从冲突与合作的视角看，社会经济制度的设计和构建要充分考虑冲突与合作的有机统一，要把冲突与合作的互动因素考虑进去，以使人们既能够自由选择各自的行为，又能够避免那些谁都不愿意选择的结果（Bowles，2006）。众多不同的经济学理论，如哈耶克的自发扩展秩序原理、布坎南的公共选择理论、科斯的新制度经济学、诺斯的国家理论、赫维茨的机制设计理论等等，从某种意义上说都是为了在冲突与合作无处不在的现实世界中寻找提高人类福祉的路径而做出的努力。就此而言，夏普利的稳定配置理论和罗思的市场设计方法也是这种努力的结果。它们所强调的在冲突中谋求合作以有效配置资源之道，无论是对现在还是未来化解冲突问题，都具有深远的理论和实践意义。

对我国而言，经过30多年的改革开放，市场机制的引入及其在资源配置中发挥的基础性作用大大提高了资源配置的效率。但也要看到，市场失效的问题也日益显现。因此，借鉴夏普利的稳定配置理论和罗思的市场设计方法来解决我国社会经济发展过程中遇到的一些现实问题，是十分必要的。比如，已有国内研究人员借鉴罗思的学生与学校匹配研究成果探讨了我国高考录取与博士生录取机制设计问题（魏立佳，2009），实际上学生与学校的双向选择问题不仅存在于大学，也普遍存在于初中和高中，构建稳定而又高效的匹配机制是我国教育体制改革所要解决的重要课题之一。再者，器官移植问题也是一个与稳定配置和市场设计直接相关的现实问题，2012年我国卫生部人体器官移植技术临床应用委员会讨论通过了《中国人体器官获取与分配管理办法（试行）》。该办法对器官获取组织进行了规范，规定今后器官移植试点医院如获得器官，必须由中国器官分配与共享系统来分配⑦。不过，这个共享系统的稳定性和效率仍然有待检验。此外，经济适用房、机动车牌照摇号分配等问题也可以用稳定配置理论和市场设计方法来解决。

与此同时，随着改革的进一步深入，利益主体日益多元化和复杂化，特别是在当前社会经济转型的关键时期，各种社会经济矛盾、利益冲突纷繁复杂，相互交织在一起。对于如何通过合作来化解冲突从而优化资源配置，夏普利和罗思的理论及其应用无疑有直接的启发意义和借鉴价值。尤其是夏普利值提供的公平分配方案可以为我国的收入分配改革方案提供某些指导；还有如跨省、跨市的公共建设以及农村公共道路建设中的成本分摊问题，也可以借用夏普利值来解决。

总之，深入理解夏普利在合作博弈理论扩展和应用方面做出的贡献以及罗思对市场设计的贡献，以合作博弈论作为补充，综合运用非合作博弈论和合作博弈论的研究方法，深入研究现实生活中的各种社会经济问题，有助于全面把握社会经济生活中的冲突与合作问题，有助于通过系统整合相关的经济理论来全面理解现代经济社会的运行规律。

注释：

①读者如想更全面地了解合作博弈理论，可以参阅莫林著的《合作的微观经济学：一种博弈论的阐释》，格致出版社、上海三联出版社、上海人民出版社，2011。

②例如，由3个参与人构成的集合N＝｛1，2，3｝可能结成如下7个联盟：｛1｝、｛2｝、｛3｝、｛1，2｝、｛1，3｝、｛2，3｝、｛1，2，3｝，其中｛1｝、｛2｝、｛3｝是单人联盟，｛1，2，3｝是统一战线联盟。

③文中例1和例2改编自瑞典皇家科学院的新闻公告；例4取自莫林《合作的微观经济学：一个博弈论的阐释》第2章；例5改编自夏普利和舒彼克的论文（Shapley和Shubik，1954）。

④这三个配对只是接受订婚但并没有马上成婚，这就是所谓的“延迟接受”（deferred acceptance）。

⑤有关夏普利值的理论及其扩展，可参阅罗思1988年编著的《夏普利值：向劳埃德·S·夏普利致敬》一书。

⑥这里的公平是基于所得与贡献相等原则的公平，不等同于绝对平均主义公平。

⑦读者可以参考相关的网络报道，http：／／szbk.wnrb.net／html／2012－10／11／content＿1542835.htm。

［1］Ashlagi I and Roth A E.New challenges in multi－hospital kidney exchange［J］.American Economic Review，2012，102（2）：354－359.

［2］Edelman B，et al.Internet advertising and the generalized second－price auction：Selling billions of dollars worth of keywords［J］.American Economic Review，2007，97（2）：242－259.

［3］Gale D and Shapley L S.College admissions and the stability of marriage［J］.American Mathematical Monthly，1962，69（1）：9－15.

［4］McKinney C N，et al.The collapse of a medical labor clearinghouse（and why such failures are rare）［J］.American Economic Review，2005，95（3）：878－889.

［5］Roth A E.The economics of matching：Stability and incentives［J］.Mathematics of Operations Research，1982，7（4）：617－628.

［6］Roth，A E.The evolution of the labor market for medical interns and residents：A case study in game theory［J］.Journal of Political Economy，1984a，92（6）：991－1016.

［7］Roth A E.Misrepresentation and stability in the marriage problem［J］.Journal of Economic Theory，1984b，34（2）：383－387.

［8］Roth A E.A natural experiment in the organization of entry level labor markets：Regional markets for new physicians and surgeons in the UK［J］.American Economic Review，1991，81（3）：415－40.

［9］Roth A E.Repugnance as a constraint on markets［J］.Journal of Economic Perspectives，2007，21（1）：37－58.

［10］Roth A E.What have we learned from market design？［J］.Economic Journal，2008，118（2）：285－310.

［11］Roth A E and Xing X.Jumping the gun：Imperfections and institutions related to the timing of market transactions［J］.American Economic Review，1994，84（4）：992－1044.

［12］Roth A E and Rothblum U.Truncation strategies in matching markets：In search of advice for participants［J］.Econometrica，1999，67（1）：21－43.

［13］Roth A E and Peranson E.The redesign of the matching market for American physicians：Some engineering aspects of economic design［J］.American Economic Review，1999，89（4）：748－779.

［14］Roth A E，et al.Kidney exchange［J］.Quarterly Journal of Economics，2004，119（3）：457－488.

［15］Roth A E and Sotomayor M.Two－sided matching：A study in game－theoretic modeling and analysis［M］.Cambridge：Cambridge University Press，1990.

［16］Serrano R.Cooperative games：Core and Shapley value［A］.Meyers R（Ed.）.Encyclopedia of complexity and systems science［C］.New York：Springer，2009.

［17］Shapley L S.A value for n－person games［A］.Kuhn H W and Tucker A W （Eds.）.Contributions to the theory of games（Vol.2）［C］.Princeton，NJ：Princeton University Press，1953.

［18］Shapley L S.Markets as cooperative games［R］.Rand Corporation Memorandum P－629，1955.

［19］Shapley L S.On balanced sets and cores［J］.Navel Research Logistics Quarterly，1967，9（1）：45－48.

［20］Shapley L S.Cores of convex games［J］.International Journal of Game Theory，1971，1（1）：11－26.

［21］Shapley L S and Shubik M.A method of evaluating the distribution of power in a committee system［J］.American Political Science Review，1954，48（1）：787－792

［22］Shapley L S and Shubik M.The assignment game I：The core［J］.International Journal of Game Theory，1971，1（1）：111－130.

［23］Shapley L S and Scarf H.On cores and indivisibility［J］.Journal of Mathematical Economics，1974，1（1）：23－37.

［24］The Royal Swedish Academy of Sciences.Stable allocations and the practice of market design［EB／OL］.Royal Swedish Academy of Sciences，2012.

［25］The Royal Swedish Academy of Sciences.Stable matching：Theory，evidence，and practical design［EB／OL］.Royal Swedish Academy of Sciences，2012.

［26］董保民等.合作博弈论［M］.北京：中国市场出版社，2008.

［27］郭其友，李宝良.冲突与合作：博弈理论的扩展与应用［J］.外国经济与管理，2005，（11）：1－11.

［28］郭其友，李宝良.机制设计理论：资源最优配置机制性质的解释与应用［J］.外国经济与管理，2007，（11）：1－8.

［29］何维·莫林著.合作的微观经济学——一种博弈论的阐释［M］.（童乙伦，梁碧译）.上海：格致出版社，上海三联出版社，上海人民出版社，2011.

［30］萨谬·鲍尔斯著.微观经济学：行为、制度与演化［M］.（江艇等译）.北京：中国人民大学出版社，2006.

［31］魏立佳.中国高考录取与博士生录取的机制设计［J］.经济学（季刊），2009，（1）：349－362.