多指标面板数据聚类方法及其应用

任娟

（南京航空航天大学 经济与管理学院，南京 210016）

0 引言

面板数据结合了截面数据和时间序列数据的特征，具有优良的特性，在研究中日益受到重视。然而，国内外很少学者考虑面板数据的多元统计分析。Bonzo D.C.和Hermosilla A.Y.[1]开创性地将多元统计方法引入面板数据的分析中，并用概率连接函数和遗传算法改进了聚类分析。Ren J.[2]基于Fisher有序聚类理论，通过Frobenius范数重建了Ward函数，提出了一种多指标面板数据有序聚类方法。该方法没有考虑指标的动态性，如指标的增长速度等。朱建平和陈民垦[3]对单指标面板数据的聚类分析进行了研究，其聚类算法和聚类过程类似于截面数据的聚类分析。李因果和何晓群[4]综合考虑了面板数据的“绝对指标”和“增量指标”，在重构面板数据相似性测度的基础上，提出了面板数据聚类方法。这种方法的不足之处是它对指标的增长速度的局部变化不能进行区分。另外，以上方法都是假设时间序列是同步的，但是，在现实世界中，这一条件并不总能满足，许多情况下它们是非同步的。因此，本文认为应综合考虑面板数据水平指标、增量指标、增量变化率指标及其非同步时间序列问题，为解决多指标面板数据聚类问题，拟提出一种面板数据聚类方法。

1 面板数据的数据格式

1.1 单指标面板数据

单指标面板数据的数据格式可以用一个二维表来表示。单指标面板数据聚类分析有两种处理方法：一种是转换方法，将单指标面板数据的时间维度转换为截面数据的指标维度表示，两种数据的统计描述特征相似，在聚类分析中，二者关于样品距离的算法、聚类过程都是相同的，因此，单指标面板数据的聚类分析可以借鉴截面数据的聚类分析，可以直接运行相关软件进行计算。另一种是一维有序样品聚类方法，将单指标面板数据的空间维度转换为有序样品的指标维度表示，但需要进行降维处理得到一维指标。目前有不少专业软件可以完成一维样品有序聚类计算，比如DPS等。

1.2 多指标面板数据

在实际中，由于现象的复杂性，研究对象往往表现为多指标面板数据X，它表示一个样本。多指标面板数据的结构要复杂一些，严格上应该用三维表来表示，也可以将其表示为矩阵形式。设一个样本X包括的q个样品，每个样品的特征用p个指标描述，时间序列长度为T，实际上多指标面板数据含有空间（样品）、指标和时间三个维度。

样本X在空间维度上可表示为一组“空间样品”，也就是将三维表在空间上展开为二维表，即：样本X的一个“空间样品”Xi的矩阵表示为：

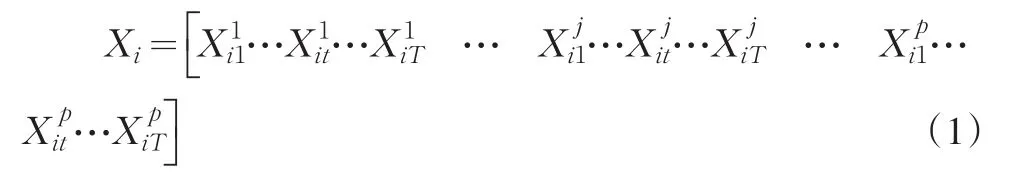
2 多指标面板数据的时间序列特征

依据已有文献，按照聚类分析处理面板数据的方法有：（1）每年分别进行聚类，显然会造成各年度分类结果的不一致。（2）采取退化方法，对指标取其年度平均值进行聚类，消去时间维度，显然损失了指标的时间维度信息。（3）采取简化方法，不考虑指标的时序性，认为各时点上的指标对欧氏距离的贡献程度一样，显然，忽视了指标的时间维度信息。（4）仅采用指标的水平值或者增量进行聚类，这种聚类结果不是忽视了指标的动态性，就是抹杀了指标的水平状态。（5）采取综合方法，采用指标的水平值和增量进行聚类，虽然提取了增量时间序列信息，但没有进一步提取增量变化率时间序列信息。

显然，上述五种聚类思路都存在一定的缺陷，对多指标面板数据的聚类：一方面要考虑样本指标间的距离，另一方面必须考虑其时间序列的动态发展特征。因此，构造相似性指标时，必须考虑面板数据的水平指标、增量指标和增量变化率指标的时间序列。其中，水平指标的时间序列是第i个样品的单个水平指标构成的时间序列增量指标的时间序列是将时间序列进行一阶差分得到的序列，其中，增量变化率指标的时间序列是将时间序列进行二阶差分得到的序列，其中：

3 聚类方法及聚类步骤

聚类分析是对q个样品进行分类或对p个指标进行分类，其中前者称为Q型聚类，后者称为R型聚类。聚类分析有两个关键问题：一是衡量样品（或变量）间邻近或相似程度的度量，另一个是聚类方法。

聚类分析常用的距离有绝对距离、欧氏距离、明考斯基距离、切比雪夫距离妙、马氏距离等。常用的相似系数有夹角余弦、相关系数等。虽然多指标面板数据与截面数据的欧式距离有差异，但只是形式上的差异，本质上是一致的。这里，考虑采用样本各指标的水平值、增量、增量变化率时间系列提取面板数据时间维度信息，选择欧式距离来描述样品之间的邻近程度，即第u样品与第v样品之间的欧式距离d(u,v)为：

其中：

共3T-3个变量用来描述第i个样品的第j个指标的水平值、增量、增量变化率时间序列，记为并用表示第i个样品Xi。

样品欧式距离d(u,v)可以认为是样品间水平值、增量、增量变化率时间序列的三种距离的加权求和。权重一般根据实际问题进行设定，本文认为它们是等权重的。

考虑不同样品的不同时期的相似性测度问题，则第u个样品滞后h期与第v个样品的滞后k期的欧式距离d(u-h,v-k)为：

其中：

用来描述第i个样品的第j个指标滞后k期的水平值、增量、增量变化率时间系列，记为表示第i个样品滞后k期为计算欧式距离时，对应的时间序列长度必须是相同的。

用于计算欧式距离的指标需满足以下条件：指标之间不相关；消除各指标量纲的影响。相应的解决方法：原始数据通过因子分析得到的公共因子是不相关的；数据标准化处理即可消除量纲的影响。

实际应用中可根据指标重要性进行加权修正，权重系数可以根据研究问题的实际情况主观给定或客观测定，如实践中常用的专家调查法，AHP，模糊判别，方差贡献，熵权系数等方法确定权重系数。

聚类方法有系统聚类法、分解聚类法、有序样品聚类法、动态聚类法、模糊聚类法等多种，其中，系统聚类法是目前国内外使用得最多的一种聚类方法。系统聚类法按类间距离的不同定义又可分为最短距离法、最长距离法、平均距离法、重心距离法和离差平方和法等。这里仅讨论离差平方和法。

在类Gu中的样品的离差平方和为：

其中，i∈Gu表示样品Xi是类Gu中的一个样品表示类Gu的第j指标在t时间的均值是类Gu中样品的个数。

Wald认为两类合并时所增加的离差平方和可以定义为两类的平方距离。类Gu和类Gv间的离差平方和距离D2(u,v)定义为：

其中，Su、Sv和Sl分别是在类Gu和Gv以及它们并成的新类Gl中样品的离差平方和，s和t分别是类Gu和Gv中样品的个数，分别是类Gu和Gv的重心，分别表示Xi是类Gu和Gv中的一个样品。

离差平方和法的递推公式：在类Gm和类Gq合并成新类Gr后，新类Gr与另一类Gk的距离D(k,r)可表示为：

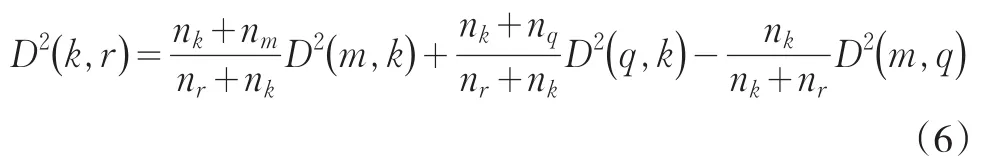
其中nk、nm、nr和nq分别表示类Gk、Gm、Gr和Gq中样品的个数。

系统聚类的计算步骤包括：定义样品间距离，计算样品两两间距离构成的距离矩阵；合并距离最近的两类为一新类，计算新类与当前各类的距离；如此循环，直至并为一类为止；画聚类图。

4 实证分析

4.1 聚类结果及分析

本文采用平均价格指标及其增量、增量变化率衡量公司的差异化战略，采用销售量指标及其增量、增量变化率衡量公司的低成本战略。基于2009年3月～2010年3月国内空调市场上24个品牌（总的市场占有率为98%）的营销统计数据，对24个品牌进行了聚类分析。数据来源于中怡康公司中国城市家电市场零售监测报告。战略变量的描述涉及平均价格和销售量两个关键指标。数据的处理采用SPSS16.0和Matlab7.4软件。聚类结果如图1所示。第一类为海信、松下、三星、LG、三菱电机、日立、三菱重工、夏普和大金共9个品牌，这类企业产品平均价格高，价格波动小，溢价能力强，市场占有率比较稳定，采用差异化战略参与市场竞争。其中，日立、三菱电机、三菱重工、夏普、松下均为日本品牌,三星、大金、LG则为韩国品牌,仅有海信为本土品牌。显示日韩企业在中国市场的竞争策略甚为接近，在广大的中国市场上不追求市场占有率,采取稳扎稳打的策略,这是日韩企业近年来采用轻资产战略(降低重资产、增加无形资产)的结果。海信作为变频空调龙头企业，注重技术创新和产品质量，竞争战略与日韩企业相似。第二类为新科、扬子、奥克斯、志高、惠而浦、长虹、科龙、TCL、格兰仕、新飞和春兰共10个品牌。除了惠而浦为美国品牌，其余全为本土品牌。这类企业产品平均价格较低，价格波动大，市场占有率不稳定，倾向于价格战来争夺市场份额，溢价能力弱，创新能力不足，推出新产品较少，采用低成本战略参与市场竞争。第三类为伊莱克斯。伊莱克斯为瑞典品牌，其产品平均价格较高，价格波动大，溢价能力一般，既追求市场份额，又塑造高档形象；体现为在低端路线和高端路线的选择上摇摆不定，这是因为伊莱克斯正处在由低端产品向高端产品战略的转型时期，陷入了“夹在中间”的困境。第四类为格力、美的和海尔。其产品平均价格较高，价格波动较大，市场占有率高，产品溢价能力强，创新能力强，新产品推出较多。采用低成本和差异化战略参与市场竞争。

图1 面板数据聚类分析谱系图

4.2 面板数据聚类方法比较分析

为说明本文提出的聚类方法的优越性，下面采用上例的数据来进行验证，并给出本文方法和文[4]的多指标面板数据聚类方法分类效果的比较。

文[4]采用水平指标和增量指标进行面板数据聚类，一定程度上刻画了水平指标的发展变化情况，但是没有进一步对增量变化程度的刻画，所得分类结果不够细致。本文方法采用水平指标、增量指标和增量变化率指标综合测度面板数据的样品相似性，提取信息比较充分，所得分类结果（图1）比较细致。另外，实际应用中，根据研究问题的实际情况也可采用三种量的组合进行聚类。

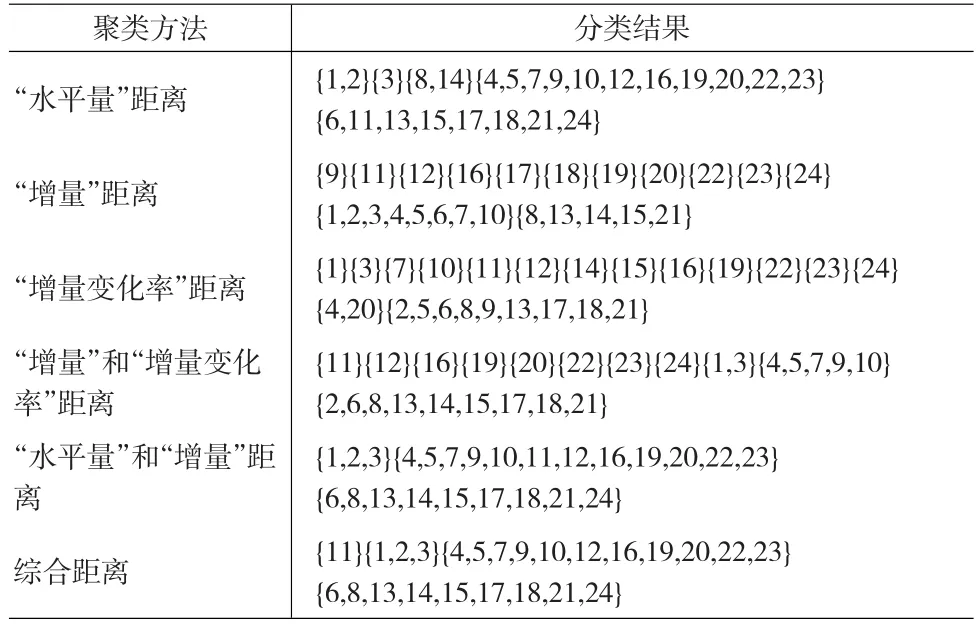
表1 24个空调品牌的面板数据聚类结果

5 结论

本文聚类方法特别适用于针对具有多指标的面板数据的样品分类问题，综合考虑面板数据的水平指标、增量指标和增量变化率指标的时间序列特征及其非同步时间序列问题，重新构造了离差平方和函数，提出了一种多指标面板数据聚类方法。通过实证分析，表明新方法能够解决多指标面板数据聚类的问题，分类效果较好。但是分类规模较大时，分类将呈现组合爆炸的趋势，计算量随着急剧增加，寻找最优解变得困难，对于采用遗传算法等人工智能方法搜寻次优解有待于将来进一步的研究。

[1]Bonzo D C，Hermosilla A Y．Clustering Panel Data via Perturbed Adaptive Simulated Annealing and Genetic Algorithms[J].Advances in Complex Systems，2002，（4）．

[2]朱建平，陈民垦.面板数据的聚类分析及其应用[J].统计研究，2007，（4）．

[3]Ren J，Shi Sh L.Multivariable Panel Data Ordinal Clustering and Its Application in Competitive Strategy Identification of Appliance-wir⁃ing Listed Companies[C].International Conference on Management Science＆ Engineering(16th)，Moscow，Russia，2009．

[4]李因果，何晓群.面板数据聚类方法及其应用[J].统计研究，2010，（9）．