基于Dirichlet过程无限混合模型的基因表达数据聚类算法

张 林，刘 辉

（中国矿业大学 信息与电气工程学院，江苏 徐州 221116）

0 引言

近年来基因芯片、基因表达数据的出现导致基因表达数据的爆炸性增长，有关DNA基因表达数据的生物信息学研究方法发展迅速。基于高通量的DNA基因表达数据实现相关预测已成为生物医学实验检测技术的重要补充。如何从具备高维度、小样本、高冗余特征的基因表达数据中利用计算机分析工具得到有用的信息，已成为基因表达数据分析的主要内容。聚类分析作为一种重要的数据分析方法，在基因表达数据的分析中已有广泛的应用，如通过对样本的聚类分析自动对不同的疾病亚型或实验条件实现区分，通过对基因聚类发现未知基因的功能，等等。

大多基于模型的聚类算法在假设给定聚类数的前提下，根据待聚类样本的属性，建立有限混合模型对基因表达数据展开研究，模型中聚类数的确定问题通常通过模型选择问题加以解决，因而聚类的准确性和泛化性受到模型选择准则的影响。作为无限混合模型核心的Dirichlet过程，则被广泛应用于解决传统的有限混合模型中子模型个数不确定的难题。

本文拟基于DNA基因表达数据建立Dirichlet过程无限混合模型展开聚类分析，其中的聚类数将由模型和数据自主计算得出[1～3]，无需独立确定，因而更为灵活。

1 基因表达数据的Dirichlet无限混合模型

1.1 DNA基因表达数据

DNA基因表达数据通过荷载成千上万个基因片段，实现高通量的生物学检测，使得从整个人类基因组研究基因的表达与调控成为可能。但DNA基因表达数据实验中如荧光标记效率、扫描参数设置、空间位置差异等各种变异都是基因表达水平原始数据中噪声产生的来源。因此，DNA基因表达数据需要经过标准化，以消除由于系统变异引起的误差。经过预处理的DNA基因表达数据通常服从正态分布p(μ,σ2)。

1.2 基因表达数据的Dirichlet过程混合模型

用X={x1,x2,…xN}表示DNA基因表达数据，N表示数据中包含的样本个数，xi={xi1,…xiG}T表示第i个样本，则xig表示第i个样本第g个基因的表达水平，各样本间相互独立。X可由K个正态模型混合而成（K未知）。为求解K，本文定义一隐变量s={s1,…,sN}(si∈{1,…,K})表示样本的聚类标签，si=k表示第i个样本经过聚类分析属于第k类。用p(⋅)表示模型中各成分模型，各自遵照不同的分布参数θk，θk={μk,σk2}，μk表示第k个成分模型的均值，σk2表示方差。πk表示第k个成分模型的混合系数，满足 πk≥0,k={1,…,K}并且假设 Θ={π1,…,πK;θ1,…,θK;K}，则 Θ 表示模型中所有待求参数，则基于DNA基因表达数据可建立如式（1）所示的正态混合模型。

因此，本文的目标即估计上述正态混合模型中的参数Θ。目前，求解此类问题的方法大概有两种，一是期望值最大化算法（EM：Expectation Maximization），二是Bayesian随机采样算法。EM算法主要用于在极大似然准则下估计模型参数，一直是有限混合模型参数估计问题的标准算法之一，但该算法容易陷入局部极值点。本文基于后种方法求解，采用Dirichlet过程作为先验分布，建立DNA基因表达数据的Dirichlet过程无限混合模型，利用基于Gibbs采样的MCMC方法估计出Θ的后验分布[4]。

Dirichlet过程基于Dirichlet分布生成，作为分布上的分布，是Dirichlet分布在连续空间上的扩展。通常，Dirichlet过程表示为

其中，G0是基分布；α(α＞0)是集中度参数，表示G逼近G0的程度；G表示基于Dirichlet过程在基分布和集中度参数基础上产生的某随机分布。α越大，G越接近G0。

因此，本文基于DNA基因表达数据建立Dirichlet过程无限混合模型[5～7]，如式(3)所示。

其中，p(xi|θsi)取正态分布。

2 参数估计

根据Bayesian理论:

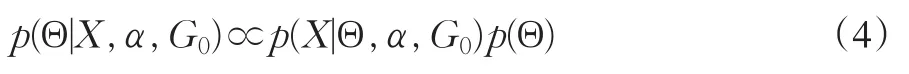
因此，式(3)中的未知参数的估计可通过计算其先验分布及似然函数来实现。本文首先确定各参数的先验分布，在此基础上确定各参数的满条件分布，最后通过MCMC方法估计出参数Θ。

2.1 Dirichlet过程先验分布

2.1.1 参数S和G的先验分布

（1）参数S的先验分布

可用于描述Dirichlet过程的模型有多种，本文基于经典的Blackwell-MacQueen Urn抽球模型，计算si的条件概率。其过程描述如下：某罐子中装有K种不同颜色的球。初始，罐中有红色球α1个，有黄色球α2个，…等，假设从罐中随机取出一个球（取N次），每次取完之后将两个相同颜色的球放回罐中。当趋近于无穷时，罐中各种颜色的球所占的比例α1,…,αK将遵循Dir(α1,…,αK)。若将该罐中球的颜色的种类K扩展到无限集，就得到Dirichlet过程[1,8,9]。即

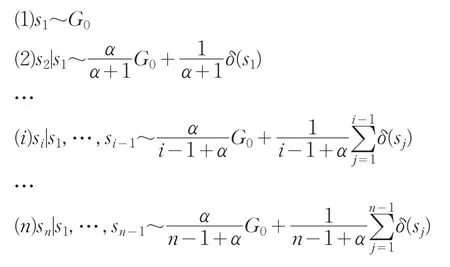
因此，Si的条件概率可采用式（5）计算。

其中，δsj(⋅)表示第j类中的样本个数。

（2）G的先验分布

G的先验分布，即（μk,）的先验分布。假设μk是p维均值向量，是p×p协方差矩阵。因为μk,（j=1,…,K）相互独立，在给定的条件下μk服从正态分布。即

服从p维Inverse Wishart分布，表示为

其中，δ表示形状参数，δ=n-p+1，n表示自由度；其均值为Q/(δ-2)。

因此，（μk,σ2k）的共轭先验分布为normal-inverse Wishart分布，所以G的先验分布即选择normal-inverse Wishart。

2.1.2 参数π的先验分布

π和（μ,σ2）相互独立，并且π的先验分布为Dirichlet分布：π～Dir(α1,…,αK)。

2.2 参数的满条件分布

本文利用Gibbs采样MCMC方法估计DNA基因表达数据的Dirichlet过程无限混合模型中的参数。由上述参数的先验分布，估计模型中各参数的满条件分布。

为描述方便，记

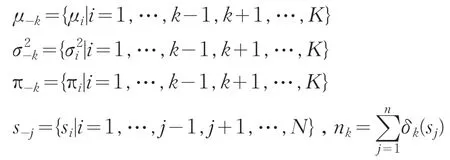
2.2.1μk的后验分布p(μk|μ-k,σ2,π,s,X)(k=1,…,K)

2.2.2的后验分布

2.2.3 πk的后验分布p(πk|π-k,μ,σ2,s,X)

若 给 定 s，则 π 与（μ,σ2,X）相互独立 ，所以p(πk|π-k,μ,σ2,s,X)=p(πk|π-k,s)∝p(π|s)。对于先验分布为Dirichlet分布而言，后验分布也一定是Dirichlet分布。因此

2.2.4si的后验分布p(si|s-i,μ,σ2,s,X)(i=1,…,N)

给定X和μ,σ2,π，si相互独立，所以p(si|s-i,μ,σ2,s,π

3 仿真结果与分析

为了验证本文所述算法的有效性，本文分别对仿真数据和IRIS测试数据集建立Dirichlet过程无限混合模型，展开聚类分析。

3.1 仿真数据

首先构造一组包含K=5个成分模型、N=400个样本的模拟数据集加以检验，该模拟数据集基于一个四维正态混合模型产生。其中，各成分模型的权重π={0.18,0.10,0.18,0.25,0.29}，对应的各成分正态成分模型的均值由正态先验分布随机产生：μ1={19.7,6.5,5.6,28.6}，μ2={1.2,7.2,21.6,20.6}，μ3={7.4,0.2,1.1,1.0}，μ4={24.9,26.4,14.8,4.6}，μ5={20.4,9.2,9.2,1.1}，对应的各成分正态混合模型的方差由InverseWishart分布随机产生：σ21={3.5,7.9,4.7,3.4}，σ22={6.4,4.8,4.7,1.7}，σ23={2.8,3.4,3.7,7.4}，σ24={9.0,6.1,4.8,2.7}，σ25={9.0,4.3,5.9,6.1}。

通过Dirichlet过程无限混合模型对模拟数据展开聚类分析，经过200次MCMC Gibbs采样，估计出模型中的各参数。采样过程中聚类个数K、Dirichlet过程的集中度参数α及聚类个数K的直方图如图1中所示。可以看出，对上述模拟数据，通过Dirichlet过程无限混合模型聚类分析估计出的数据中潜在的成分模型的个数，完全符合产生该模拟数据集的条件。

3.2 基因表达数据

图1 聚类个数K、集中度参数α及K直方图

本文以著名的白血病样本基因表达数据集作为测试数据集。该数据集于1999年由Golub收集，共包含72个急性白血病样本的7219个基因的表达水平，其中，急性淋巴瘤白血病（ALL）47例，急性骨髓瘤白血病（AML）25例。

对上述基因表达数据，同样建立Dirichlet过程无限混合模型进行聚类分析，并估计出模型中的各参数。采样过程中聚类个数K、Dirichlet过程的集中度参数α及聚类个数K的直方图如图2中所示。可以看出，对上述基因表达数据，通过建立Dirichlet过程无限混合模型聚类分析估计出的数据中潜在的成分模型的个数，也是符合该测试数据集的生物学描述的。

图2 聚类个数K、集中度参数α及K直方图

4 结论

本文提出建立Dirichlet过程无限混合模型进行DNA基因表达数据的聚类分析，该模型无需预先设定成分模型的个数，因而具有更好的灵活性和适应性，有利于我们挖掘数据中的各种有用信息。模拟测试数据集和Golub急性白血病DNA基因表达测试数据集的聚类分析结果表明了该方法在无监督聚类方法中的优越性。通过建立Dirichlet过程无限混合模型开展的聚类分析算法，能够正确地估计出DNA基因表达数据中隐含的成分模型的个数。

[1]Teh,Y.Dirichlet Process[EB/OL].http://www.gatsby.ucl.ac.uk/～ywtehe/search/npbayes/dp.pdf,2011.

[2]徐谦,周俊生,陈家骏.Dirichlet过程及其在自然语言处理中的应用[J].中文信息学报,2009，23(005).

[3]姚宗静.基于Dirichlet过程的非参数贝叶斯分析[D].西南交通大学,2007.

[4]Neal,R.Markov Chain Sampling Methods for Dirichlet Process Mix⁃ture Models[J].Journal of Computational and Graphical Statistics,2000,9(2).

[5]Gelman,A.,Carlin,J.,Stern,H.,Rubin,D.BayesianDataAnalysis[M].New York:CRC Press,2004.

[6]Kim,S.Mahlet G.Tadesse.Marina Vannucci.Bayesian Variable Selec⁃tion in Clustering Via dirichlet Process Mixture Models[J].Biometrika,2006,93(4).

[7]Dahl,D.Model-based Clustering for Expression Data Via a Dirichlet Process Mixture Model[J].Bayesian Inference for Gene Expression and Proteomics,2006.

[8]Teh,Y.,et al.Hierarchical Dirichlet Processes[J].Journal of the Ameri⁃can Statistical Association,2006,101(476).

[9]Rasmussen,C.,Z.Ghahramani.Infinite Mixtures of Gaussian Process Experts[C].Advances in Neural Information Processing Systems 14:Proceedings of the 2002 Conference,2002.