永磁风力发电机通风系统计算与热分析

刘丽红

(沈阳职业技术学院，辽宁沈阳110045)

0引 言

电机内的各种物理场是互相影响、互相制约的，且有一定耦合关系的综合场。电机内部的通风与温度场是通过对流换热的方式联系在一起的［1］。对于半直驱永磁风力发电机，由于其通常位于机舱内，自然冷却条件相对较差，需要采用附加的冷却措施。本文将对一台1 MW半直驱式永磁风力发电机通风系统进行计算分析。该永磁风力发电机通风系统的主要特点是:利用外加风机进行强迫风冷、并采用轴向式的通风结构;风力发电机定子铁心背部形成轴向通风道，圆周方向一共有24个彼此分离的风道;发电机一侧加鼓风机，驱动冷却流体沿轴向流动到另一侧，冷却电机各部件，然后从电机内排出，冷却空气与电机内的发热部件进行热交换，散去电机产生的热量。

由于电机结构的复杂性，电机内的通风系统很难精确计算。通风系统的工程算法是利用风路图来代替实际管道，根据实验结果或经验估计气体流动情况，做出风路图并计算系统中的各个风阻和合成风阻，从总体上计算出电机的风量和风速［2-3］。这种计算方法虽简单，但与实际情况差别较大，并且无法描述电机内部的实际风速分布状况和局部漩涡流动。随着计算机性能的不断提高，计算流体动力学已经渗透到许多相关学科和工程应用之中。同时，计算流体动力学(以下简称CFD)在电机通风冷却计算中已得到了应用。文献［4］采用二维流体场计算了大型发电机单个定子径向通风沟内的流体运动情况，在计算中忽略了流体流动在轴向的差异性。

本文采用CFD方法对发电机的通风系统进行三维流场计算，得到发电机内部的流量分配和风压降，以及发电机内部的风速分布，为发电机通风系统的优化设计提供了优越的平台。根据发电机内部的风速分布确定热计算的边界条件，采用等效热网络法计算得到发电机各部件的温升值。

1电机内流场的数学模型

电机内冷却空气的状态为定常粘性不可压缩湍流［5］。根据流体动力学理论，在直角坐标系中采用时均法，湍流流体流动控制方程包含时均连续方程和时均Navier-Stokes方程，其张量形式如下［6］:

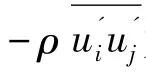
为使上述方程组封闭，通常需要引入新的湍流模型。其中，标准k-ε两方程模型在工程中使用最为广泛，它由湍动能k方程和耗散率ε方程构成。当流体为不可压且不考虑用户自定义的源项时，标准k-ε模型可描述:

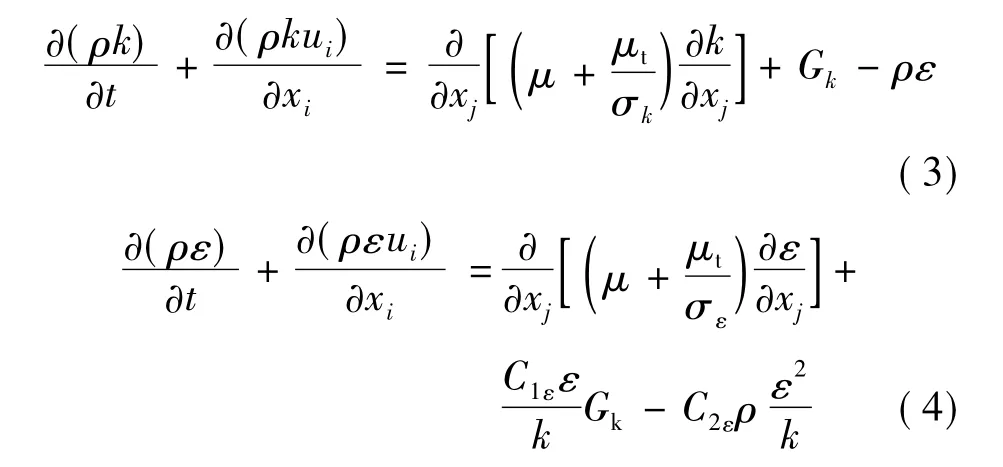
式中:μt为湍动粘度;Gk为由于平均速度梯度引起的湍动能 k 的产生项;C1ε、C2ε、σk以及 σε为常数。

2确定风机数目

本文采用基于CFD方法的Fluent 6．5软件对发电机内流体流动进行数值模拟，从而准确地计算出发电机内部的风速分布。实质上，Fluent软件只是一个求解器，它本身不具有建模和划分网格的功能。然而网格质量对CFD计算精度和计算效率影响很大，本文利用专用前处理软件GAMBIT来生成网格。冷却空气在电机内的流动状态为湍流，本文选取标准k-ε两方程模型来计算冷却空气的流动情况。对于近壁区域流体流动问题，采用壁面函数法来进行处理。在发电机的入风口设置速度入口边界条件来取代风机的作用，出风口采用压力出口边界条件。使用二阶迎风格式离散控制方程，选择压力速度耦合求解器进行求解。

由于发电机的外形尺寸比较大，为了使冷却空气均匀地进入电机内部，本文采用数台风机并联运行的方式。运用CFD方法计算发电机定子轴向通风道入口处的风速分布，根据发电机轴向通风道入口处风速分布的均匀度(最大风速与最小风速之差)确定风机的数量。由于6台风机在圆周方向上存在对称性，选取单个风机对应的发电机端腔区域作为计算区域。这里以6台风机为例来说明整个计算过程。图1为单个风机所对应发电机端腔内的风速分布图。从图中可以清晰地看出，冷却空气在端腔内的流动速度分布情况。图2为轴向通风道入口处的速度等值线图，从图中得到轴向通风道入口处的最大风速为20．3 m/s，最大风速发生在风机正对的通风道入口处。

图1 风速分布图

图2 风速等值线图

图3为选择6个风机时，单个风机所对应的4个轴向通风道入口处的风速分布情况。选择不同的风机数目分别计算，计算结果表明当选择6个风机并联运行时，各通风道内最大风速与最小风速之差百分比为14%;选择4个风机时，各通风道内最大风速与最小风速之差的百分比将超过20%。通风道内风速分布的不均匀会引起发电机温升分布不均匀。本文最终确定6台风机并联运行。

图3 通风道入口处风速分布

3通风系统计算

图4 静压等值线

在进行通风计算时，由于发电机的6台风机在圆周方向存在对称性，选取单个风机对应的发电机内冷却空气作为计算的求解区域进行建模，将模型对称面设置为周期性边界条件。图4为计算区域的静压等值线图。从图中可以看出，发电机的静压为1 080 Pa，发电机总压降为1 267 Pa。

图5为发电机求解区域的风速分布，通过观察风速分布图，发电机内的最大风速为32．8 m/s，最大风速位于发电机定子轴向通风道的入口处。冷却器空气的流速沿着轴向通风道方向逐步减小，但是变化幅度较小。

图5 风速分布图

通过以上计算得到通风系统总风压降为1 267 Pa，冷却空气流量为2．216 1 m3/s，为风机的选型提供了依据。根据计算结果，选择合适的风机对风力发电机进行冷却。

4热分析

发电机的温升计算需要确定发电机各部件的对流散热系数。本文根据上述CFD通风系统计算得到的发电机内部风速，确定各部件的对流散热系数。表1列出了发电机各部件的对流散热系数。

表1 对流散热系数

采用等效热网络法对发电机进行热计算，计算得到发电机各部件的温度分布如表2所示。由计算结果可以看出，发电机绕组沿轴向的温升分布是不均匀的，发电机的最高温升为78．8 K，位于靠近出风口侧的定子上层绕组处。

表2 计算结果

5结 语

本文采用CFD法对发电机进行了通风计算，确定采用6台外加风机对发电机进行冷却，计算出通风系统总风压降为1 267 Pa，冷却空气流量为2．216 1 m3/s，为风机的选型提供了依据。根据通风计算，确定热计算的边界条件，采用等效热网络法对发电机进行热计算，得到发电机各部件的温升值。由计算结果可以看出，发电机绕组沿轴向的温升分布是不均匀的，发电机的最高温升位于靠近出风口侧的上层绕组处，发电机的最高温升值为78．8 K，说明该通风系统能够满足温升要求。

［1］ 温嘉斌，孟大伟，周美兰，等．大型水轮发电机通风发热场模型研究及通风结构优化计算［J］．电工技术学报，2000，15(6):1-4．

［2］ 魏永田，孟大伟，温嘉斌．电机内热交换［M］．北京:机械工业出版社，1998:230．

［3］ 陈世坤．电机设计［M］．北京:机械工业出版社，2000．

［4］ 李伟力，丁树业，勒慧勇．基于耦合场的大型同步发电机定子温度场的数值计算［J］．中国电机工程学报，2005，25(13):129-134．

［5］ 王福军．计算流体动力学分析［M］．北京:清华大学出版社，2004．

［6］ Nerg J，Rilla M，Pyrhonen J．Thermal analysis of radial-flux electrical machines with a high power density［J］．IEEE Transaction on industrial electronics，2008，55(10):3543-3554．