基于区域极点配置理论的定子磁链全阶观测器

马艳洁

(沈阳职业技术学院，辽宁沈阳110045)

0引 言

定子磁链观测和速度估计一直以来都是高性能感应电动机无速度传感器直接转矩研究的热点。为了克服电机参数变化对磁链观测的不良影响，国内外学者进行了深入研究，取得了很多成果。文献［1］基于扩展龙伯格观测器的磁链观测方法，改善了控制系统的低速运行性能。文献［2］对定子磁链观测器的增益矩阵的确定方法进行了深入研究，取得了比较好的效果。为了克服定子电阻变化对磁链观测器和电机控制系统的不良影响，文献［3］设计了定子电阻辨识环节，提高了观测精度和系统性能，但是引入定子电阻辨识环节致使观测器结构复杂，应用性受到了限制，本文将在不增加系统复杂性的前提下，基于区域极点配置理论设计状态观测器的增益矩阵，提高观测精度和鲁棒性。

1感应电动机的状态方程

构建以定子电流和电子磁链定子磁链观测器，需要用到静止坐标系内的定、转子电压和磁链矢量方程如下:

式中:Rs、Rr和 Ls、Lr分别是定、转子电阻和定、转子电感;Lm是励磁电感;us是定子电压;ωr是转子角速度;is、ir和 ψs、ψr分别为定、转子电流和定、转子磁链。

综合式(1)～式(4)，可得电动机的状态方程:

在式(5)中，状态矩阵A包含了电感参数Lm和Lr、电阻参数Rs和Rr以及电机的转速ωr，电感参数值与磁路饱和程度有关，Rs和Rr受温度变化影响较大。将定、转子电阻、转速分别写成其标称值Rs0、Rr0、ωr0和其不确定项 ΔRs、ΔRr、Δωr相加的形式，可得:

式中:

设 ΔA 可以表示成 ΔA=EδF，其中，E∈Rn×s、F∈Rt×n是由于定、转子电阻和转速变化而引起的不确定性结构矩阵;不确定系数δ属于集合:

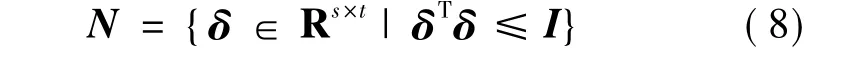
2定子磁链观测器的设计

考虑定子电阻、转子电阻不确定性以及运行过程中电机转速的变化，构建的状态观测器如下:

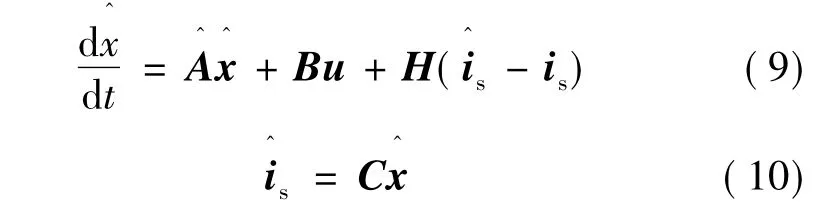
令状态误差为e，即:

由式(11)可得动态误差方程，即:

估计值与真实值x之间的衰减速度取决于观测器系统矩阵的A0+HC+EδF极点位置，亦即取决于观测增益阵H的构造。在构造H矩阵时，需注意在衰减的快速性与滤除噪声、防饱和效应之间进行折衷考虑。而如果精确配置矩阵A0+HC+EδF的极点，在指定极点位置的同时也限定了衰减速度和降低了鲁棒性，因此很难满足工程实际中所要求的多种性能指标。这样，为了使所设计的状态观测器具有更多的自由度，我们考虑基于区域极点配置的状态观测器的设计问题。

问题详细的叙述即是:构造具有一定自由度的观测增益阵H，使得对一切容许的不确定性F∈N，观测器系统矩阵A0+HC+EδF的极点(即状态估计误差系统式(12)的极点)都被配置在如图1所示的圆形区域D(a，r)内。我们称这样的观测器为D稳定鲁棒状态观测器。

(2) 对于套箍指标单参数变化试件，骨架曲线的改变显著，如图6(b)所示。套箍指标增大，钢管对核心混凝土的约束作用增强，使得试件承载力衰减缓慢，延性变好；而承载力的差异主要是由于柱截面或钢管截面的不同所致。

图1 区域极点配置示意图

定义 式(12)称作在观测器增益阵H下是二次可D镇定的(使系统D稳定)，当且仅当对一切容许的不确定性F∈N，存在对称正定阵P，使得:

由此，得到下面的结论。

定理1 设Q和R是两个适维的对称正定矩阵，不确定式(12)在观测器增益阵H下是二次可D镇定的充要条件是，存在ε＞0，使得下面的离散代数Riccati方程:

有对称正定解P，且满足:

定理的证明用到了矩阵逆定理、Schur complement、Finsler引理，详细的证明可参见文献［4］中的证明思路，限于篇幅文中不再详述。

为了便于求出观测增益阵H，我们把定理用线性矩阵不等式描述如下。

定理2 设R为适维对称正定阵，状态估计误差系统式(12)在观测增益阵H下二次可D镇定的充要条件是，存在ε＞0和对称正定矩阵P满足下面的线性矩阵不等式:

此时的观测器增益矩阵:

式(16)亦可将R当作变量，这样，观测增益阵就又有了一个自由度，以便用来优化其它控制指标。

3系统仿真及其分析

为了验证本文提出的基于区域极点配置磁链观测器设计方法的有效性，在Simulink下建立了直接转矩控制系统进行了仿真验证。算法中除了定子磁链观测器采用了文中提出的基于区域极点配置的定子磁链观测器外，其它部分都与传统的直接转矩控制一致，限于篇幅本文不一一介绍，详见参考文献［5］。仿真中所用电机参数:额定功率3 kW，额定电压380 V，额定电流6．8 A，额定频率50 Hz，极对数2，额定转速1 420 r/min，定子电感0．258 H，转子电感 0．258 H，互感 0．243 H，定子电阻 1．635 Ω，转子电阻 1．903 Ω，定子磁链 0．8 Wb。

为了验证所采用的定子磁链观测器在全速范围内都能比较准确地估计定子磁链和转速，分别对电机转速为50 r/min、1 420 r/min和电机转速在0．2 s时由1 000 r/min突变为500 r/min三种情况作了仿真研究。电机的定、转子电阻处于标称状态时，观测器的观测效果较理想，限于文章篇幅不再给出仿真结果，为了体现观测器的鲁棒性，仿真过程中将电机的定、转子电阻都设置为其标称值的1．5倍。

从仿真图2～图4可以看出，本文提出的基于区域极点配置理论的定子磁链观测器在高速、低速还是转速突变时都能很好地观测定子磁链，表明该观测器对电机的电阻变化和转速变化都较强的鲁棒性。

图2 转速50 r/min时的仿真结果

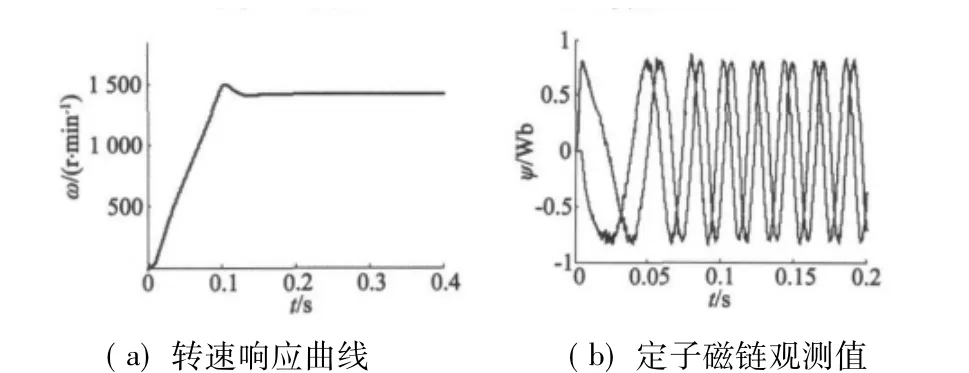
图3 转速1 420 r/min时的仿真结果

图4 转速突变时的仿真结果

4结 语

本文以感应电动机的定子电流和定子磁链为状态变量，建立了同时考虑定、转子电阻不确定性以及运行中速度变化的定子磁链观测器，基于区域极点配置理论设计了观测器的增益矩阵。从仿真结果可以看出，本文提出的基于区域极点配置的定子磁链观测器具有较强的鲁棒性，在定、转子电阻变化很大以及转速突变时仍能较准确地观测定子磁链和转速。

［1］ Choi Y O，Lee K Y，Seo K S，et al．Performance analysis of the DTC using a closed loops stator flux observer for induction motor in the low speed range［C］//Proceedings of International Conference on Electrical Machines and Systems．Shenyang China，2001(1):89-93．

［2］ 奚国华，高宏洋，许为，等．定子磁链全阶观测器增益矩阵的确定方法［J］．中南大学学报(自然科学版)，2008，39(4):793-798．

［3］ Nian Xiaohong，Wang Tao，Wang Jian．et al．Adaptive stator resistance estimation method for speed sensorless DTC controlled IM drives［C］//Proceedings of Applied Power Electronics Conference and Exposition．Anaheim，CA，United states，2007:214-221．

［4］ 刘满．基于区域极点配置的若干控制问题的研究［D］．沈阳:东北大学，2005．

［5］ 王成元，夏加宽，孙宜标．现代电机控制技术［M］．北京:机械工业出版社，2009．