潘家窑煤矿原副斜井涌水问题数值模拟研究
2012-07-20刘志鹏
刘志鹏
(山西省水利水电科学研究院 山西太原 030002)
1 研究区概况
1.1 研究区斜井涌水概况
本次研究的对象为潘家窑煤矿整合前的原崔家岭矿副斜井涌水问题,研究区范围选取潘家窑煤矿的东部原崔家岭矿副斜井周围一定范围。据现场调查,潘家窑煤矿原崔家岭矿副斜井内距井口约60 m处有三股地下水涌出,进入斜井内,其中两股涌水点位于斜井壁脚处,标高分别为1 233.34 m和1 230.29 m,分别距井口61.0 m和68.8 m,另一股位于斜井壁顶部,距井口68 m,三处涌水点涌水量分别为13.17 m3/h、40.71 m3/h和4.20 m3/h,总涌水量为58.08 m3/h。
1.2 研究区范围及深度的确定
潘家窑煤矿原副斜井位于上窑村七里河谷,副斜井涌水补给属浅层地下水补给。据查,浅层地下水的补给来源主要为附近的地表水和大气降水,本次研究工作的具体范围是:北部、东部以七里河为界,西部、南部考虑地下水影响到涌水点的距离,分别距涌水点126 m和200 m,研究区范围总面积0.152 km2。
副斜井涌水点出露处的位置埋深约29.77~32.82 m,岩性为二叠系下石盒子组砂岩,其下为泥岩,即涌水出露点位置为砂岩与泥岩接触带附近,下石盒子组泥岩为浅层地下水的隔水层,故本次研究深度范围为地表至二叠系下石盒子组泥岩,上部为孔隙潜水,下部为裂隙水,两者之间没有隔水层,具有统一的水力联系,泥岩为隔水层。
1.3 水库概况
七里河水库位于七里河上游安家岭矿附近干流上,研究区东南部,距潘家窑煤矿原副斜井约200 m。为小II型水库,工程等级为V等。库坝为土坝,坝顶高程为1 252.0 m。中隔墙将库区分为两区,右侧行洪河槽总长为852.42 m,高程由1 247.0 m降至泄洪闸进口底板高程1239.0m,左侧为蓄清区,面积约5.7万m2,高程由1 243.8 m降至1 239.0 m。
2 研究区水文地质结构及涌水来源、补给途径分析
2.1 研究区水文地质结构
研究区浅层地下水含水层从岩性上来分有两层:即第四系砂卵石层和二叠系砂岩,前者赋存孔隙水,后者赋存裂隙水。两者之间没有或只有局部隔水层,因而孔隙水和裂隙水具有统一的水力联系。砂岩下伏泥岩为隔水层,是以上含水层的隔水底板。含水层、隔水层共同构成研究区浅层地下水储水结构,虽然地下水含水介质不同,但它们具有统一的水力联系,从埋藏条件来分它们属于潜水类型。研究区浅层地下水具有统一的补给来源,主要来源于七里河水的下渗补给、大气降水的入渗补给以及调蓄水库高水位时水库的渗漏补给等。
研究区北部、东南部为该浅层地下水的补给边界,由于七里河上游截流后无大的洪水流经,而平时各种排水基本常年不变,该补给边界可按定水头对待。地下水补给后向西南方向径流,为流量边界。
2.2 副斜井涌水来源、补给途径分析
大气降水和河水渗入地下后首先补给第四系松散层孔隙水,然后随地下水径流。其下伏砂岩由于存在裂隙,特别是构造裂隙,孔隙水可以下渗进入砂岩裂隙中,使裂隙水获得补充,随统一的径流场流动。由于研究区副斜井的掘进,正好通过砂岩中裂隙发育带,而副斜井通过浅层地下水底板掘进至煤层,故砂岩裂隙中的地下水就进入到副斜井中,形成涌水。由于砂岩裂隙的导水性较强,于是在裂隙发育带和副斜井涌水点一带形成强径流带,地下水除顺裂隙向西南方向径流外,很大部分水量涌入到副斜井中。
七里河水库渗漏可能进入副斜井的途径与以上类似,为水库水渗漏进入第四系松散层,然后随地下水径流通过导水裂隙进入副斜井中。
3 矿井涌水数值模拟研究
3.1 水文地质条件的概化
边界条件表示的是研究区域的地下水系统与其周围边界环境之间的关系,周围环境的变化对研究系统有影响[1]。模拟区范围,东部和北部以七里河及水库库岸为界,西北部、西部和南部为人为边界,研究区东西长约330 m,南北宽约445 m,面积约为118 145 m2。
根据区内水文地质钻孔资料及地下水存储条件,将模拟区内含水层概化为一层。在对基本条件进行系统分析的基础之上,借鉴前人的工作成果进行参数分区,统一参数分区内含水层可视为均质,水流服从达西定律。根据区内的地质、水文地质条件,结合水动力场特征,将七里河及水库边界概化为第一类边界,其他边界概化为第二类边界,其中七里河及水库库岸为补给边界,其余边界为排泄边界。整个地下水流态概化为三维非稳定流,四周均按通用水头边界处理,系统的底部为隔水边界。根据实际长期观测的系列资料,选择模拟时段为2010年9月5日至2010年9月30日,以2010年9月5日的水头分布作为研究区的初始水位。
3.2 地下水系统数学模型的求解原理与方法
3.2.1 求解原理
建立地下水水流模型之后,运用Visual Modflow软件模拟地下水流场时,首先要对研究区进行离散化处理,下面将通过对含水层的离散化处理来说明水流模型的求解原理。
首先对含水层进行空间离散,即网格剖分。将一个三维含水层系统划分为一个三维的网格系统,整个实际含水层被划分为若干层,每一层又剖分为若干行和若干列。这样,含水层被剖分成若干个长方体,称为计算单元格,每个计算单元格的位置用该计算单元格所在的行号(i),列号(j)和层号(k)来表示。每个剖分出来的小长方体的中心称为节点,一个计算单元格的水头由水头在该节点的值所表示[2]。
其次对时间进行离散。时间可以根据实际情况分为若干个应力期。在每个应力期内,所有外部源汇项(如抽水量、入渗量等)的强度保持不变。每个应力期又可以再分为若干个时段,每个时段内的时间步长可根据实际变化情况选择。
对于计算单元格,从地下水流动的连续性方程出发,根据流入和流出计算单元格的水流量之差等于单元格中贮水量的变化的水均衡原理,导出其六个界面上的有限差分公式,同时考虑外部源汇项对其影响,获得计算单元格的地下水渗流计算有限差分公式。依次列出所有有效单元格的向后差分格式,这些方程构成了一个线性代数方程组。利用初始条件对其进行迭代求解,就可以获得每一个时段末地下水位的平面分布。
3.2.2 求解方法
由于所计算的水头值,既是空间坐标的函数,也是时间坐标的函数,因此不仅要将数学模型进行空间上的离散化,同时也要进行时间的离散化。
地下水运动的有限差分公式实际上是根据地下水流动的连续性方程进行的。按照连续性方程,流入和流出某个计算单元的水量之差应等于该单元格中贮水量的变化。当不考虑地下水密度的变化时,连续性方程可简单的表示为:
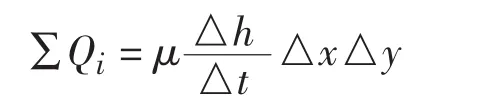
式中:∑Qi——单位时间内流进或流出该计算单元的水量

μ——含水层的给水度(无量纲);
△x,△y——计算单元的空间间距(L);
△h——某一时间段内水头的变化(L);
△t——时间步长(T)。
若考虑垂向水量交换,对某个计算单元(i,j)而言,其垂向水量增量可以用下式表示:

式中:Wij——流入计算单元(i,j)的水量(L3/T);
ε1i,j——垂向入渗补给量(L3/T);
ε2i,j——垂向排泄量(L3/T)。
将模拟区每个计算网格的水头hi,j进行表示,可得到n个线性方程,将它们组成一个n维的线性方程组,用矩阵表示为:
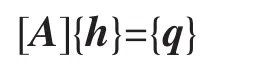
式中:[A]——水头的系数矩阵;
{h}——所求的水头矩阵;
{q}——表示各个方程中所包含的常数项和已知项,也称右端项。
在Visual Modflow中,系数矩阵和右端项是通过各个软件包来逐步计算的,最后通过迭代法即可求得水头矩阵的系列解。
3.3 模型的设计与实现
3.3.1 计算区剖分
将研究区在平面上剖分为80行,80列,其网格为矩形,共计6 400个单元格,每个单元格的平面面积约为22.9 m2。
3.3.2 定解条件的确定
根据2010年9月5日研究区内长观孔的监测资料,经过差值计算求得含水层的渗流场,将其作为研究区的初始流场,见图1。

图1 初始流场图
3.3.3 地下水均衡要素的确定
在处理地下水系统的源汇项时,包括补给项和排泄项两项内容。在均衡区内,地下水补给项主要包括大气降水入渗补给、地下水侧向径流补给和河道渗漏补给;地下水排泄项主要包括潜水蒸发和径流排泄。计算研究区内各均衡要素的目的在于确定地下水的各个补给排泄随时间和空间的变化规律,为建立地下水数值模拟模型准备数据。
建立涌水量预测模型时涉及的主要参数为单元的渗透系数K、给水度μ、储水系数S和孔隙比。其中最为关键的是渗透系数K以及储水系数S。由于受构造及水文地质条件的影响,这些参数在空间上表现出较强的差异性,因此有必要先进行参数分区[3]。渗透系数分区主要是根据已知资料和某些已知点以及区域水文地质条件确定的,分区的取值受人为因素影响比较大[4]。水文地质参数分区原则上需综合考虑以下要素:含水层的富水性规律和补径排条件、断裂构造的特点以及观测孔的数量和分布[5]。
最后,运用Visual Modflow软件进行地下水的数值模拟,输入或修改各类水文地质参数和几何参数,运行模型,反演校正参数,直到显示输出结果。
3.4 模型的识别与验证
本文运用了试错法对模型参数进行确定,经过反复调参,得到较为合理的模型识别结果和合理的参数组合。模型识别的过程实际上是反求参数以使其与水文地质原型相仿真的过程[6、7]。
3.4.1模型的识别
根据研究区地下水位观测资料的实际情况,选取2010年9月5日至2010年9月30日作为模型识别阶段,以五天作为一个步长,分六个步长来计算研究区内的水位。依据含水层的岩性、导水性和埋藏条件、厚度以及水位动态特征,按照不同的水文地质条件将研究区分为六个参数区,见图2,具体分区方法本文不再赘述。
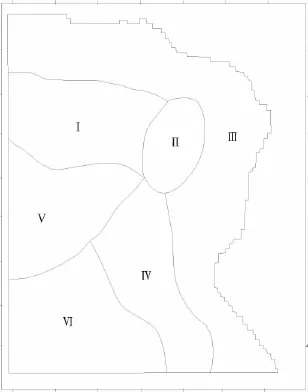
图2 参数分区图
将计算值与已有资料的观测值比较,进行水位拟合。尽管观测区内的观测点较多,但是因部分观测点的观测资料不全,本次试验只选用两个代表性水位观测孔SK10及SK7进行水位拟合,拟合曲线见图3、图4。

图3 SK10孔水位拟合曲线图
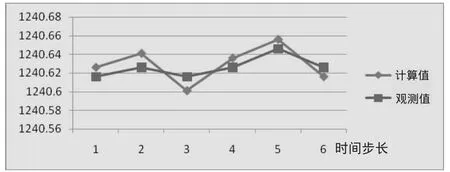
图4 SK7孔水位拟合曲线图
由图3、4可知,本次识别各时段观测孔水位计算值与实测值的拟合误差符合模型误差要求,模拟的结果表明系统稳定性较好,模拟的精度和效果是理想的,建立的研究区水文地质模型是比较符合实际的。
3.4.2 模型的验证
为进一步验证识别后的模型和水文地质参数的可靠性,对模型进行验证,用校正后的模型及参数组合计算出各观测点的水位,将计算结果与实测水位比较。根据计算区地下水位观测资料的实际情况,选择2010年10月5日至2010年10月25日期间的水位观测资料对模型进行验证。模型的结果见图5、6,可知本次验证各时段水位拟合误差符合验证要求。
综上,模拟结果表明通过水文地质条件的概化、边界条件的确定、源汇项的处理、水文地质参数的选取以及参数调整后所建模型能够较好地反映研究区的水文地质特征,且误差均在工程允许范围之内,所以该模型可以用于地下水位动态预报。

图5 SK10计算结果与实测值对比图
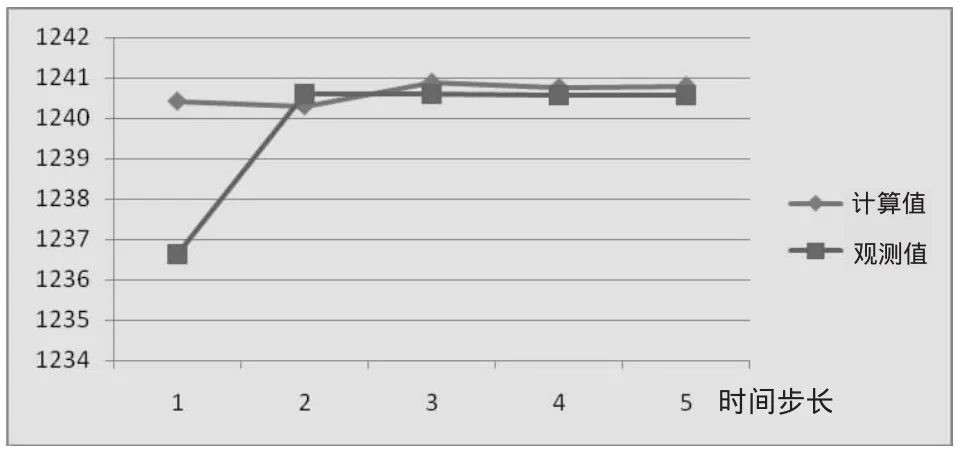
图6 SK7计算结果与实测值对比图
4 模型结果
本次模拟计算将研究区作为一个水文地质系统,计算的目的层为浅层地下水,包含二叠系下石盒子组砂岩裂隙水及第四系松散层孔隙水,概化为非均质各向异性。整个地下水流态概化为平面非稳定流,四周均按通用水头边界处理,系统的底部为隔水边界。通过模型运转,按水库高水位和低水位,能够预测水库渗漏对副斜井涌水的影响。
在水库不同蓄水水位条件下,研究区的侧向补给量随着水库蓄水水位的升高和降低而增大和减少。目前水库水位为1 245.1 m,属一般高水位,据调查,水库平时蓄水高度也在此高程附近,前面模型建立和验证时即按此作为初始水位。而水库库底高程为1 240 m左右,水库设计高水位为1 250 m,故本次工作模拟预测水库蓄水在1 240 m和1 250 m时对研究区地下水水位的影响。通过模型运行,得出研究区渗流场,其流场模拟结果如图7、图8所示,具体运算过程本文不做详细叙述。
通过数值模拟可以看出,水库渗漏对副斜井涌水有一定的影响,但其影响程度有限。目前库水位为1245m,副斜井涌水量为58.083 m3/h;当库水位为1 240 m时,基本上为空库,这时不会产生渗漏,副斜井涌水量为49.125 m3/h;当库水位为1 250 m时,副斜井涌水量增加为66.25m3/h,水库渗漏对副斜井产生了影响。

图7 水库蓄水在1240m时渗流场模拟结果
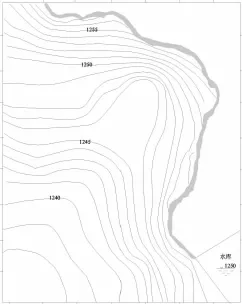
图8 水库蓄水在1250m时渗流场模拟结果
[1]薛禹群.地下水动力学[M].北京:地质出版社,1997.
[2]武强,董东林等.水资源评价的可视化专业软件(Visual Modflow)与应用潜力[J].水文地质工程地质,1999,26(5):21-23.
[3]宋西平,寇广潮.地下水数值模拟面参数和水文参数研究的重要性[J].地下水,2001,23(2):63-64.
[4]魏加华,陈良程,张远东等.地下水数值模型三维可视化研究[J].煤田地质与勘探,2003,31(4):33-36.
[5]郑红梅,刘明柱.Visual modflow在天津市地下水数值模拟中的应用[J].华北水利水电学院学报,2007,28(2):8-1l.
[6]陈崇希.“防止模拟失真,提高仿真性”是数值模拟的核心[J].水文地质工程地,2003,47(2):1-5.
[7]蒋玲.和县龙塘沿铁矿矿坑涌水量预测研究[D].合肥:合肥工业大学,2009.
