基于电流反馈的MSCMG轴向磁轴承低功耗控制

陈建仔，周向阳，魏彤，任元

(1.惯性技术国防科技重点实验室，北京 100191；2.新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191)

控制力矩陀螺(CMG)是大型卫星、空间站等长期运行的大型航天器实现姿态控制的关键执行机构。航天器姿态控制系统对CMG的基本要求是寿命长、体积小、质量轻、功耗低。根据陀螺转子的支承方式, CMG可以分为机械轴承支承和磁轴承支承[1]。早期CMG高速转子采用机械轴承支承，但是磨损和振动严重影响了CMG的精度和寿命。与机械轴承相比，磁轴承具有无接触、无需润滑、高转速、低功耗、长寿命、高精度及对振动可实现主动控制等优点[2]，因而，磁悬浮控制力矩陀螺(MSCMG)是大型航天器实现高精度、长寿命和快速姿态机动的有效途径。

功耗是MSCMG的一项重要指标，也是影响MSCMG空间应用的主要因素，低功耗是航天器不断追求的目标。磁轴承功耗包括铁耗和铜耗，磁轴承线圈由于通电而产生的铜耗是其功耗的主要部分。传统全主动磁轴承线圈中的电流包括偏置电流和控制电流。MSCMG采用永磁偏置混合磁轴承，利用永磁体替代偏置电流以产生偏置磁场，大大降低了静浮的功耗[3-4]。主动磁悬浮轴承的控制方式是通过检测磁悬浮轴承的间隙变化，控制线圈电流，提供相应的电磁力平衡负载，实现稳定悬浮。因此，轴承负载越大，需要的电磁力就越大，从而电磁铁线圈的控制电流就越大，功耗也就越大。因此，要进一步降低永磁偏置混合磁轴承的功耗，就需要减小其稳态悬浮电流。

文献[5]在基于磁轴承-转子系统动力学模型的基础上，提出了一种根据输出力矩变化调节径向轴承转子悬浮位置的角速率-转子位移前馈控制方法，降低MSCMG输出力矩时径向磁轴承的支承功耗。而这种参考框架角速度的低功耗方法只对径向通道进行控制，不适合用于轴向磁轴承的低功耗控制。

文献[6-7]给出了单自由度磁悬浮支承的零功率控制，采用的方法是电流积分小闭环反馈控制，使支承机构处于稳态时几乎不消耗能量，但是这种控制方法只适用于PD控制，而不适用于其他控制器，因此不便于控制器的选取和优化设计。

为了进一步降低MSCMG轴向永磁偏置混合磁轴承的功耗并克服传统低功耗控制方法的不足，在建立系统数学模型的基础上针对传统定气隙控制时线圈电流随负载增加而加大的问题，在分析传统低功耗控制方法的机理基础上，提出一种基于电流积分正反馈的轴向混合磁轴承-转子系统变气隙低功耗控制方法，该方法不仅可以实现低功耗控制，而且方便了控制器的设计。最后对所提出的控制方法进行了仿真及试验验证。

1 MSCMG轴向磁轴承系统建模

在轴向磁轴承控制中，一般采用差动驱动模式驱动电磁铁，如图1所示，同时获得一对方向相反的磁作用力[8]。在这种差动激磁方式下，一个磁铁以偏置电流I0与控制电流Ix之和激磁，而另一个磁铁则以Ix-I0激磁，采用永磁偏置的磁轴承的偏置电流I0为转子在平衡位置时的永磁体等效线圈电流。于是在这一对磁极间产生的合力f为

图1 轴向磁轴承的差动工作方式

(1)

式中：f+和f-分别为两个磁铁的作用力；x0为气隙大小；x为偏移磁中心的距离；K=μ0s0n2/4；μ0为真空中的磁导率；s0为气隙面积；n为单个电磁铁的线圈匝数。

在平衡点附近，对(1)式线性化，可表示为

f=khx+kiix,

(2)

(3)

式中：X(s),I(s)分别为磁轴承位移x和电流i的拉氏变换；m为转子质量。由(3)式可知，系统存在一个位于正实部半区的极点，自身开环不稳定，因此为使转子能稳定悬浮必须进行主动控制[9]。

闭环磁悬浮转子系统由位移传感器、控制器、功放、电磁铁和转子构成[10]。轴向通道广义被控对象系统框图如图2所示。

图2 轴向磁轴承转子系统框图

功放电路通常可用一阶低通滤波器线性模型来近似，其作用是将控制器输出的控制量i*转换为控制电流i，kw是功放放大倍数，截止频率为1/τa。所以，功放传递函数可表示为

(4)

位移传感器由于带宽很高，远超过需要主动控制的频率(10倍以上)，故可直接用比例环节描述

us=ksxs，

(5)

式中：us为传感器输出电压；ks为传感器灵敏度；xs为转子输出的位置坐标。

控制器一般使用PID控制或PD控制，PID控制传递函数gc(s)=Kp+Tis-1+Tds, 其中Kp，Ti，Td为控制器PID各项系数。由于在PID控制中，纯微分环节对噪声敏感，容易引起控制过程振荡，导致调节品质下降，所以采用不完全微分，截止频率为1/Tf，即gc(s)=Kp+Tis-1+Tds(1+Tfs)-1。

加入主动控制后的闭环磁悬浮转子系统闭环传递函数为

(6)

2 电流积分正反馈-转子变气隙控制

在采用定气隙控制时，参考位置不变，假设此时参考位置u0=0，闭环转子系统当受到干扰力fd作用时，由于加入PID控制，磁悬浮转子能稳定悬浮在参考位置。当x=0时，根据(3)式，此时功放电流增加为

(7)

传统的低功耗控制使用的是电流积分小闭环反馈控制，系统框图如图3所示。采用这种低功耗控制方法时，控制器只能选用PD控制[6-7]，即gc(s)=Kp+Tds，而当系统为了减小稳态误差选用PID控制时这种方法将失去作用。

图3 传统的磁轴承低功耗控制系统框图

而基于电流积分正反馈-转子变气隙控制不仅可以选用PD控制器，还可以选用PID或其他控制器。加入低功耗控制器gl(s)后的系统框图如图4所示。电流正反馈传递函数gl(s)=klis-1为积分控制器,kli为电流积分系数。通过电流积分正反馈，将反馈量输出到参考位置，改变转子悬浮参考位置使永磁体提供主要承载力，从而减小磁轴承线圈电流。

图4 磁轴承转子变气隙控制系统框图

以承载力fd为输入，控制电流i为输出的传递函数为

(8)

设fd为恒定负载P，进行拉氏变换fd(s)=Ps-1，则输出的控制电流i的拉氏变换为

(9)

当采用PID或PD控制器时，承载力fd≤kxxmax，其中xmax为轴向轴承气隙，由于gl(s)=klis-1(kli≠0)的作用，可以计算得到

(10)

根据拉氏变换的终值定理，由(10)式可以得到

(11)

因此采用这种控制方法可以使悬浮电流为零，从而达到降低功耗的目的。

图5为加入gl(s)与不加入gl(s)，以负载fd为输入，控制电流i为输出的bode图。从图中可以看出，加入gl(s)后，控制电流i对低频干扰fd的响应有很大衰减。如bode图中0.1 Hz处，在加入gl(s)后，幅值由-56.6 dB衰减到-83.5 dB，可以推出fd为静态承载力时，加入电流积分正反馈gl(s)能有效减小线圈电流。

图5 fd为输入，控制电流i为输出的bode图

使用电流积分正反馈-转子变气隙控制方法降低功耗的物理解释是：磁轴承承载力由永磁体和控制电流同时提供，因而通过检测电流变化，调节磁悬浮转子的悬浮位置，使永磁体提供主要的承载力，即可减小控制电流，进而降低磁轴承的功耗。

3 仿真分析

3.1 仿真条件

针对上节的分析，建立系统的仿真模型，下面基于Simulink分别对上述变气隙低功耗控制方法展开仿真分析。结合实际系统的设计参数，模型仿真参数见表1。

表1 模型仿真参数

3.2 加入gl(s)后的系统稳定性分析

从理论上讲，加入积分控制可以消除系统静差，gl(s)的积分增益参数kli是使电流稳态趋于零的速度度量，因此调整kli是降低功耗的主要手段。根据闭环系统的极点分布判定基于电流积分正反馈的变气隙磁轴承低功耗控制是否稳定，由图4可知，加入gl(s)后轴向磁轴承系统闭环传递函数为

(12)

图6为系统闭环零极点分布，kli从0到240，步长为10绘制。从中可以看出，kli使系统增加了一个位于原点的零点，可以计算出当kli<216.8时系统闭环极点均位于左半平面，系统稳定。

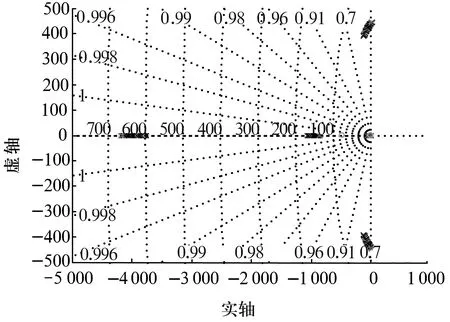
图6 系统闭环零极点分布图

结合上面的仿真参数，分别对不同电流积分系数kli的情况进行对比仿真，得到如图7所示的电流及转子悬浮位置变化波形。从图7可知，电流积分系数kli变大，系统电流及转子悬浮位置调节时间减小，电流超调量将增大，在kli=150出现电流波动。因此在系统响应速度满足应用条件的情况下，电流积分系数kli不宜过大。

图7 不同电流积分系数对控制电流及转子悬浮位置的影响

3.3 轴向磁轴承的位移、电流仿真

由上节分析得出，电流积分系数kli不宜过大，下面以选取kli=80为例，对轴向磁轴承的位移、电流进行仿真。轴向磁轴承通道电流积分正反馈-转子变气隙控制的位移、电流仿真结果如图8所示。

图8 变气隙控制的转子悬浮位置与线圈电流仿真

未采用电流积分正反馈变气隙控制(kli=0)时，在t=1 s，加入阶跃干扰力fd=50 N，传感器测得的转子位移在零值附近变化，最后稳定在零值。而轴向磁轴承的控制电流增加，最后稳定在0.073 A，此时承载力主要由控制电流产生。而当采用电流积分正反馈的变气隙控制后(kli=80)，对于阶跃干扰力fd，传感器测得的转子位移迅速发生变化，转子偏离了平衡点的位置，最后转子稳定到52.6 μm处。而控制电流首先有个增大的过程，由于电流积分正反馈的作用，电流迅速减小，趋于稳态至零，此时承载力全部由位移负刚度提供。

4 试验验证

为了验证电流积分正反馈的变气隙控制方法降低磁轴承功耗的有效性，利用图9所示的磁悬浮转子的单框架控制力矩陀螺试验系统平台进行试验。

图9 磁悬浮控制力矩陀螺样机

试验中，通过陀螺框架的转动，使转子轴向偏离水平方向，从而将转子本身重力在轴向的投影分量作为干扰力作用在轴承上，干扰力为50 N。

试验结果如图10所示，图10a中不加入电流反馈gl(s)，转子保持在稳定悬浮位置0 μm处，加入干扰后，线圈控制电流增加至0.063 A。试验中采用28 V控制电压,则此时轴向磁轴承静浮铜耗增加为1.764 W。图10b为加入电流反馈gl(s)后的试验效果，从图中可以看出，当受到干扰力时，转子悬浮位置自动发生变化，稳态时转子悬浮在59 μm附近，而控制电流由0.005 A在小的振动后又迅速恢复到0.005 A，稳定后可以看出受到50 N干扰力时，线圈电流没有额外的增加，轴向磁轴承静浮铜耗为0.14 W。试验中控制电流没有达到零，这是由于测量的电流采样电路的零点偏移误差造成的。可见，与传统的定气隙控制相比，在负载为50 N时，基于电流积分正反馈的变气隙控制能有效降低90%以上的铜耗。显然，在其他负载条件下，该控制方法同样有效。

图10 转子悬浮位置和线圈控制电流的试验效果

5 结束语

针对MSCMG轴向磁轴承的低功耗控制，提出了采用电流积分正反馈的转子变气隙控制方法，对算法进行了推导，并对主要参数进行了讨论和设计。仿真和试验结果表明，当负载存在时，该方法能大大降低永磁偏置磁轴承的铜耗。该方法不仅具有良好的稳定性，而且方便了控制器的设计，克服了传统低功耗控制方法的不足，并提高了可靠性，因此具有广泛的应用前景。