基于第2代小波和Hilbert-Huang变换的轴承故障诊断

刘小丽，张晓光，陈莹莹

(中国矿业大学 机电工程学院，江苏 徐州 221116)

在滚动轴承运转过程中，由于设备运行不稳定、载荷变化等多种因素，所采集的振动信号往往伴随着大量噪声，且有用信号易被噪声淹没，造成信号分析的不准确[1]。因此，为获得正确的信息，须对振动信号进行消噪。传统的消噪方法效率低且信息获取不全，第2代小波变换是一种柔性的变换方法，其不再依赖于有限的几种小波基函数，可采用插值细分法构造新的小波，所有的运算均在时域进行，具有原理清晰、算法效率高等优势[2]。而在第2代小波基础上发展的自适应冗余第2代小波解决了其变换引起的频率折叠问题，具有自适应性，特性更为良好。

当轴承零件出现故障时，其信号通常表现为非平稳的冲击特性，激发零部件的高频固有频率[3]。而常用的Fourier变换、小波分析等信号分析方法具有如窗口不可调、波基难选择等局限性，不适于非线性分析。Hilbert-Huang变换(HHT)是基于数据本身的自适应基函数，适合非线性、非平稳信号的分析处理，具有自适应性、人为因素低、时频分辨率高及时频聚集性良好等独特优点[4]。

将第2代小波与HHT算法结合，对轴承振动信号进行消噪、分析及故障特征提取，原理清晰化的同时提高了算法效率，仿真试验结果表明，该法不仅可以有效地去除噪声，而且能够很好地提取信号的局部特征。

1 第2代小波原理[3，5]及Hilbert-Huang变换

1.1 第2代小波

基于插值细分方法的第2代小波变换可分为分解与重构两部分，其中分解过程由分裂、预测与更新3部分组成。

设信号序列为X={xk,k∈R}，分裂是将信号分解为偶数样本序列Xe和奇数样本序列Xo，

(1)

预测是用相邻的偶数样本Xe和预测器P来估计奇数样本Xo，则可得预测误差

d=Xo-P(Xe)。

(2)

在第2代小波理论中，预测误差d即为小波系数，对应于高频分量。

更新使得子样本维持原始数据的某些整体特性，具体过程为由预测误差d通过更新器U与偶数样本序列Xe叠加来计算近似样本序列，

C=Xe+U(d) 。

(3)

C是对信号的一个粗略近似。第2代小波变换通过使用线性、非线性或空间变化的预测器和更新器而具有可逆性，算法简单，更适于自适应、非线性变换。

重构过程为分解的逆过程，包括恢复更新、恢复预测与合成3个部分，最终由奇偶样本序列合并构成重构信号。

1.2 自适应冗余第2代小波

第2代小波变换中，分裂与合成操作会导致信号的频率折叠，且更新在预测之后进行易导致更新器的计算趋于复杂。冗余第2代小波变换不再进行分裂与合成操作，不同分解层上的冗余预测器和冗余更新器通过插值运算构造，能够直接对逼近信号进行对称预测和更新。将冗余第2代小波与先更新后预测的第2代小波变换法结合可得到自适应冗余第2代小波变换[6]，具有更好的自适应性，较好地保留了信号的时域特征。

1.3 Hilbert-Huang变换

HHT包括EMD分解和Hilbert变换。EMD将信号分解为若干个IMF分量，然后对每个IMF分量进行Hilbert变换得到Hilbert谱或边际谱，从而实现HHT。

Hilbert边际谱反映了信号幅值随频率的变化情况，比Fourier谱具有更高的频率分辨率。而针对感兴趣的IMF分量进行Hilbert变换，求出瞬时频率和瞬时幅值，将其组合可得到局部Hilbert谱[4，7]。

2 自适应冗余第2代小波构造及其仿真试验

采用小波变换对信号进行消噪一般先要确定分解层数；然后对信号进行分解，对分解后各尺度下的细节系数进行阈值处理，最后将处理后的各层细节系数与最后一层的近似系数进行重构，获得消噪后的信号[8]。

利用MATLAB进行仿真试验，分别利用小波变换和自适应冗余第2代小波对MATLAB中的仿真信号noisbump信号进行消噪。其中，小波消噪使用sym8小波，heursure软阈值处理，降噪层数为2；自适应冗余第2代小波的初始更新器长度为4，初始预测器可选长度为{2,4,6,8}，选取消噪阈值为3.5，分解层数为2，并采用软阈值方法处理分解后的细节系数。仿真消噪结果如图1和图2所示。其中，图1为小波变换的消噪结果，均方误差值为4.7770，信噪比为14.8954；图2为自适应冗余第2代小波的消噪结果，均方误差值为0.811 1，信噪比为15.297 9。分析可见采用自适应冗余第2代小波消噪后的信号更加平滑，误差信号分布也较为均匀，所得信噪比高于小波消噪所得信噪比，而均方误差则大大小于前者误差，消噪效果更明显。

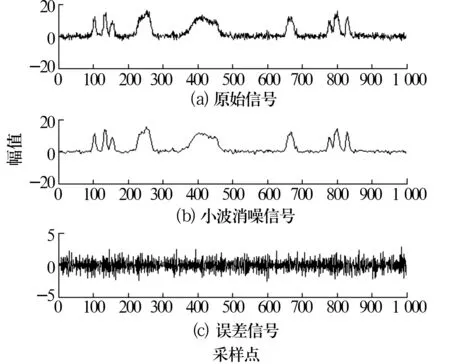
图1 noisbump信号的小波消噪结果

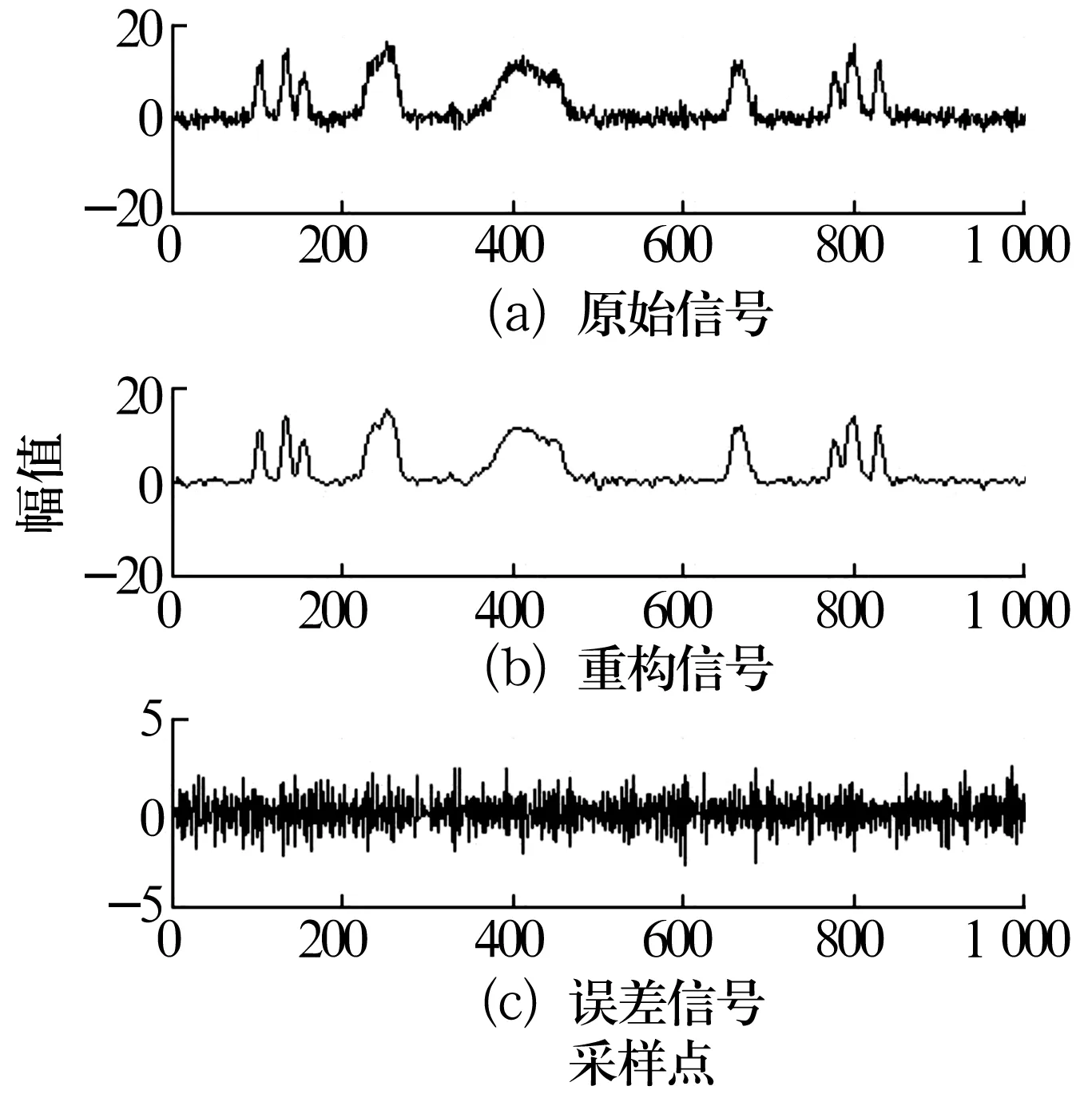
图2 noisbump信号的自适应冗余第2代小波消噪结果

3 应用示例

在某矿进行提升机振动测试时，根据对故障信号反应敏感及安装拆卸方便等原则，在提升机电动机、减速器及滚筒等关键部件两端轴承处分别安装两相或三相振动传感器。现场监测时，当发生故障时，信号中常常混入高频信息，所以采用频率范围较宽的压电式振动加速度传感器。提取型号为23296的双列向心调心滚子轴承的振动信号，信号采集时，轴承转速为250 r/min，其内圈故障特征频率理想值为fi=92 Hz[9]。

采集信号的时域波形如图3所示，由时域波形分析，该信号为非平稳信号，且伴随着峰值较高的振动序列。

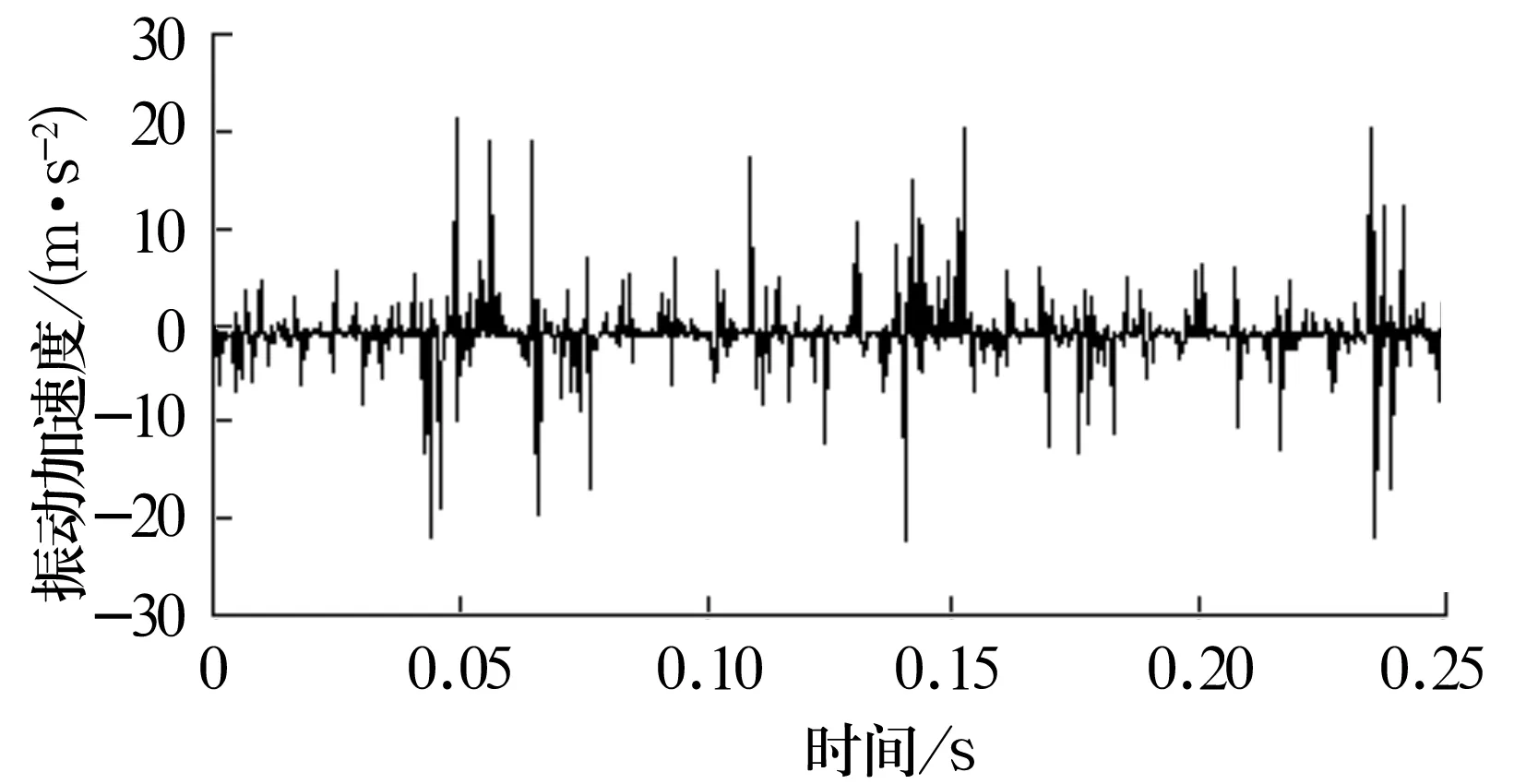
图3 轴承振动信号时域波形

利用MATLAB与LabVIEW混合编程实现自适应冗余第2代小波变换与HHT算法，并使用该方法对振动信号进行分析。首先使用自适应冗余第2代小波算法对信号进行消噪处理，得消噪后信号如图4所示。

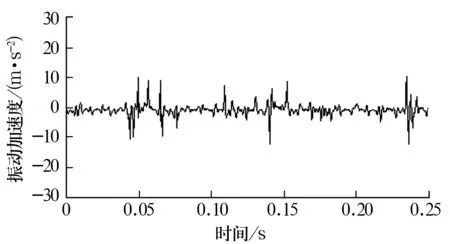
图4 振动信号的自适应冗余第2代小波消噪结果

比较可见，自适应第2代小波很大程度上降低了信号的噪声，使得信号的局部特征信息更加丰富。对消噪信号进行EMD分解，依次得到从高频到低频的7个IMF分量和1个剩余分量，分解结果如图5所示。不同IMF分量的时间尺度不同，将信号所含的不同频率分开，其中IMF1～IMF3是由传感器谐振和固有频率产生的高频成分，IMF4～IMF7是包含故障信息的低频段分量，r为剩余分量。

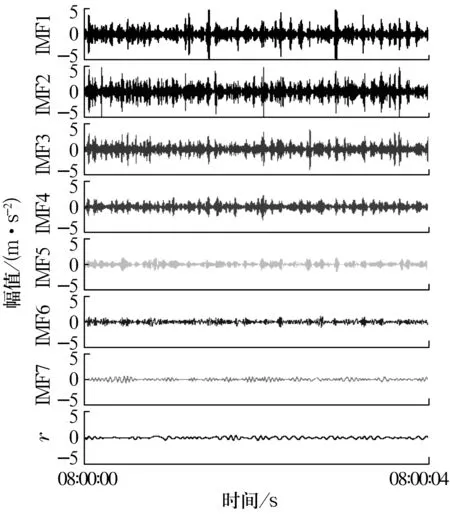
图5 振动信号的EMD分解

选取部分低频段分量进行Hilbert边际谱分析，得边际谱如图6所示。从图中可看出，在轴承内圈故障特征频率fi=92 Hz及其约3倍频270 Hz处存在明显的峰值谱线，而提取其他同型号轴承的振动信号进行分析，得边际谱如图7所示，从

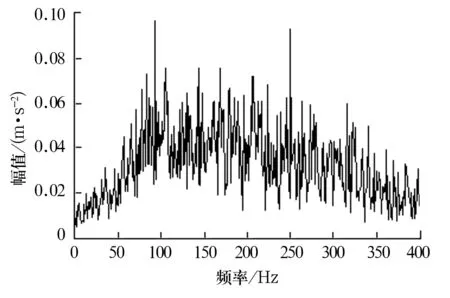
图6 故障轴承振动信号的Hilbert边际谱

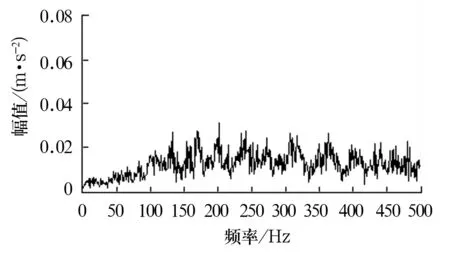
图7 正常轴承振动信号的Hilbert边际谱

图中可看出正常轴承振动信号频率分布较低，没有明显突起的频率点存在，故可断定此轴承内圈存在故障。

4 结束语

将第2代小波算法与HHT算法结合并应用到滚动轴承故障诊断中。构造自适应冗余第2代小波并借助其良好的消噪特性对振动信号进行消噪处理，对比分析了不同的消噪处理方法，验证了所用方法的优越性。对消噪后信号利用具有高频分辨率的自适应HHT算法提取信号故障特征。试验结果验证了第2代小波与HHT算法可有效滤去振动信号噪声并提取信号特征，且具有更高的频率分辨率，能够有效完成轴承的故障诊断。