基于Vague集相似度量的滚动轴承故障诊断

陈金梅，金誉辉，黄更平

(1.广西工业职业技术学院，南宁 530003；2.广西特种设备监督检验院，南宁 530219)

轴承是旋转机械中使用最多、最为关键且最易损坏的机械零件[1]。据统计，旋转机械的故障有30%是由轴承引起的，可见轴承的好坏对机器的工作状态影响很大，所以对滚动轴承的故障诊断和监测一直是近年来国内、外开展机械故障诊断技术的重点。滚动轴承故障诊断常用的方法是小波分析法和智能诊断技术。

小波分析法包括小波变换方法和小波包变换方法，其是最近几年才出现并得以应用和发展的一种时频信号分析方法。由于它具有时域和频域的局部化和可变时频窗的特点，分析非平稳信号的效果较好[2]。其缺点是计算过程比较复杂，计算工作量较大。

智能诊断技术就是把神经网络、专家系统及模糊理论等技术与滚动轴承的特征参数有机地结合起来进行综合分析的故障诊断技术。神经网络是对人脑神经组织结构和行为的模拟。故障诊断专家系统是一种典型的知识处理系统，它能获取大量的专家诊断知识，利用专家的推理方法，解决故障诊断领域的问题。模糊故障诊断方法是利用模糊集合论中的隶属函数的概念，解决故障与征兆关系的模糊不确定性与故障的早期预报及精密诊断的方法。由于模糊集的隶属函数是一个单一的值，它不能同时表示支持和反对的证据，为此，提出了Vague集概念。Vague集是模糊集的一种推广形式，常应用于模糊控制、决策分析及模式识别等领域，而相似度量是其中的关键技术[3]。

随着机械故障诊断技术的发展，单一的信号处理技术已经不能很好地满足故障诊断要求，各种信号处理技术相互融合成为发展方向。鉴于此种情况，采用小波包变换法处理得到的数据，再应用2种Vague集相似度量的方法对滚动轴承的故障进行研究，最后给出它们在模式识别中的应用示例。

1 基本理论

1.1 Vague集基本概念

定义1[4]：设X是一个点(对象)空间，其中任意一个元素用χ表示，X上一个Vague集V用一个真隶属函数tv和一个假隶属函数fv表示，tv(x)是从支持χ的证据导出的χ的肯定隶属度的下界，fv(x)是从反对χ的证据所导出的χ的否定隶属度的下界，tv(x)和fv(x)将区间[0,1]中的一个实数和X的每一点联系起来，即tv：X→[0,1]，fv：X→[0,1]，χ关于V的隶属度V(x)表示为：[tv(x),1-fv(x)]，其中，0≤tv(x)+fv(x)≤1。

设A和B是离散型论域X={x1,x2,…,xn}上的2个Vague集，其中

(1)

(2)

式中:VA(xi)=[tA(xi),1-fA(xi)],为Vague集A中χi的隶属度；VB(xi)=[tB(xi),1-fB(xi)],为Vague集B中χi的隶属度，i=1,2，…,n。

1.2 Vague集相似度量

定义2[5]：设X是一个非空集合，V是X上所有的Vague集组成的集合，A∈X，B∈X，S:V×V→[0,1],若S(A,B)满足条件：

(1)0≤S(A,B)≤1;

(2)S(A,B)=1当且仅当A=B；

(3)S(A,B)=S(B,A);

(4)S(A,B)=0当且仅当VA(xi)=x[0,0]，VB(xi)=x[1,1]或VA(xi)=x[1,1]，VB(xi)=x[0,0]；

(5)若A⊆B⊆C，则S(A,B)≤min(S(A,B),S(B,C))。则称S(A,B)为Vague集A和B的相似度量。

2 两种新的Vague集相似度量

2.1 Vague值之间的相似度量

设x=[tx,1-fx]，y=⎣ty,1-fy⎤ 是论域上的2个Vague值，它们之间的相似度量公式为[6]

(3)

对|tx-ty|和|fx-fy|赋予相同的权值0.5，并推广到一般的情形。

M1(x,y)=1-λ1max(|tx,ty|,|fx,fy|)-λ2min(|tx,ty|,|fx,fy|),

(4)

式中：λi(i=1,2)为加权因子，且满足0<λ1<1,0<λ2<1,λ1+λ2=1,λ1≥λ2。λ1,λ2的取值只要满足上述条件即可，并不影响结果的判断[7]。

对(3)式进行归一化处理，得到另一相似度量的公式：

(5)

M1(x,y)和M2(x,y)都是满足定义2中5个条件的Vague值相似度量。

2.2 Vague集之间的相似度量

Vague集A,B如(1)，(2)式所示，其Vague集之间的相似度量为：

(6)

(7)

S1(A,B)和S2(A,B)都是满足定义2中5个条件的Vague值之间的相似度量。其值都在[0,1]区间；相似度量值越小，代表两者差异越大；相反，相似度量值越大，代表两者越相似。

3 算例

采集7001AC滚动轴承样本数据和待测数据共5组:其中第1组正常，第2组为内圈故障，第3组为外圈故障，第4，5组为待测样本(分别为正常、内圈故障)[8]，经过小波包分解得到8维特征向量，归一化处理结果见表1。

表1 以Vague值表示滚动轴承的样本数据和待测数据

根据前文Vague集(值)相似度量的理论，滚动轴承5组数据构成论域X={x1,x2,…,x8}，则X上8维特征向量用Vague集表示(其中，A1正常；A2内圈故障；A3外圈故障;B1，B2为待检测样本)：

A1=[0.511 2,0.556 3]/x1+[0.054 2,0.074 2]/x2+[0.068 0,0.071 9]/x3+[0.062 5,0.071 9]/x4+[0.068 5,0.073 7]/x5+[0.066 7,0.071 8]/x6+[0.059 2,0.063 7]/x7+[0.052 2,0.056 8]/x8；

A2=[0.148 5,0.159 7]/x1+[0.117 3,0.129 2]/x2+[0.150 4,0.202 2]/x3+[0.118 5,0.146 5]/x4+[0.065 1,0.084 9]/x5+[0.086 2,0.106 3]/x6+[0.136 5,0.137 2]/x7+[0.097 7,0.114 1]/x8；

A3=[0.147 9,0.153 6]/x1+[0.099 0,0.102 9]/x2+[0.149 4,0.171 6]/x3+[0.138 0,0.153 9]/x4+[0.118 5,0.137 5]/x5+[0.082 7,0.105 4]/x6+[0.118 1,0.132 4]/x7+[0.090 2,0.099 0]/x8；

B1=[0.536 9，0.545 2]/x1+[0.043 5,0.054 0]/x2+[0.054 3,0.061 0]/x3+[0.050 0,0.062 3]/x4+[0.055 3,0.066 0]/x5+[0.056 1,0.065 9]/x6+[0.050 2,0.062 8]/x7+[0.045 3,0.052 1]/x8；

B2=[0.142 4,0.152 8]/x1+[0.102 1,0.120 0]/x2+[0.177 9,0.185 0]/x3+[0.129 4,0.138 0]/x4+[0.069 8,0.074 4]/x5+[0.091 2,0.100 3]/x6+[0.129 0,0.141 2]/x7+[0.101 2,0.109 4]/x8。

然后，用(4)式、(5)式计算样本数据和待测数据Vague值之间的相似度量。计算过程分别取λ1=0.75，λ2=0.25，计算结果见表2。

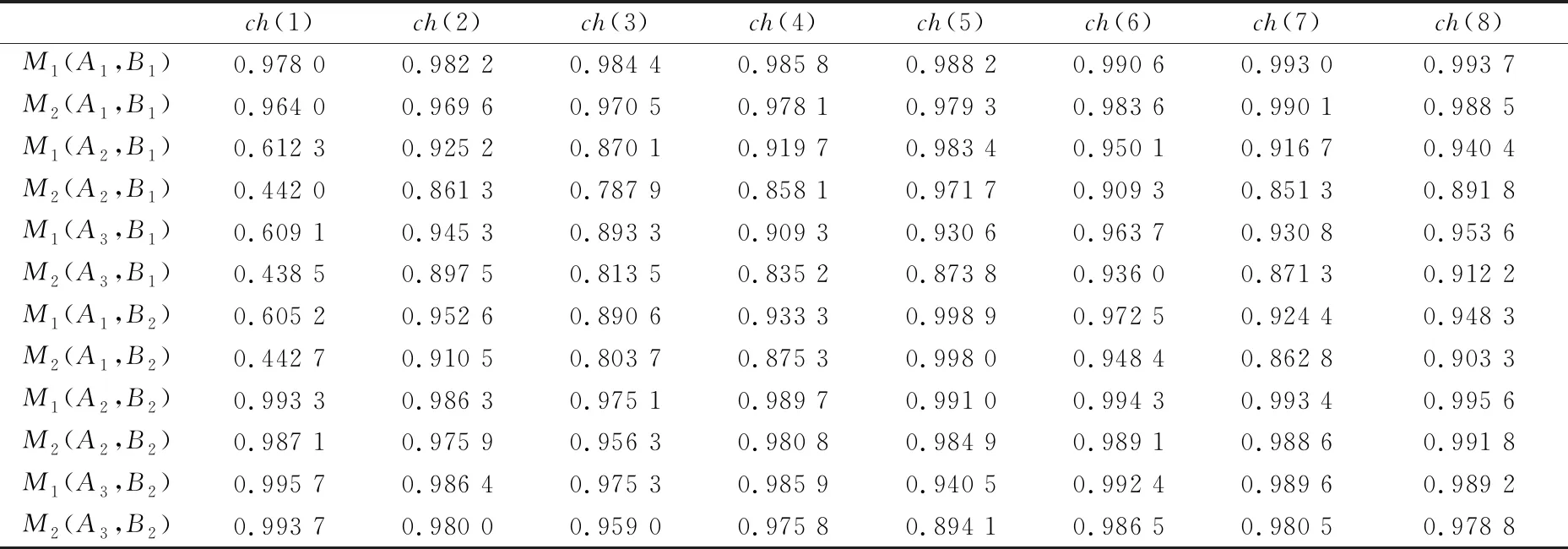
表2 待测数据与样本数据Vague值之间的相似度量

最后，用(6)式、(7)式计算样本数据和待测数据Vague集之间的相似度量，计算结果见表3。

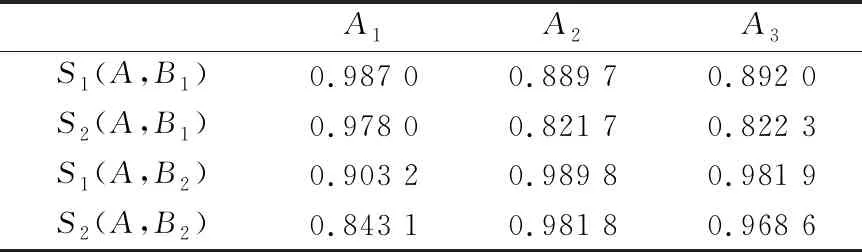
表3 待测数据与样本数据Vague集之间的相似度

由于相似度量是反映待检测样本接近故障类型的度量，若某一相似度量值越大，则待测样本就越接近某一类故障类型。

从表3可知，第4组待测样本诊断结果的大小顺序为：S1(A1，B1)>S1(A3,B1)>S1(A2,B1)，S2(A1,B1)>S2(A3,B1)>S2(A2，B1)。两种Vague集相似度量方法的结果一致。首先是正常，与文献[8]模糊聚类方法结果相同，其次是外圈故障，最后是内圈故障。

第5组待测样本诊断结果的大小顺序为：S1(A2，B2)>S1(A3，B2)>S1(A1,B2),S2(A2,B2)>S2(A3，B2)>S2(A1，B2)。两种Vague集相似度量方法的结果一致。首先是内圈故障，与文献[8]模糊聚类方法结果相同，其次是外圈故障，最后是正常。

从故障的结果看，该方法比模糊聚类方法要简单，3组数据即可对待测样本进行判断，模糊聚类方法则很难实现；同时给出了发生多个故障的顺序，这也为故障诊断提供了理论依据。

4 结束语

从示例分析可以看出，基于Vague集相似度量的故障诊断方法与模糊聚类方法和试验结果一致，证明了该方法的合理性。除此之外，该方法还可以应用到汽轮机、通风机及变压器等设备的故障诊断中。