新型智能轴承的结构与监测能力分析

2012-07-20邵毅敏涂文兵叶军

轴承 2012年5期

邵毅敏，涂文兵，叶军

(1．重庆大学机械传动国家重点实验室，重庆 400030；2．洛阳轴研科技股份有限公司，河南洛阳 471039)

智能轴承是在传统轴承基础上集成不同用途的传感器，使其结合成为一体而形成的独特结构单元。由于传感器接近故障发生源，不仅可大幅提高信噪比以及早期故障诊断的成功率，而且还可对设备运行的参数进行实时监测，实现设备运行状态的综合分析，是设备状态监测与故障诊断的一个重要发展方向。

智能轴承一般由轴承本体、微型复合传感器、信号传输电路、信号的处理与分析系统4大部分组成。轴承本体与复合传感器的结合，一般要在轴承本体上开槽。不合理的沟槽会影响轴承本体的应力分布，导致过早失效，从而使智能轴承丧失功能。为保证智能轴承的可靠性，有必要分析沟槽参数对轴承变形和应力分布的影响，为智能轴承结构的设计提供理论依据。

文献[1-2]采用有限元法研究了嵌入式智能轴承外圈改造对轴承承载能力的影响。文献[3-4]采用有限元法研究槽结构参数对嵌入式智能轴承外圈最大应力和最大变形的影响。文献[5]采用ANSYS对嵌入式智能轴承进行有限元分析，研究槽的尺寸对轴承最大变形和最大应力的影响。目前智能轴承结构的参数分析，主要采用有限元法分析外圈沿轴向的凹槽对轴承应力和变形的影响，对外圈沿圆周方向的凹槽的研究较少。

下文重点分析了复合传感器与轴承本体结合部的结构参数对轴承本体变形和应力分布的影响；研究了模拟和物理试验台架条件下智能轴承的监测能力，并与传统监测方法进行了对比分析。

1 新型智能轴承结构

新型智能轴承结构如图1所示，在传统轴承端面安装有复合传感器(图2)，复合传感器由2个形状相同的上半圆壳体和下半圆壳体对接构成中央有通孔的圆盘壳体，该圆盘壳体的内圈和外圈均按同一方向轴向弯折延伸形成凸台，在两凸台之间的壳体上装有电路板，在圆盘壳体内圈的凸台上嵌接有加速度传感装置、速度传感装置和温度传感装置，在圆盘壳体外圈的周面上还装有另一个温度传感装置，各传感装置的输出线分别与所述电路板上的放大器输入端相连，经各放大器处理后，再将信号输出。新型智能轴承将振动传感装置和温度传感装置、速度传感装置集成一体，能有效提取轴承和机械设备的状态信号[6]。

图1 智能轴承结构示意图

图2 复合传感器结构示意图

新型智能轴承可应用于深沟球轴承、圆柱滚子轴承和圆锥滚子轴承等多种类型的轴承，外形与普通轴承类似，安装方法也与普通轴承一样，具有较广阔的应用前景。

2 外圈凹槽的应力-应变分析

新型智能轴承以双列圆柱滚子轴承为例，相关参数见表1。在此采用有限元分析方法分析复合传感器与轴承本体结合部的结构(即外圈凹槽的结构参数)对轴承本体变形和应力分布的影响。

表1 双列圆柱滚子轴承参数

2.1 有限元模型的建立

为控制有限元模型规模，同时保证计算精度，有限元模型采用8节点六面体单元进行离散，并对接触位置进行局部细化。为提高分析效率，截取智能轴承的一段进行结构分析，精度与整体模型基本一致[2, 4]，由于外圈的应力和变形是由滚子的接触载荷产生，建立滚子1/2模型以便于加载。

智能轴承结构分析有限元模型如图3所示，在ANSYS中，选择单元类型为solid185，并建立滚子与外圈以及外圈与复合传感器壳体之间的接触关系。轴承所使用的材料一般为高强度轴承钢，材料模型选择弹性材料，弹性模量为210 GPa，泊松比为0.3，密度为7 830 kg/m3。

图3 智能轴承结构分析有限元模型

2.2 载荷及其边界条件

轴承的径向载荷为Fr=50 kN，根据轴承内部载荷分布[7]，双列滚子轴承中最大滚子载荷为Q=4.6Fr/(2Z)，经计算Q=3 710 N，将载荷Q施加在有限元模型上，约束滚子转动自由度并对外圈和复合传感器壳体外表面施加位移约束。

2.3 结构参数对轴承变形和应力分布的影响

如图4所示，复合传感器与轴承本体的结合方式一般采用凸缘与凹槽结构。其中，轴承凹槽的结构参数包括外圈凹槽深度h1、凹槽宽度L1和凹槽距轴承本体外圈端面距离L2；复合传感器壳体的结构参数有复合传感器壳体厚度h2和复合传感器壳体宽度L3。

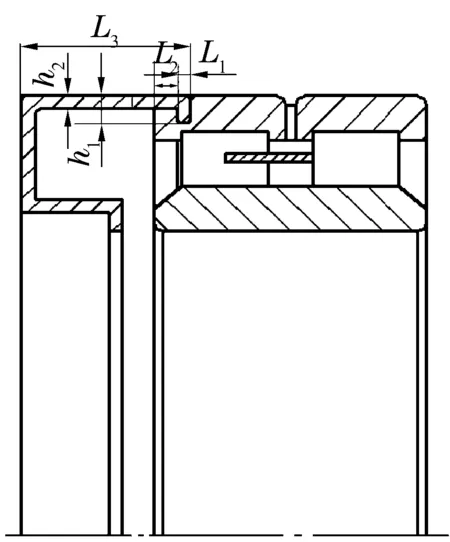
图4 复合传感器与轴承本体的结合

计算分析的结构参数为：h1=2 mm，L1=3 mm，L2=5 mm，h2=3 mm，L3=37 mm，复合传感器壳体材料选择45#钢。

智能轴承的应力和变形云图分别如图5和图6所示，应力和变形主要集中在滚子与外圈的接触部位，最大应力286 MPa位于接触部位的无槽一侧，最大变形0.002 25 mm位于接触部位的有槽一侧。智能轴承的最大应力远小于轴承钢的屈服强度(约1 700 MPa)，最大变形也处于较低水平，表明凹槽结构对轴承本体的影响很小。

图5 轴承的应力云图

图6 轴承的变形云图

智能轴承最大应力和最大变形随凹槽深度的变化曲线如图7所示。最大变形随槽深的增加呈指数形式增加，槽深的增加存在极限值h1Lim(外圈厚度的85%左右)，槽深超过极限值后最大应力会急剧增加。

图7 最大应力和最大变形随凹槽深度的变化曲线

智能轴承最大应力和最大变形随凹槽宽度的变化曲线如图8所示，最大应力和最大变形随槽宽增大基本呈线性增加。智能轴承最大应力和最大变形随凹槽距轴承本体端面距离的变化曲线如图9所示，凹槽越靠近轴承本体端面，最大变形和最大应力越小，当凹槽与外圈端面的距离超过L2Lim(5 mm)时，最大应力和最大变形变化速率增大。

图8 最大应力和最大变形随凹槽宽度的变化曲线

图9 最大应力和最大变形随凹槽位置的变化曲线

3 智能轴承监测能力的分析

3.1 轴承内圈故障的有限元模型

轴承内圈故障的有限元模型如图10和图11所示。其中，x为轴承轴向方向，y为轴承竖直方向，z为轴承水平方向。模型采用8节点六面体单元进行映射网格划分；基于罚函数法建立轴承滚子与内、外圈及保持架之间的接触关系；采用共节点方式处理外圈与轴承座间的过盈配合关系，采用显式动力学分析软件LS-DYNA进行轴承运转过程的动态仿真。内圈故障位置如图12所示。仿真条件为：径向载荷1 380 N，内圈转速分别为390 ，480，660，750 和930 r/min。

图10 智能轴承-轴承座有限元模型

图11 智能轴承有限元模型

图12 故障内圈的有限元模型

3.2 监测能力的对比分析

传统故障监测诊断方法一般是将传感器安放在轴承座上，智能轴承的传感器则更靠近故障源。为了对比两种方法的故障监测能力，在径向载荷1 380 N、转速390 r/min工况条件下进行了模拟仿真。智能轴承和轴承座上的竖直方向0.2～0.6 s内的振动加速度信号如图13和图14所示。智能轴承上的加速度信号峰值为30g(g为重力加速度，g=9.8 m/s2)，轴承座上的加速度信号峰值为5.7g。轴承座上的振动加速度幅值远小于智能轴承上的振动加速度幅值。

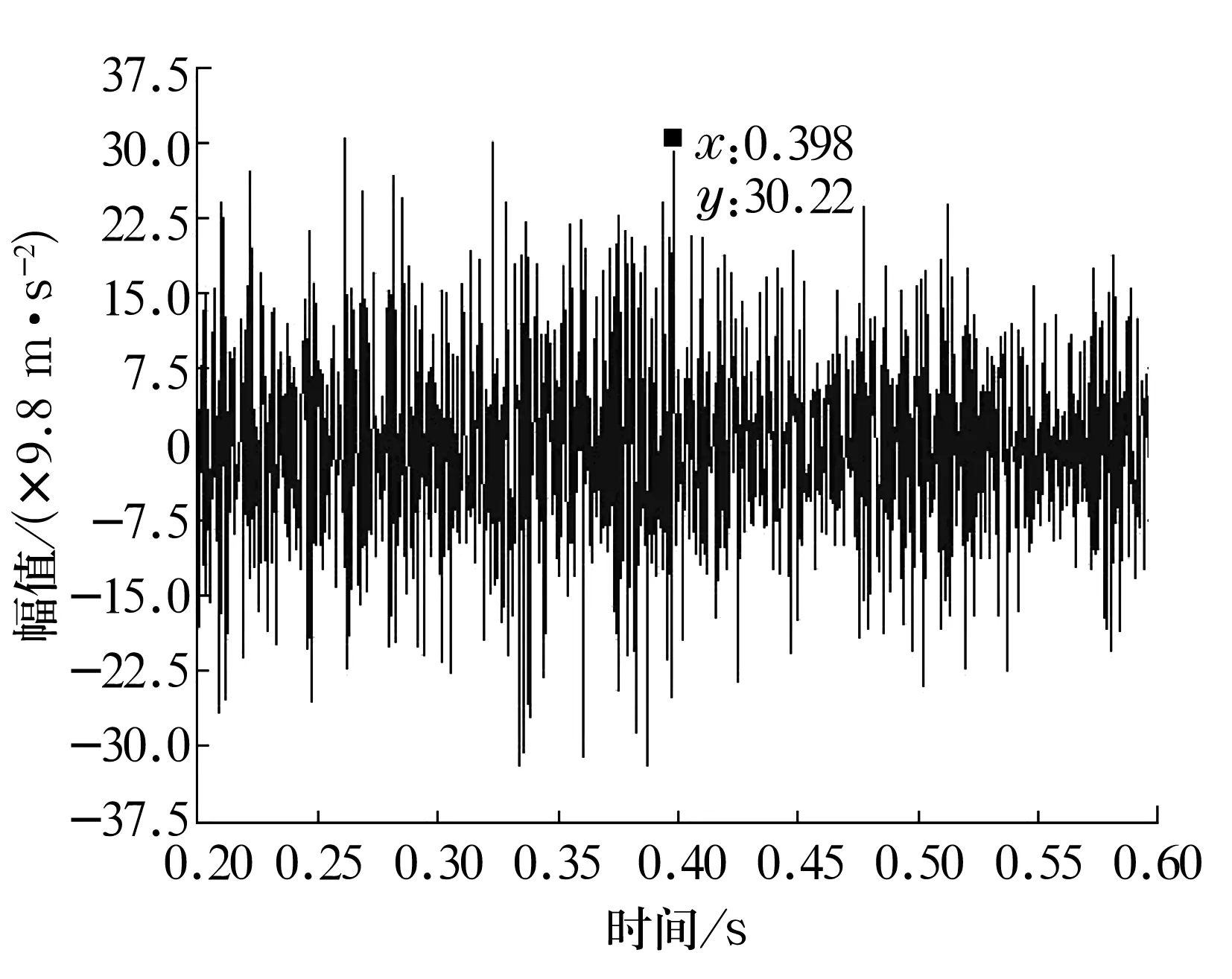
图13 智能轴承加速度信号的时域波形

图14 轴承座加速度信号的时域波形

智能轴承与轴承座上的竖直方向加速度信号的均方根值(RMS值)和峰值随转速变化曲线如图15所示。RMS值随转速呈线性增加趋势，峰值随转速增加亦呈增大趋势，但转速增加到一定值后峰值变化趋于平缓。

图15显示轴承座上获取加速度信号的RMS值和峰值均远小于智能轴承上获取的加速度信号的RMS值和峰值，表明智能轴承上的振动能量和冲击能量远大于轴承座。

图15 轴承座与智能轴承的时域统计参数对比

上述结果表明，智能轴承对故障激励非常敏感，能很好地捕捉缺陷信息，克服了传统故障监测方法因故障冲击信号受传递路径衰减和被噪声淹没，难于准确提取的缺点。

3.3 台架试验验证与对比分析

智能轴承试验台如图16所示，其可模拟轴承的运转过程且转速可调，同时可实现径向和轴向加载。智能轴承和传统方法采集到的信号经过预处理及A/D转换后进入状态监测和分析软件，进行数据的显示和分析处理。试验过程中智能轴承径向加载1 380 N，转速分别为390，480，660，750和930 r/min。以内圈故障为例，并作为故障激励源来比较传统诊断方法和智能轴承检测方法在监测能力上的差别。

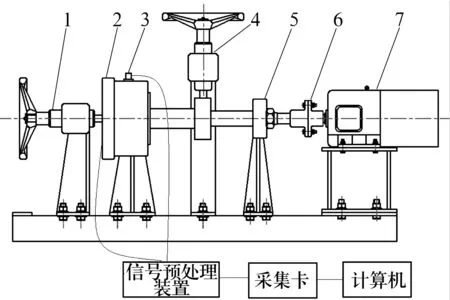
1—轴向加载装置；2—大轴承座；3—振动传感器；4—径向加载装置；5—小轴承座；6—联轴节；7—驱动电动机

计算不同转速条件下，智能轴承获取的加速度信号和传统方法获取的加速度信号的RMS值与峰值，仿真结果与台架试验结果如图17所示。传统方法的值集中在低值区域，智能轴承的值处于高值区域，智能轴承的感知能力明显高于传统方法的感知能力，即在相同故障激励及不同转速情况下，智能轴承均比传统方法具有更高的信号感知能力。