角接触球轴承凸出量的灰色关联度分析

张艳丽，王平，李志刚，杨友中，邹燕珍

(1.洛阳LYC轴承有限公司，河南 洛阳 471039；2.洛阳轴研科技股份有限公司，河南 洛阳 471039)

成对或多联组配角接触球轴承除了满足单套轴承的常规技术要求外，还必须确保轴承内径尺寸相互差、外径尺寸相互差、内圈和外圈的径向跳动相互差、接触角、预载荷、游隙和凸出量等满足技术要求。除凸出量外的上述指标在实际加工中均是可测和可控的，可以通过直接控制工艺参数来满足产品的配对要求。

凸出量是轴承装配的一个重要技术指标，并且受众多因素综合影响。本例所述的分析方法是从众多影响因素中寻找并确定其主要因素，采取相应措施，为凸出量选配奠定基础。凸出量是指：对单个轴承施加预载荷后，轴承同一端面处，一套圈端面相对于另一套圈端面凸出的距离。凸出时，用“+”表示；凹进时，用 “-”表示。组配轴承配对是否成功，关键就在于两套或多套组配轴承在某一轴向载荷作用下凸出量是否相匹配，因为只有凸出量相配合的两套或多套轴承才能获得相同的预紧力，从而确保配对轴承正常工作。所以从一定角度上说轴承组配实际上就是选配适宜的凸出量。

影响凸出量的因素较多，其中内、外圈宽度，内、外圈沟道位置、沟曲率半径以及游隙等与凸出量之间的关系可以看成是灰的，属于乏信息系统的范畴[1]。分不清哪些因素关系密切，哪些不密切，就很难找到主要矛盾，发现主要特征及主要关系。所以灰色因素间的关联度分析[2]实际上是灰色系统分析、预测及决策的基石。在凸出量与影响因素的模型中，用关联度来表征主要因素对凸出量的影响。

1 基本思路

灰色关联度分析，从思路来看，属几何处理的范畴。主要是根据测量数据序列之间的距离与几何形状的相似性，来评价各数据序列之间的关联性[1]。例如，图1有3个用曲线描述的数据序列，以曲线X1(t)为主要研究对象，从直观上可以看出，曲线X1(t)和X2(t)的形状比较相似，二者的关联度γ12就比较大；曲线X1(t)和X3(t)的形状有比较大的差异，二者的关联度γ13就比较小。若按照关联度从大到小排序，则有γ12>γ13。相应的序列{γ12,γ13}称为灰关联度序，表示相对X3(t)来说，X2(t)与X1(t)的之间的关系更密切。

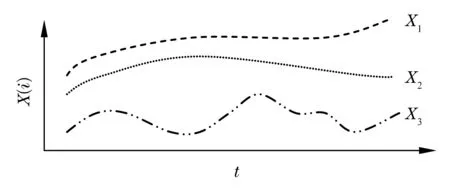
图1 曲线的相似性

2 灰色关联度分析方法

2.1 灰色关联度系数

设母素数序列Xi为

Xi={Xi(1),Xi(2),Xi(3)，…，Xi(k)，…，Xi(n)}，i=1,2,…,n，k=1,2,…,n。

子因素Xj为

Xj={Xj(1),Xj(2),Xj(3)，…，Xj(k)，…，

Xj(n)}，j=1,2,…,n，k=1,2,…,n。

定义绝对值差

Δij=|Xi(k)-Xj(k)|。

(1)

最小绝对值差

最大绝对值差

(2)

Xi与Xj在k时的关联系数为

(3)

式中：K为分辨率系数，K∈(0,1)。

2.2 关联度γ

(4)

式中：γij为xj对xi的关联度。

2.3 数据预处理——初值象(模糊理论)

无量纲初值“1”

设原始序列x0={x0(1),x0(2),…,x0(k),…,x0(n)} ，

预处理后

x={x(1),x(2),…,x(k),…,x(n)} ，

(5)

x为初值象，实际计算时，就有Δmin=0，这时有0.5≤ξij≤1。

3 应用实例

采集了7016ACTB/P4DBB 轴承的4组内、外圈的宽度(B，C)、沟位置(ai,ae)、沟曲率半径(ri,re)、沟道直径(F,E)、配套游隙(Gr)和同一载荷下轴承凸出量等数据。按加工顺序记录数据，比较各因素与凸出量的关联情况，详细数据见表1 。

表1 原始检测数据 mm

注：“-”表示内圈非基准端面高出外圈基准端面。

则，x0=(-0.102，-0.099，-0.106，-0.107)，

x1=(-0.009 5，-0.022 5，-0.016，-0.061 5)，

x2=(11.298 5，11.275 5，11.268，11.280 5)，

x3=(6.636， 6.666， 6.647， 6.639)，

x4=(-0.018，-0.002，-0.006，-0.004)，

x5=(-0.026，-0.016 5，-0.029，-0.026 5)，

x6=(11.012，11.014 9，11.022，11.029)，

x7=(7.008，7.001，6.998，7.004)，

x8=(-0.008，-0.002，-0.006，-0.045)，

x9=(0.168， 0.178， 0.168， 0.174)。

以凸出量为母素数序列分别比较内、外圈各因素的关联情况。

由(5)式初值归一化得

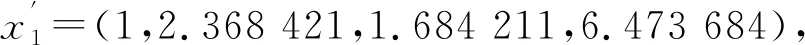
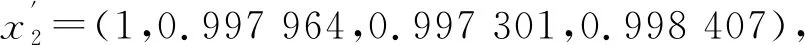
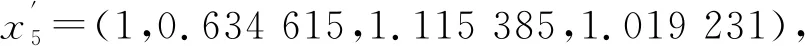
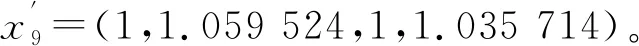
初值化数据见表2。由(1)式求绝对值差。在Δ01中，k=2,j=2 时，

表2 初值化数据

k=3,j=3时，

k=4,j=4 时，

所以有Δ01=(0，1.397 833，0.644 995，5.424 664)。

同理

Δ02=(0，0.027 378，0.041 915，0.050 613)，

Δ03=(0，0.033 933，0.037 558，0.048 568)，

Δ04=(0，0.085 947，0.070 588，0.826 797)，

Δ05=(0，0.335 973，0.076 169，0.029 789)，

Δ06=(0，0.029 675，0.038 308，0.047 476)，

Δ07=(0，0.028 413，0.040 643，0.049 590)，

Δ08=(0，0.720 588，0.289 216，4.575 980)，

Δ09=(0，0.889 360，0.039 216，0.013 305)，

Δmin=0，

Δmax=5.424 664。

当K=0.5时，由(3)式确定关联系数。

在ξ01中，k=1时，

k=2时，

0.659 908;

k=3时，

0.807 884;

k=4时，

0.333 333。

所以有ξ01=(1，0.659 908，0.807 884，0.333 333)。

同理，有

ξ02=(1，0.990 008，0.984 782，0.981 682)，

ξ03=(1，0.987 644，0.986 342，0.982 409)，

ξ04=(1，0.759 372，0.793 494，0.766 384)，

ξ05=(1，0.659 908，0.807 884，0.989 137)，

ξ06=(1，0.989 179，0.986 073，0.982 797)，

ξ07=(1，0.989 633，0.985 237，0.982 045)，

ξ08=(1，0.790 095，0.903 644，0.372 148)，

ξ09=(1，0.968 252，0.985 748，0.995 118)。

按(4)式确定灰色关联度，由于数据较多，故采用平均值进行计算。

0.700 282，

0.989 118,

同理，γ03=0.989 099,γ04=0.829 812,γ05=0.864 232,γ06=0.989 512,γ07=0.989 229,γ08=0.766 472,γ09=0.987 279。

外圈的关联度为

γ02(外圈沟位置)>γ03(外圈沟曲率半径)>γ04(外圈沟道直径)>γ01(外圈宽度)。

内圈的关联度为

γ06(内圈沟位置)>γ07(内圈沟曲率半径)>γ05(内圈宽度)>γ08(内圈沟道直径)。

内、外圈的关联度为

γ06(内圈沟位置) >γ07(内圈沟曲率半径)>γ02(外圈沟位置)>γ03(外圈沟曲率半径)>γ09(游隙)>γ05(内圈宽度)>γ04(外圈沟道直径)>γ08(内圈沟道直径)>γ01(外圈宽度)。

4 结束语

由以上分析可知：影响凸出量的重要因素依次是内、外圈沟位置，内、外圈沟曲率半径及游隙。为了将沟位置控制在一定范围内，须严格控制套圈的宽度，为此建议采用双端面磨削套圈，精研时采用套研工艺，力争使内、外圈等高；磨削内、外沟道时最好采用高精度沟道磨床以及高精度测量仪器，尽量保证沟位置的一致性，控制沟曲率半径的相互差，使轴承合套径向游隙控制在要求的范围内，为凸出量选配奠定基础。