输电线路两相短路故障行波分析

袁 圆 哈恒旭 王奎鑫 秦 浩

1.山东理工大学电气与电子工程学院 山东 淄博 255049；

2.安徽省电力公司淮南供电公司 安徽 淮南 232000

0 引言

电力系统中，为了能快速有效地对故障进行修复，及时恢复系统供电，对线路故障点进行准确定位显得十分重要。行波理论应用于输电线路故障测距国内外己做了大量研究[1-4]。故障行波分析是行波故障定位的基础，对于输电线路单相接地故障的行波分析已经有很多研究[1，5]，但对于两相短路的研究相对而言较少。本文采用凯伦贝尔矩阵进行相模变换，对三相互相耦合的系统进行解耦，将其分解为互相独立的3个模量系统进行分析。分析了输电线路两相短路时，故障行波初始的产生过程，研究了线路发生两相短路故障时产生的暂态行波特征及与波阻抗、过渡电阻的关系，以及故障点的折、发射行波的幅值、极性的规律。

1 两相短路故障点的初始行波分析

当输电线路发生两相短路时，根据叠加原理，故障后的网络可以等效为故障前的正常运行的网络和故障附加网络的叠加[1]。例如当输电线路在某点发生BC两相短路故障时，就可等效为正常运行状态和故障附加状态，如图1所示。

（a）故障等效网络、（b）正常运行网络、（c）故障附加网络

图1 故障网络分解图

故障分量相当于系统电势为零时，在故障点处的B、C相之间叠加一个与该点正常状态下大小相等，方向相反的电压。在这一电压的作用下，产生由故障点F向线路两端传播的行波。图中Ucb为系统故障点故障前C相对B相的电压，暂态行波即为电源uf产生的。

由于故障后行波是由行波源uf产生的，所以我们只针对故障分量网络进行研究。由于三相系统存在着耦合，我们采用凯伦贝尔变换[2]进行解耦计算，变换矩阵及逆变换矩阵如下：

经过相模变换之后，而各个模分量是独立的，因而有：

式中：u0，u，uβ分为故障点的各模分量的电压行波，i0，i，iβ分别为故障点的各模分量的电流行波。z0，z1为输电线路零模波阻抗和线模波阻抗。即：

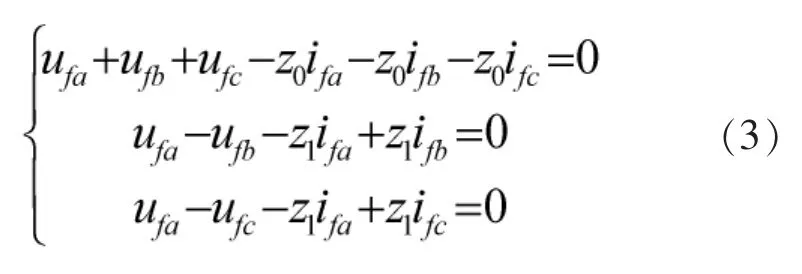
式中：ufa，ufb，ufc分别为故障点的三相行波电压;ifa，ifb，ifc分别为故障支路上的三相行波电流。

系统两相短路时有如下边界条件：

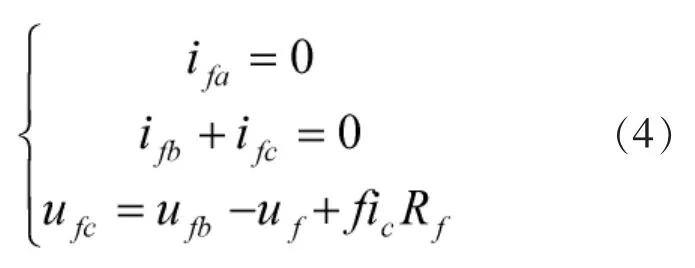
联立方程（1）、（3）、（4）、解方程可得到故障点的各相电压初始行波：

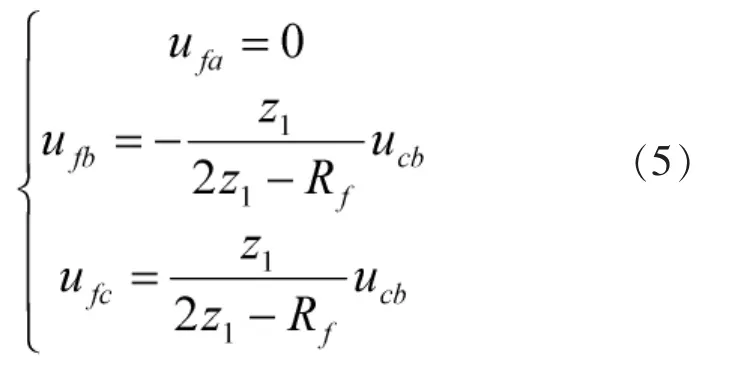
通过凯伦贝尔解耦变换之后，可得到各模量的电压初始行波：

进而由各模分量的相互关系可得到，线路个模量的电流初始行波：

由式（6）和式（7）可看出：两相短路故障情况下，电压、电流行波零模分量为零，即两相短路时不会出现零模电压行波和零模电流行波；电压及电流的两个线模初始行波大小相等、极性相反，其幅值随过渡电阻增大而减小，在发生两相金属性短路时初始行波最大。

2 两相短路故障点的折射行波分析

由于母线处、以及除故障点外的输电线路三相系统仍然是对称的[5]，而电压、电流的三个模分量独立，所以初始行波经母线反射之后到达故障点之前，三个模分量的相对关系也不变。由于故障点破坏了三相线路的对称性，当初始行波经母线反射之后到达故障点的时候，势必会有电场能和磁场能的重新分配[6-8]，即行波会发生折、反射现象。本节主要讨论行波的折射现象。由彼得逊法则，如图2所示，对每一模量的行波有如下关系：

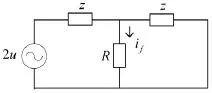
图2 单回路彼得逊法则

式中：u0、ua、uβ分别为入射电压波的零模和2个线模分量，u0f、uαf、uβf分别为故障点的折射电压波的各模分量。i0f、iαf、iβf分别为折射入故障之路的电流波的各模分量。

对故障点的每相分量还应满足如下的边界条件：

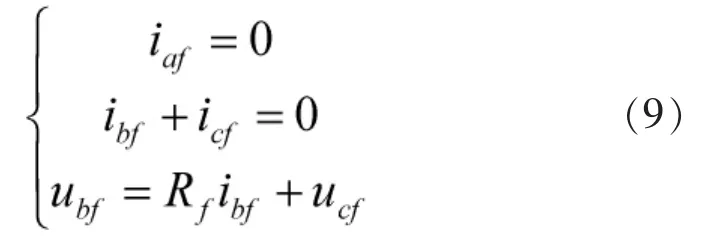
式中：iaf、ibf、icf分别为折射入故障之路的各相电流行波分量，ubf、ucf为故障点处B、C相的电压行波，Rf为故障过渡电阻。

通过凯伦贝尔变换将（9）式变换为各模分量：

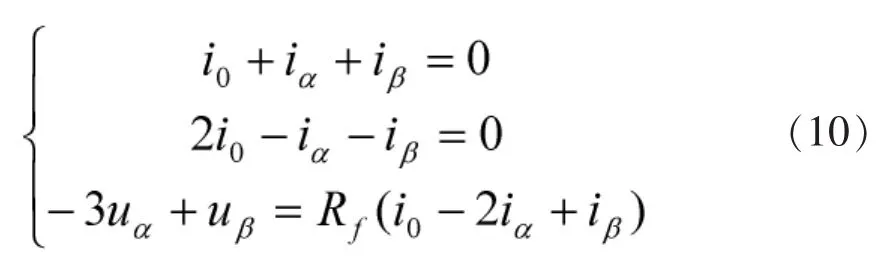
联立线性方程组（8）和（10），可求得个模量的折射电压波：

由上节分析知道，两相短路故障情况下，电压零模分量为零，电压及电流的两个线模初始行波大小相等、极性相反。可将式（11）简化为：

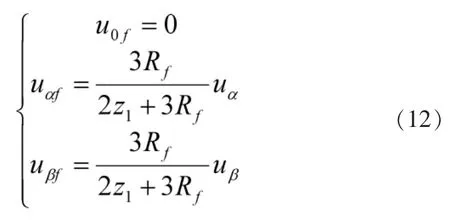
由式（12）各模电压分量，可得到各个模分量的折射电流波如下：

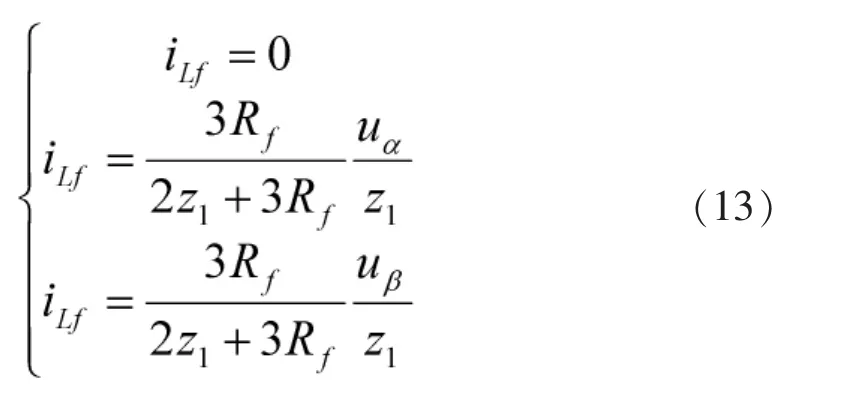
由式（12）、（13）可以知道，两相短路时，故障初始行波经母线反射后达到故障点时，电压行波与电流行波线模分量的折射系数相同，为，折射波与入射波的极性相同。折射波两个线模分量的极性相反，无零模分量。发生两相金属性短路时，折射系数为0，即发生全反射。

3 两相短路故障点的反射行波分析

由于故障点的电压只能有一个数值，所以故障点的折射电压波应该等于入射电压波与反射电压波的和[2]，根据这个关系，由式（12）可以由求出反射电压波：

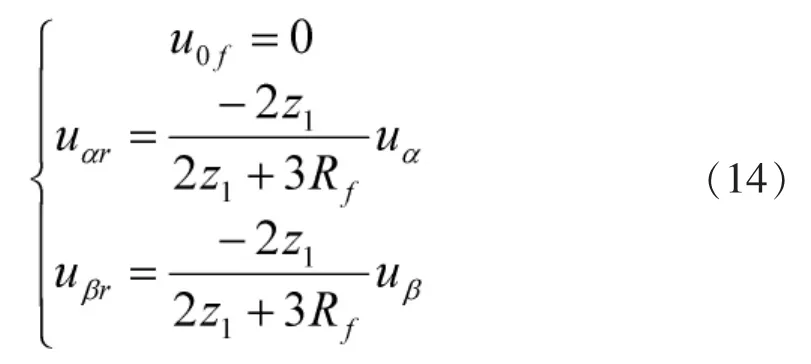
将式（14）代入行波的模量方程可得到电流的各模量行波：

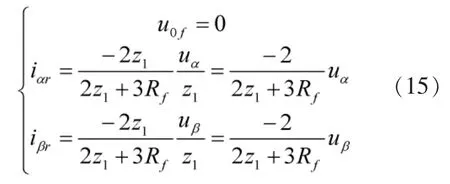
由式（14）、（15）可以知道，两相短路时，故障初始行波经母线反射后达到故障点时，电压行波与电流行波线模分量的反射系数相同，为，反射波与入射波的极性相反。反射波两个线模分量的极性相反，无零模分量。发生两相金属性短路时，反射系数为-1，即发生全反射。

4 结论

本文详细的分析了输电线路两相短路时，故障初始行波，故障点折、反射行波的大小、极性及与波阻抗、过渡电阻的关系，在理论分析的基础上得到了如下结论：

对于故障初始行波，两相短路故障时，电压、电流初始行波零模分量为零，即两相短路时不会出现零模电压行波和零模电流行波；电压及电流的两个线模初始行波大小相等、极性相反，其幅值随过渡电阻增大而减小，在发生两相金属性短路时初始行波最大。

对于故障点的折射波，两相短路故障时，故障初始行波经母线反射后达到故障点时，电压行波与电流行波线模分量的折射系数相同，随过渡电阻的增大，折射系数增大。折射波与入射波的极性相同，折射波两个线模分量的极性相反，无零模分量。发生两相金属性短路时，折射系数为0，即无折射波。

对于故障点的反射波，两相短路时，故障初始行波经母线反射后达到故障点时，电压行波与电流行波线模分量的反射系数相同，随过渡电阻的增大，反射系数减小，反射波与入射波的极性相反。反射波两个线模分量的极性相反，无零模分量。发生两相金属性短路时，反射系数为-1，即发生全反射。

[1] 施慎行，董新周，周双喜.单相接地故障行波分析[J].电力系统自动化，2005，29（23）：29-32.

[2] 葛耀中.新型继电保护和故障测距的原理与技术（M）.西安：西安交通大学出版社，2007.

[3] GREENWOODA.Electrical Transients in Power Systems.New York：John Wiiey&Sons Inc.1991.

[4] 董新洲，葛耀中，贺家李，郭效军，薄志谦.输电线路行波保护的现状与展望[J].电力系统自动化，2000，24 （10）：56-61.

[5] 季涛.中性点非有效接地系统故障行波暂态特征分析[J]，潍坊学院报，2007，7（6）：1-5.

[6] 施慎行，董新周.基于单相电流行波的故障选线原理研究[J].电力系统保护与控制.2008，36（14）：13-16.

[7] 马丹丹，王晓茹.基于小波模极大值的单端行波故障测距[J].电力系统保护与控制，2009，37（3）：55-59.

[8] 李杨，黄映，成乐祥.考虑故障时刻与波速选取相配合的行波测距.电力自动化设备，2010，30（11）：44-47.