解题教学中丰富学生的思维品质

王鹤新 胡生青

（1.江阴市第一中学，江苏 江阴 214400； 2.江阴市教研室，江苏 江阴 214400）

物理思维的品质是衡量物理思维质量高低的指标，是物理能力形成与发展的重要因素.中学阶段，培养学生思维品质的一个重要方法就是解题教学.解题教学就是指在解题过程中，根据问题的不同特点，寻求合适的思维方式，从而达到解题目的的一种教学方式.在其过程中，通过引导学生对问题进行不同角度、不同方法等的全方面分析，进而达到培养他们思维品质的目的.下面就具体解题教学，看看如何培养学生的物理思维品质.

1 培养思维的缜密性

思维的缜密性是指思考问题的严密、有据.按照一定的逻辑顺序进行全面、周密的思考问题，审题时不但要注意明显的条件，而且要留意发现那些隐含条件，正确地使用概念，给出问题的完整解答，防止遗漏.在解题过程中培养学生全面剖析、不被表象所迷惑，不凭一知半解下结论的科学的求知品质是十分重要的.

例1.如图1所示，水平面上方区域充满着磁感应强度为B的匀强磁场，方向垂直纸面向里.一质量为m，带电量为＋q的小物块A沿水平面在匀强磁场中运动.物块运动的初速度v0，物块与水平面间的动摩擦因数为μ.若在该区域施加另一匀强电场E，使物块在磁场中恰能做匀速直线运动，那么该电场的方向怎么样？其大小为多少？

解析：通过受力情况可知此物块在未加电场时受到重力、洛伦兹力、摩擦力和支持力的作用，并且，洛伦兹力与重力同向，所以摩擦力大小为f＝μ（mg＋qv0B）.而要使物块做匀速运动，所加电场方向应水平向左，与摩擦力方向相反.则有qE＝f，即电场强度大小为一般情况下，很多学生到这里就认为解答完毕了，可从思维品质的角度来看，很多学生存在思维缜密性的缺陷，忽略了另一种可能存在的情况，即在电场力、重力、洛伦兹力作用下做匀速直线运动，即附加的电场方向也可以竖直向上，此时电场强度大小为

图1

2 培养思维的广阔性

思维的广阔性是指思维活动作用的范围及广度.它表现为思路开阔，能多方向、多角度去认识问题、分析问题和解决问题.在解题过程中，善于运用“变式”思维，对同一个问题进行多方位、多角度的思考，拓宽解题思路、解题途径，较好地理解和掌握所学的知识.

例2.如图2所示，在直角坐标系xOy内，有一质量为m、电量为＋q的电荷从原点O沿y轴正方向以初速度v0出发，电荷重力不计.现要求该电荷能通过点P（a，－b）.试设计在电荷运动的空间范围内加上“场”后并运用物理知识求解的一种简单、常规的方案.

（1）说明电荷由O到P的运动性质并在图中绘出电荷运动轨迹；

（2）用必要的运算说明你设计的方案中相关物理量的表达式（用题设已知条件和有关常数）.

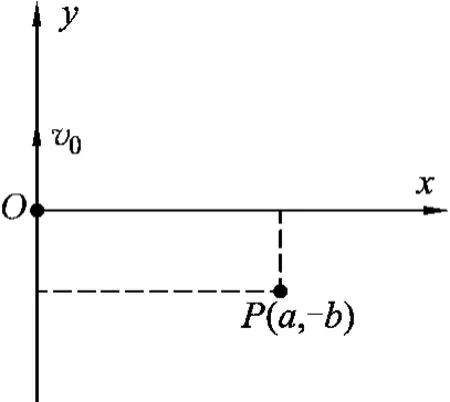
图2

图3

方案1.在x轴上O′点固定一带负电的点电荷Q，使电荷绕O′从O在库仑力作用下到P作匀速圆周运动，其轨迹半径为R，电荷的运动轨迹如图3所示.，由牛顿第二定律得

方案2.可以加一垂直纸面向外的匀强磁场，使电荷绕O′从O在洛伦兹力作用下到P作匀速圆周运动，其轨迹半径为R，电荷的运动轨迹如图4所示由牛顿第二定律得

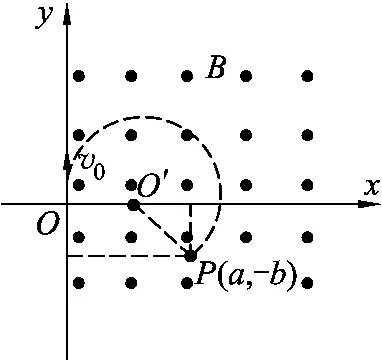
图4

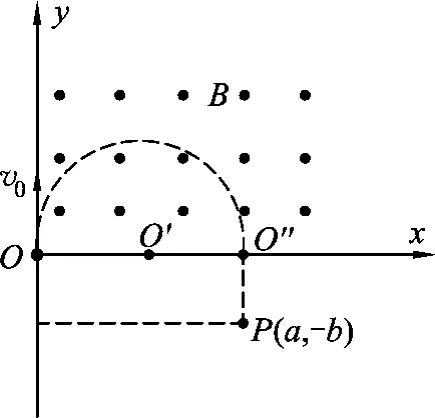
图5

方案3.可以施加一个x轴上方的有界磁场，使电荷绕O′从O在洛伦兹力作用下到O″作匀速圆周运动，然后作匀速直线运动到P，其轨迹半径为R，电荷的运动轨迹如图5所示由牛顿第二定律得

3 培养思维的深刻性

解题过程中能否透过表面现象看本质，是思维深刻与否的主要表现.很多的物理问题，条件关系比较隐蔽，如果只看问题的表面，是无从下手的.因此在物理解题过程中引导学生对疑难问题进行由表及里的思考，抓住问题的本质和规律，有利于学生迅速确定解题策略和组合各种有效的解题方法.

例3.如图6所示，在离坡底B为L的山坡上O点竖直固定一长也为L的直杆AO，A端与坡底B之间连接有一钢丝，钢丝处于伸直状态，若一光滑圆环从A点由静止开始无摩擦滑下，求圆环在钢丝上的滑行时间为多少？

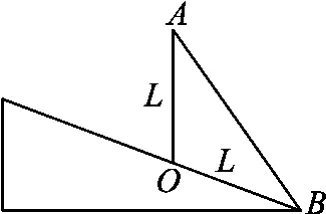
图6

解析：按照常规思维解决的话，该题似乎不知道坡底的倾角θ这一条件，导致无法求解.如果换个角度看问题，问题便迎刃而解，抓住本质特征AO＝BO＝L，即虚设一个等时圆，该等时圆以O点为圆心，L为半径如图7所示，则圆环从A至B的滑行时间等于从A至C的自由落体的运动时间，AC的长度为2L，由这道题的求解方法彰显了思维的深刻性，能够抓住题设中的AO＝BO＝L的本质特征，联想到A、B处在同一等时圆上，当然也彰显出了思维的灵活性.

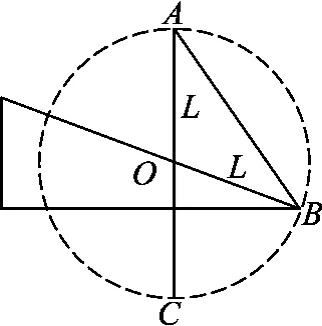
图7

4 培养思维的创造性

创造性思维是指完成思维活动的内容、途径和方法的独立程度.它集中表现为善于独立思考，思维不循常规，标新立异，用于创新.发展论认为：思维的创造性是一种不囿于常规，而又合乎逻辑规则的全新思维形式.培养学生这一优良的思维品质及创造思维的能力，是物理教学所要达到的思维训练的理想目标.在解题过程中引导学生根据已有的知识、经验和方法，对有关问题广泛联想，积极探索，大胆猜想，寻找合理方案解决问题.

例4.从地面上以初速度v0竖直向上抛出一个质量为m的小球，若运动过程中受到的空气阻力与其速率成正比关系，球运动的速率随时间的变化规律如图8所示，t1时刻到达最高点，再落回地面，落地时的速率为v1，且落地前已经做匀速运动.求小球上升的最大高度？

解析：（1）微元法.此题受2008、2009年江苏高考的影响，对微元法的重视程度已经达到了一定的境界.对上升过程的某一极短时间内.对等式两边分别求和，可得落回地面过程中，由题意有

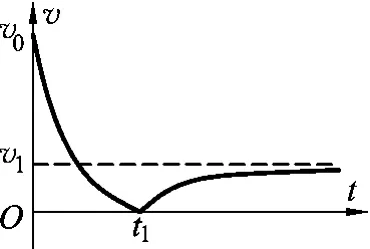
图8

（2）运用动量定理解题.此种解法从某种意义上来讲具有一定的创造价值，与速度成正比的力称为正比例线性力，如f＝kv.当力与速度共线时，力在一段时间内Δt内的平均值为¯f＝k¯v，则其冲量为¯f·Δt＝k¯v·Δt＝k·s，这表明与速度共线的正比例线性力的冲量跟位移成正比.对上升整个过程利用动量定理：以竖直向上为正，则有－mgt1－kH＝0－mv0，mg＝kv1，所以

5 思维的变通性

对于一些按照常规思维难以解决的问题，如果换个角度看问题，思路可能会豁然开朗.然而，有没有换个角度看问题的意识与能力，正是“专家”与“新手”解决问题的主要差异.从思维的品质来看，善于换角度分析问题则反映了人的思维变通性的高低.

例5.一位电脑动画爱好者设计了一个“猫捉老鼠”的动画游戏.如图9所示，在一个边长为a的大立方体木箱的一个顶角G上，老鼠从猫的爪间逃出，选择了一条沿着木箱的棱边奔向洞口的最短的路线，洞口处在方木箱的另一顶角A处，若老鼠在奔跑中保持速度大小v不变，并不重复跑过任一棱边及不再回到G点.聪明的猫也选择了一条最短的路线沿木箱表面奔向洞口（设猫和老鼠同时从G点出发），则猫奔跑的速度为多大时，猫恰好在洞口再次捉住老鼠？

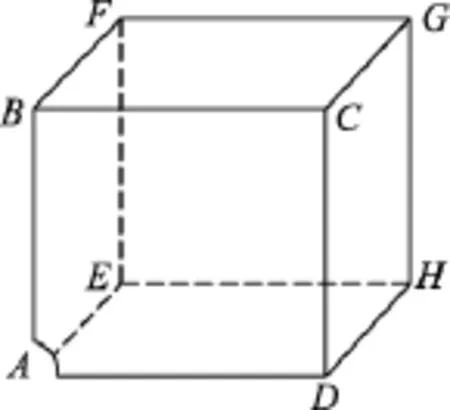
图9

解析：此题也看似无从下手，但如果跳出物理思维的框框，运用数学思维则是一个不错的选择，彰显了思维的变通性.如图10所示，在正方形ABCD 中，沿 AB、CD、AD三边剪开，然后把正方形ABCD绕BC轴向上翻转90°，A点变成J 点，连接GJ，交BC于I，然后再连接AI，则猫沿着GI、IA路线跑，路径最短，因为GJ最短，理由是在三角形中，两边之和大于第三边.猫走的最短路程老鼠从顶角G点出发，走过的最短路程x＝3a.由题意可知：由于猫与老鼠同时抵达洞口A，有，所以猫的速度

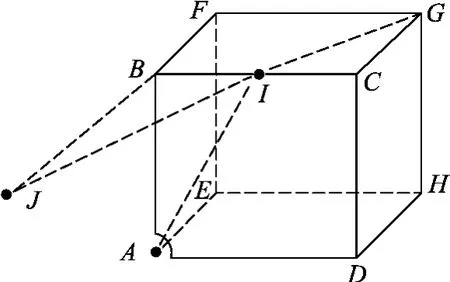
图10

6 思维的批判性

批判性思维就是要突破框框，“离经叛道”.批判性思维是理性的思维、反思性的思维.发展批判性思维可使学生增强区分真理与谬误的能力，不轻信盲从，有检查和评价的意向，能及时纠正错误，是培养学生良好思维品质的重要途径.因此，在解题教学中应鼓励学生大胆提出自己的看法，养成良好的批判性思维习惯.

例6.如图11所示，固定的水平光滑金属导轨，间距为L，左端接有阻值为R的电阻，处在方向竖直向下，磁感应强度为B的匀强磁场中，质量为m的导体棒静止在导轨上，导轨与导体棒的电阻均可忽略.现给导体棒水平向右的初速度v0.导体棒始终与导轨垂直并保持良好接触.求：导体棒在导轨上移动的最大距离x.

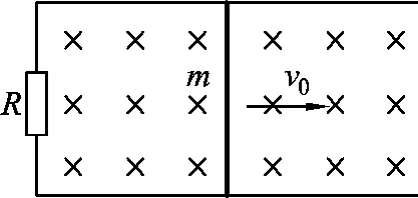
图11

这时，教师可以针对这位学生的答案向学生提出这样的问题：此种解法完美吗？如果不完美，说明理由并证明之（还是渗透微元法）.

不完美之处在于解答中并没有证明安培力是随位移成线性关系，现证明如下.

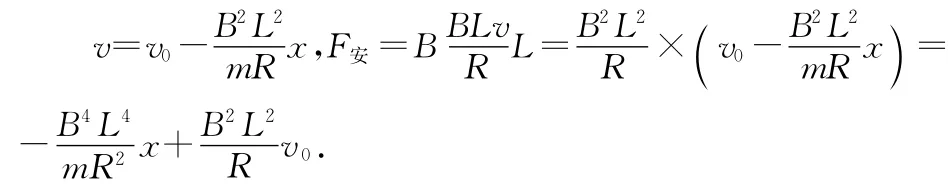
F安与导体棒位移x成线性关系.在学生解决问题的过程中，他们对公式的适用范围会有更准确的理解，同时也能够让学生灵活地掌握好重要的物理方法——微元法.

（注：熟悉微元法的读者，可用微元法很快解出该题）

由于思维品质的几个方面是有机联系的，密不可分的，因此对他们的培养也是相互依存的，互相促进的.如何在物理解题教学中培养学生的物理思维品质，对于我们来说还是一个新的课题，有待于在今后的教学实践中进一步研究.