文丘里高压湿气测量虚高特性数值模拟

徐 英，段玉晗，赵 轶

(天津大学电气与自动化工程学院天津市过程检测与控制重点实验室，天津 300072)

湿气是气液两相流动的一种特殊形态，在自然界及工业生产过程中普遍存在．关于湿气流量测量的方法种类较多，其中，研究时间最长、影响最深远的为基于节流式的湿气测量方法．该方法始于20世纪中叶，近 60年来，国内外众多研究者进行了大量的理论与实验研究工作，并针对不同节流装置及工况得出了形式各异的虚高测量模型．比较经典的有Homogenous 模型[1]、Murdock 模型[2]、Chisholm 模型[3]、De Leeuw 模型[4]和 Steven 模型[5]等．由于这些模型所基于的实验介质、实验条件、节流装置形式等各有不同，其通用性往往较差，使用时需要根据具体情况加以修正．利用 CFD方法进行一定规模的有效数值模拟实验，在此基础上结合少量的实流实验，不仅能够加快工作进程，实现结构的优化，而且可以大大降低实流实验所需要的装置工程建设、样机加工制作、动力能源、实验介质等方面的成本，因此探索仿真对实流实验的预测方法、提高预测准确度是一项重要且有实际意义的工作．国内外对差压式流量计的仿真研究和应用表明，当网格划分良好、计算模型与仿真方法适当时，是能够有效预测实流实验并指导流量传感器结构优化设计的[6-10]．笔者对标准文丘里管高压湿气虚高特性进行了数值模拟，给出了湿气仿真方法，并利用英国国家工程实验室(National Engineering Laboratory，NEL)关于标准文丘里管高压湿气实验结果作为仿真验证的参比数据．

1 湿气虚高的含义与影响因素

1.1 虚高的含义

利用节流装置进行湿气流量测量时，由于液相的存在，差压值比单独等量气体流过时偏大，测得的流量值偏高，即产生虚高现象，虚高通常定义为

式中：tpW为湿气质量流量；tpΔp为湿气差压值；pΔp为等量干气质量流量gW流过时的差压值．

1.2 湿气虚高特性的影响因素

理论与实验研究表明，差压式流量计的湿气虚高特性主要受 4因素的影响[11]：液相质量含率、气相Froude数、工作压力和直径比 β．对于标准文丘里，直径比 β为喉部直径与上游取压口平面处圆筒段的内径之比．液相质量分数通常用 Lockhart-Martineli参数表示，(记为 X)，是对气液两相流中液相质量分数的非空间描述，表达式为

式中：lW、gW分别为液、气质量流量；gρ、lρ分别为气相、液相密度．

Froude数为表征气体惯性力与重力之比的无量纲相似准则数，反映了气体的表观速度、气液密度、管道内径等诸多因素的内在联系，即

式中Usg为气相表观速度，m/s，其表达式为

式中D为管道内径．

2 文丘里高压湿气实验工况

为保持仿真实验最大程度的模拟实流实验，将仿真实验工况设定为与文献[5]基本相同，如表 1所示，压力为 2,MPa、4,MPa和 6,MPa，每一压力下的气相流量为 400,m3/h、600,m3/h、800,m3/h和 1,000,m3/h，每一气相流量下又设计若干个液相流量实验点，最大液相流量如表 1中所示，用 W1max指示，实流实验没有给出具体的液相流量实验点，仿真实验中液相流量将0～W1max之间平均分配了10等分．

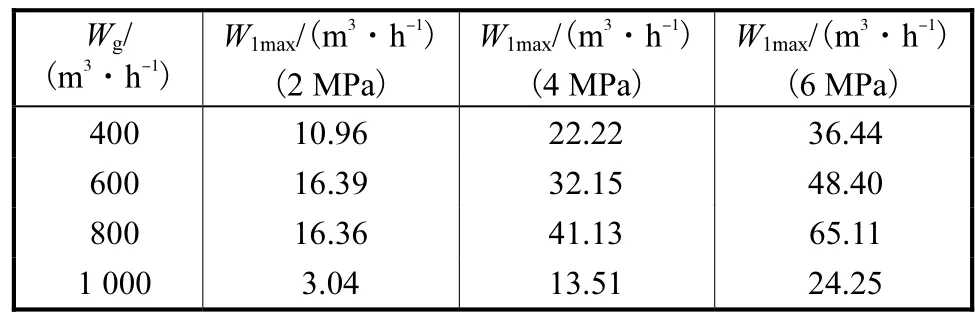
表1 3个压力下最大液相流量Tab.1 Maximal liquid flowrates under three pressures

仿真实验节流装置的几何模型与文献[5]中测试样机在结构参数上完全一致．文献[5]研究中采用ISA,Controls公司的标准文丘里管，管径15.24,cm，直径比0.55，温度为300,K．仿真介质与实验介质相同，连续相为氮气，离散相为煤油．由于液体的不可压缩性，仿真中根据常压设定密度与黏度参数；气体根据压力和温度的不同设定相应的密度、黏度等参数．

NEL实验数据经处理后得Lockhart-Martinelli参数与虚高的关系，文献[5]中图5～图8已详细给出．本研究将以此为参比数据源，利用 CFD的离散相模型(discrete phase model，DPM)，通过数值仿真方法预测文丘里高压湿气虚高规律，并将虚高预测值与NEL实验结果相比较．

3 高压湿气仿真实验方法

3.1 湿气仿真计算模型

标准 k-ε模型是目前使用最广泛的湍流模型，而经过模型适应性比较研究，发现重正化群(renormalization group，RNG) k-ε模型在本实验比标准模型有更好的精度，故仿真工作选用 RNG k-ε模型．边界条件采用质量入口和压力出口．

当连续相的体积含气率近似大于 90%的两相流动，可以使用离散相模型离散相实现流场的计算．文献[5]中的实验工况体积含气率大于 91.2%，因此在湿气仿真中使用离散相模型．

3.2 仿真实验步骤

湿气仿真采用先计算连续相流场，连续相流场收敛后，再计算离散相的方法．本研究中标准文丘里管直径比固定为0.55；气相折算速度和工作压力均在连续相的计算中设置；在离散相设置中只改变液相质量含率．对同一个计算完成的连续相流场中分别添加质量流速不同的液相，相当于固定气相Froude数、工作压力和直径比β 3个参数，而只考察液相质量含率对虚高的影响．此外，还依据工作压力和气相流量，构造并计算出不同的连续相流场，并随后向它们中添加液相．这样，又能将气相 Froude数、工作压力参数的影响考虑进来．

仿真实验3个工况压力，每个工况压力下计算了4个气相流量点，每个气相流量点下改变液相质量流量10次．

4 仿真实验结果

对仿真计算结果进行处理，根据文献[5]中图 5～图8形式，给出高压工况下标准文丘里管仿真预测的虚高值与 Lockhart-Martineli(X)关系，如图 1所示，分析如下．

(1) 其他条件相同时，仿真虚高值随液相含率的增大均呈现明显的单调上升趋势．

(2) 根据表 1，气相工况流量在 1,000,m3/h时，由于液相流量实验设定值较低，即压力一定时，实验为大气量与小液量的配比，仿真结果虚高值相对较低，小于 1.15．理论上，大气量与大液量配比会导致虚高值增大，由此推测 NEL开展实验时受到了实验装置能力的限制．

(3) 工况压力为 2,MPa时，各气相流量的虚高数据分散度较小，只有少数点(X分别为0.1和0.135)出现了向下偏离的现象．

(4) 工况压力为4,MPa时，气相流量为800,m3/h的虚高值相对偏小，400,m3/h与600,m3/h的趋势基本一致．

(5) 工况压力为6,MPa时，除2个点外，即当X为 0.28时，气流量为 800,m3/h的点和 X＝0.32时400,m3/h的点出现了向下偏离的现象，其余数据呈现一定重合性．

(6) 由各压力下的虚高数据汇总发现(见图 1)：压力增大，虚高值相应减小(个别点例外)．工况压力对虚高的作用主要体现在压力对气体密度的影响，压力越大，气相密度越高，气液两相间的速度滑差越小，气液两相间的摩阻越小，在理想的极端情况下，当气体密度和液体密度相等时，气液两相具有相同的惯性力，流速一致，气相对液相将不产生加速作用，气液两相间也将不存在摩阻．因此工况压力的增大使得气液两相间的摩阻减小，在其他条件不变的情况下，气液两相间摩阻减小，虚高将减小．

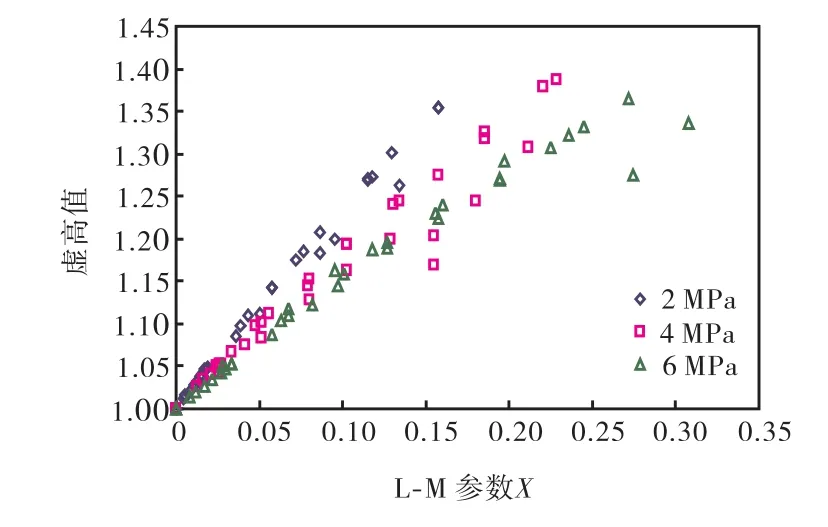
图1 各压力仿真实验虚高特性Fig.1 Overreading characteristic by simulation under individual pressures

5 仿真实验与实流实验结果比较

根据前面仿真结果分析，除个别点外，在相同的Lockhart-Martinelli参数下，文丘里管的虚高值随着压力的增加而减小，与实流实验趋势相一致．但是，实流实验虚高的最大值在 1.45左右，而仿真实验的虚高最大值略小于1.4，仿真实验存在一定预测误差．

5.1 实流实验数据拟合公式误差

为了将仿真实验计算结果与实流实验进行定量对比，利用图形数据化软件GetData将实流实验图中的点量化为具体数据值(受原始图形像素质量的限制，数据获取结果会存在一定偏差)．为实现定量比对，将 3个压力下的实流实验数据分别进行拟合，得到虚高与 Lockhart-Martinelli参数之间的函数模型Φr(X)．图 2即为实流实验数据的拟合公式误差散点图，基本在±3%以内．

5.2 仿真与实流实验虚高的比较

由于仿真实验设计的工况条件与实流实验并不是完全对应的，如表1中，实流实验液相在0～W1max之间给定，本研究利用图形软件获取其具体数据，而仿真实验是在0～W1max区间进行了10等份，因此不能采用点对点一一对比的方式进行比较．比对方法是将仿真实验 X参数代入实流实验虚高拟合公式Φ(X)中，由此计算得到的实流实验虚高值作为仿真的参比标准，以此评估仿真实验的虚高预测误差．

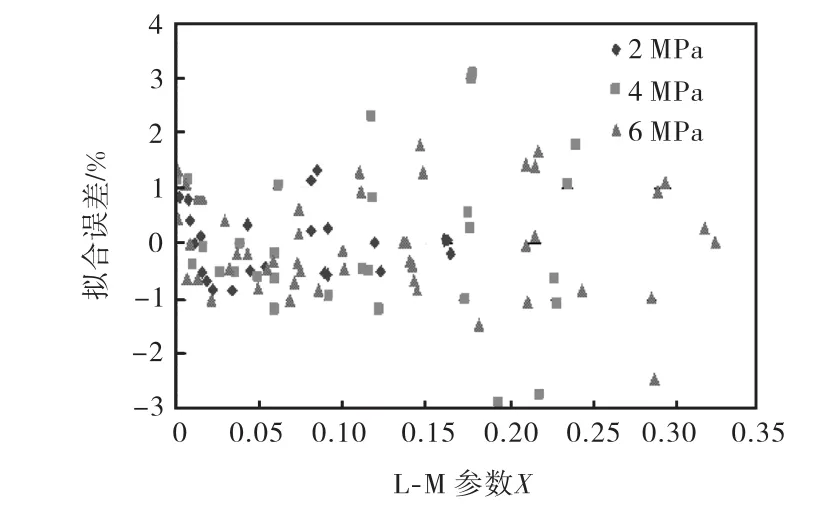
图2 实流实验数据拟合误差散点分布Fig.2 Scattered fitting error for experimental data

图 3～图 5为实流实验与仿真实验虚高值的对比．可以看到，各压力下仿真与实流实验虚高值随 X参数的变化趋势基本一致，总体上，实流实验虚高值略高于仿真值，表明仿真方法在一定程度上存在所谓的“系统偏差”．

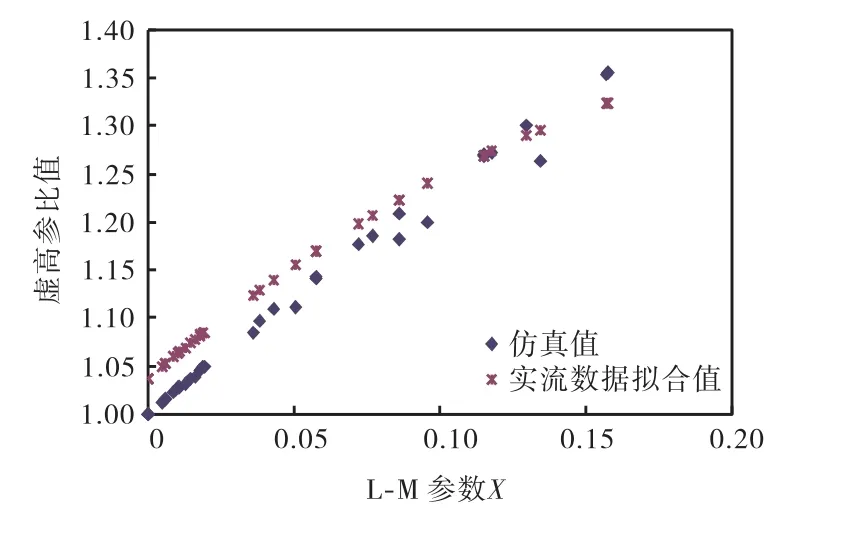
图3 2,MPa仿真与实验值的比较Fig.3 Comparison between simulation and experimental data at 2,MPa

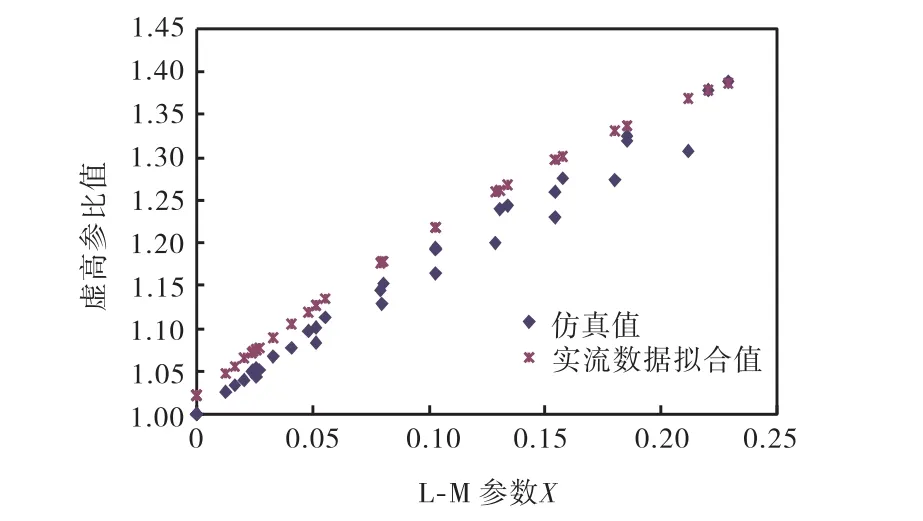
图4 4,MPa仿真与实验值的比较Fig.4 Comparison between simulation and experimental data at 4,MPa

5.3 仿真实验虚高误差

仿真与实流实验虚高值之间的相对误差值定义为

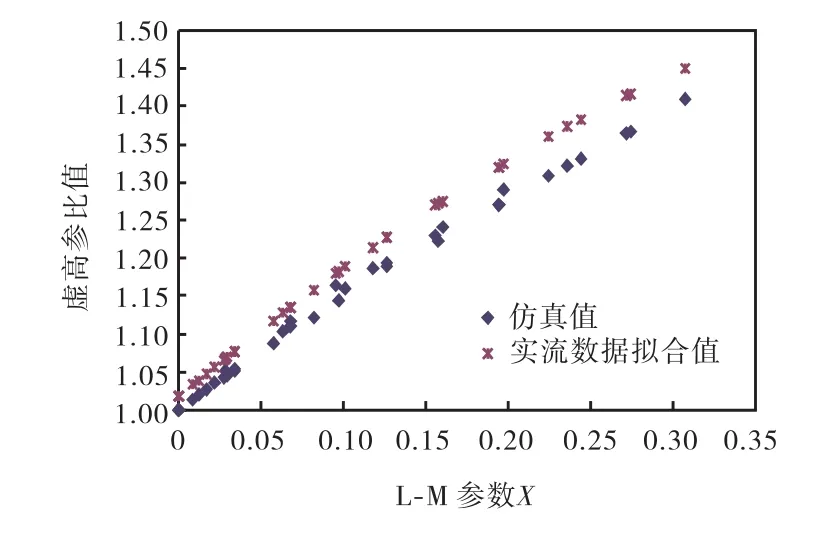
图5 6,MPa仿真与实验值的比较Fig.5 Comparison between simulation and experimental data at 6,MPa

式中：Ep为仿真虚高值的相对误差；Φs为仿真实验虚高预测值；Φr为相同X下的实流实验虚高值．不同压力下仿真实验虚高预测误差如图6所示，除 2,MPa压力下少数点呈现正偏外，其余误差均为负偏．误差绝对值的最大与平均统计结果如表 2所示．可以看到，对高压下标准文丘里管虚高特性进行数值模拟的虚高值最大相对误差为 5.14%，平均相对误差小于2.8%．

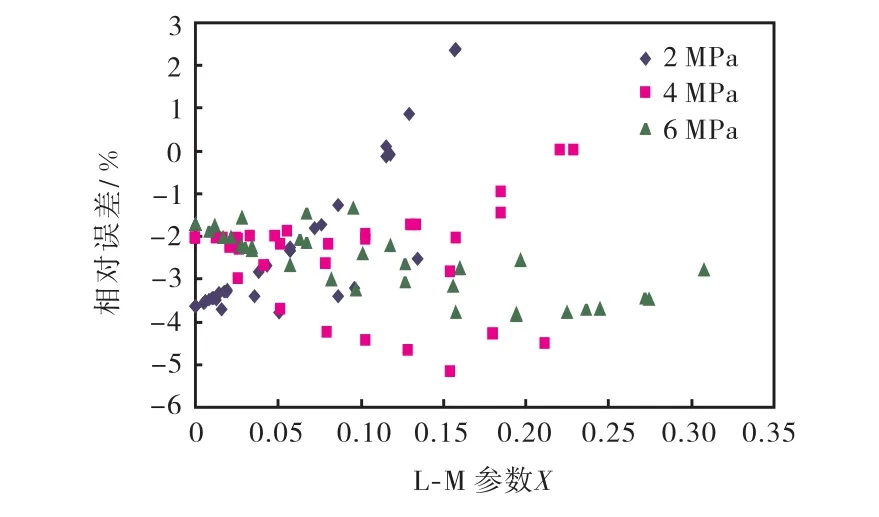
图6 仿真实验虚高预测误差汇总Fig.6 Errors of overreadings by simulation under individual pressures

表2 仿真Ep,max和EpTab.2 Ep,max，Ep by simulation

5.4 误差来源分析

仿真实验中误差产生的原因主要有3个方面．

(1) 获取实流实验数据源的方法存在一定误差．实流实验源数据的获取利用了图形数字化软件GetData，数据图片本身的像素质量在一定程度影响了参比数据的准确性．

(2) 仿真本身存在对模拟流动的简化．首先，FLUENT 中的离散相模型假定第二相(离散相)非常稀薄，因而颗粒-颗粒之间的相互作用未加以考虑．其次，仿真中的曳力模型、升力模型等，都是对实际情况的近似模拟，与实际情况不尽相同．例如，在仿真中理想化地认为颗粒形状为球形，这将对曳力的计算产生影响．

(3) 仿真实验离散相粒子轨迹举例如图 7所示(压力为 2,MPa，气相流量为 400,m3/h、液相流量为10.96,m3/h)．图中(A-A)、(B-B)、(C-C)，…，(M-M)截面分别给出了不同截面粒子的分布信息．差压取压点为(B-B)、(G-G)所在平面．观察(G-G)截面，发现离散相颗粒密度不再是均匀分布，而是出现内壁附近颗粒密度下降，中心区域密度增大，故由取压点处所得的压力受离散相的影响减小，导致此处压力偏大，B-B至G-G差压减小，使得仿真虚高整体偏小．

图7 仿真实验离散相粒子轨迹图(p＝2,MPa，Wg＝400,m3/h，Wl＝10.96,m3/h)Fig.7 Particle tracks of discrete phase model by simulation(p＝2,MPa，Wg＝400,m3/h，Wl＝10.96 m3/h)

6 CFD虚高预测模型及与经典模型预测结果的比较

6.1 CFD虚高预测模型

在仿真数据的基础上给出标准文丘里管高压状态下湿气虚高的预测模型．在相同的工况压力下，Lockhart-Martinelli参数对虚高值具有主导影响，而气相流量的变化对虚高影响相对较小．因此，虚高建模只考虑液相含率对虚高的影响作用．对图 1分析，发现Lockhart-Martinelli参数和虚高值之间呈现近似线性的关系，在 Lockhart-Martinelli参数较大时，虚高值上升速率有所减缓，采用一简单的二阶曲线拟合即可满足其函数关系．不同工况压力的虚高预测模型如式(6)所示，其中 Φs-g1、Φs-g2、Φs-g3分别表示 2 MPa、4 MPa、6 MPa下的虚高．

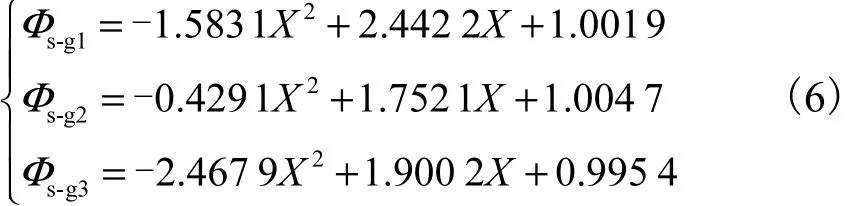
6.2 与经典模型预测结果的比较

6.2.1 预测气相流量误差

研究湿气流量测量的目的是获得气液两相尤其是气相的流量数据．因此，给出虚高模型后，最终要通过气相流量的预测是否准确来评判模型的质量．笔者将仿真模型(用 TJU-CFD 表示)、Steven模型以及Murdock1.26、Murdock1.5、Chisholm、Lin(林宗虎模型)、De Leeuw、Homogenous模型等经典模型对气相流量的预测结果进行对比，误差定义为

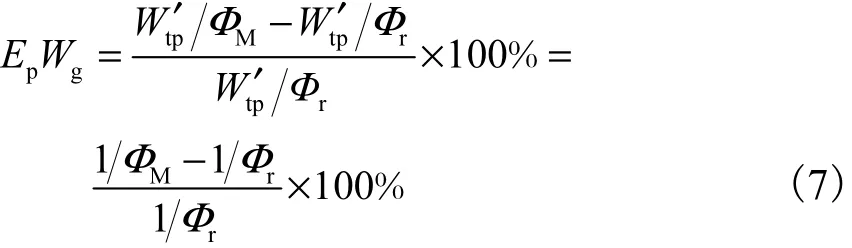
式中：tpW′为参比实流虚高流量；rΦ与式(6)中定义相同；MΦ表示相同工况条件下不同虚高模型给出的虚高值．

6.2.2 各模型误差比较

图 8～图 10给出了 3个压力下 CFD虚高模型与各经典虚高模型的误差比较结果，横轴为干度，纵轴为模型误差．干度为气液两相中气相质量流量所占两相总质量流量的份额，用x表示．从图8～图10中看到，各虚高模型的误差都随干度的增大而减小，大致规律如下：

(1) Steven模型误差值均在±3%以内．由于该模型直接利用 NEL实验数据拟合给出[5]，毫无疑问具有最高的精度．

(2) 基于仿真实验的 TJU-CFD 模型，只在压力为 4,MPa时，个别点误差超过 5%，其余均在±3%以内．

(3) Homogenous模型和 De Leeuw模型[3]预测误差较小，基本在±5%以内．

(4) Lin(林宗虎模型)[12]在干度较小的情况下，预测值偏高，突出问题是干度接近 1时，出现负误差，即使在纯干气的情况下，预测误差值也没有回归到0附近．

(5) Murdock1.5模型，干度小于 0.8时，2,MPa和4,MPa基本误差均大于5%，最高到了10%；6,MPa时，误差基本在5%以下．

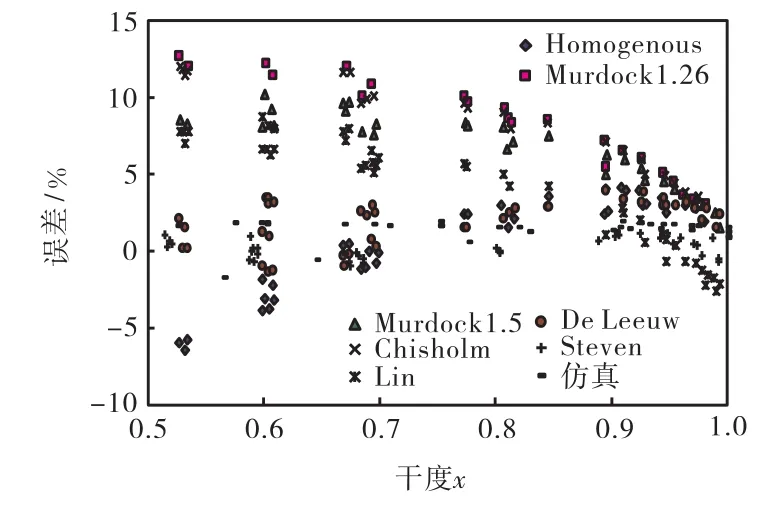
图8 2,MPa各模型气相流量预测误差Fig.8 Predicted errors of gas flow rates for individual models(2 MPa)

(6) 各压力下，Murdock1.26模型预测整体偏高，干度约小于 0.8时，2,MPa和4,MPa压力下误差均大于 7%，最高超出 10%；6,MPa压力时，干度在0.85以上，误差大致在3%～5%之间．

(7) 总体上，Chisholm 模型较 Murdock1.26模型误差更高．

各模型平均相对误差E与最大相对误差 Emax比较及排序如表 3所示．TJU-CFD模型最大误差

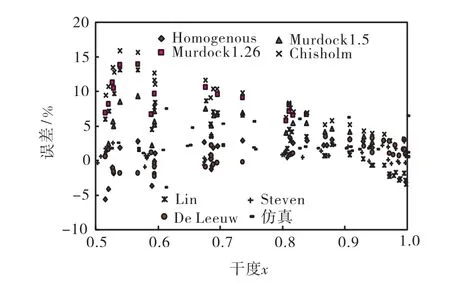
图9 4,,MPa各模型气相流量预测误差Fig.9 Predicted errors of gas flow rates for individual models(4,MPa)

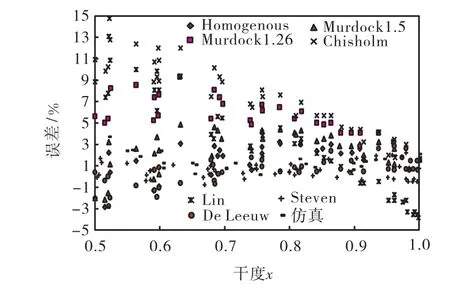
图10 6,,MPa各模型气相流量预测误差Fig.10 Predicted errors of gas flow rates for individual models(6,,MPa)

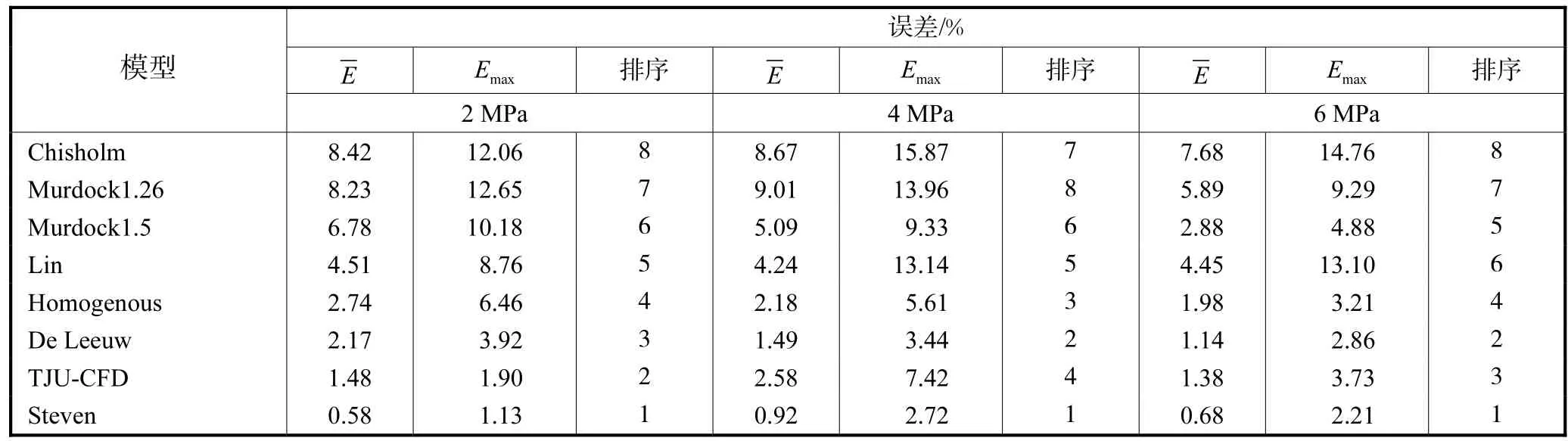
表3 各模型比较及排序Tab.3 Comparing and ordering of individual models

7.42 %，平均误差为2.5%，分别在2,MPa、4,MPa、

6,MPa压力下预测能力依次排序为第 2、第 4和第 3位．4,MPa下与排序第 3的Homogenous模型接近，平均误差为 2.58%；在 6,MPa下与排序第 2的De,Leeuw模型接近，误差仅为1.38%．

7 结 论

(1) 给出了基于离散相模型的湿气数值模型方法与仿真计算流程，证明了该方法能够有效预测高压工况下标准文丘里管的虚高．

(2) 通过对标准文丘里仿真预测虚高与NEL实流实验参比虚高数据的比较，得到预测虚高最大相对误差为5.14%，平均相对误差小于2.8%．

(3) 根据仿真实验数据拟合出虚高预测模型，与Steven模型及 6个经典模型(Chisholm模型、Murdock1.26模型、Murdock1.5模型、林宗虎模型、Homogenous模型、De Leeuw模型)的流量预测值进行了比较．3个压力下与其他模型比较，仿真模型预测能力排序依次为第 2、第 4和第 3位，最大相对误差小于7.5%，平均误差为2.5%．

［1］ 阎昌琪. 气液两相流[M]. 哈尔滨:哈尔滨工程大学出版社，2007．Yan Qichang. Gas Liquid Two Phase Flow[M]. Harbin:Harbin Engineering University Press，2007(in Chinese)．

［2］ Murdock J W. Two-phase flow measurement with orifices[J]. Journal of Basic Engineering，1962，84(4)：419-433．

［3］ Chisholm D. Void fraction during two-phase flow[J].Journal of Mechanical Engineering Science，1973，15(3)：235-236．

［4］ De Leeuw H. Liquid Correction of Venturi Meter Readings in Wet Gas Flow[R]. Kristiansand：North Sea Flow Measurement Workshop，1997.

［5］ Steven R N. Wet gas metering with a horizontally mounted Venturi meter[J]. Journal of Flow Measurement and Instrumentation，2002，12：361-372.

［6］ Barton N. CFD Techniques Applied to Differential Pressure Flow-Meter Performance[R]. Glasgow：National Engineering Laboratory，1999.

［7］ Ekambara K，Sanders R S，Nandakumar K，et al. CFD simulation of bubbly two-phase flow in horizontal pipes[J]. Chemical Engineering Journal，2008，144(10)：277-288.

［8］ 徐 英，吴经纬，杨会峰，等. 内锥流量计流出系数预测方法研究[J]. 计算力学学报，2009，26(5)：727-733.Xu Ying，Wu Jingwei，Yang Huifeng，et al. Predicting discharge coefficient of V-cone flowmeter with four turbulence models[J]. Chinese Journal of Computational Mechanics，2009，26(5)：727-733(in Chinese).

［9］ 吴经纬. 内锥流量计可膨胀系数与湿气测量特性的实验研究[D]. 天津：天津大学电气与自动化工程学院，2007.Wu Jingwei. Numerical Research of Wafer Cone Meter on Its Expansibility Factor and Characteristics of Wet Gas Metering[D]. Tianjin：School of Electrical Engineering and Automation，Tianjin University，2007(in Chinese).

［10］ National Engineering Laboratory. The Evaluation of Wet Gas Metering Technologies for Offshore Application：Part1-Differential Pressure Meters[R]. Glasgow：National Engineering Laboratory，2003．

［11］ 王 帅．DPM 模型的基本操作和注意事项[J]．数值计算与工程仿真，2005，1(4)：37-41.Wang Shuai. Basic operation and precautions of DPM[J]. Numerical Calculation and Engineering Simulation，2005，1(4)：37-41(in Chinese)．

［12］ Lin Zonghu. Two-phase flow measurements with sharpedged orifices[J]．International Journal of Multi-Phase Flow，1982，8(6)：683-693．