基于免疫进化算法的发动机悬置系统稳健优化

2012-07-19张旭

汽车科技 2012年5期

张旭

（合肥工业大学交通运输工程学院，合肥 230009）

发动机不平衡惯性力和转矩波动是引发汽车振动和噪声的一个最主要振源，是降低乘坐舒适性的主要原因。发动机悬置系统除支撑发动机和变速器等部件外，还隔离发动机振动向车架的传递，并减轻路面与轮胎对车身激振所引发的动力总成振动［1］。因此，悬置系统设计的优劣直接关系到发动机振动向车体的传递，影响整车的NVH性能。发动机悬置系统的优化设计旨在合理选择悬置参数(如安装位置、角度、刚度和阻尼等)，以有效降低整车振动及噪声水平，并且保证由于各种可控和不可控因素的影响发生微小变差时，都能保证悬置系统的稳健性［2、3］。

将稳健设计思想应用于发动机悬置系统的解耦优化设计中，基于悬置系统振动解耦的能量分布建立优化目标函数，以悬置刚度参数为设计变量，根据整车性能要求添加约束，综合运用遗传算法、免疫进化算法，对悬置系统进行优化，同时利用Monte Carlo方法进行稳健分析。

1 发动机悬置系统数学模型

将车架和动力总成视为刚体；假定橡胶件的弹性是线性的，并可忽略不计其阻尼，建立如图1所示的六自由度动力总成四点悬置模型［4］。

图中O-XYZ为发动机动力总成质心坐标系，O为动力总成质心，X轴平行于发动机曲轴轴线指向发动机前端，Z轴通过发动机总成质心竖直向上，由右手定则得出Y轴；前悬置点1、2，后悬置点3、4；u、v、s为悬置的3条弹性主轴方向。则可得广义坐标 q={x，y，z，θx，θy，θz}。

由拉格朗日方程可以得到悬置系统的振动方程为：

式中：M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；q为广义坐标；F（t）为系统所受的激振力。

方程可简化成：

由式（2）可得动力总成悬置系统的固有频率ωj（j=1，2，3，4，5，6）和固有振型 φ。

2 能量解耦法

通常六自由度汽车动力总成悬置系统的6个固有振型在多个自由度方向上是耦合的，在某个自由度方向受到激振都可能引起耦合振动，这样会导致共振频带加宽，共振的机会加大。能量解耦法是在得到悬置系统的6个固有模态后，根据能量分布判断动力总成悬置系统是否解耦及其解耦的程度，然后通过修改悬置参数提高系统在某些方向上的解耦率［5，6］。

当系统以第j阶模态振动时，定义能量分布矩阵的第k行l列元素为：

式中：k，l，j=1，2，3，4，5，6；φ（k，j）、φ（l，j）分别为第 j阶振型的第k个和第l个元素；M（k，l）为系统质量矩阵的第k行、第l列元素；ωj为第j阶固有频率。

当系统以第j阶模态振动时，第k个广义坐标分配能量占系统总能量的百分比为：

若 Qa（j，k）=100%，则系统做第 j阶振动时能量全部集中在k对应的广义坐标上，此时该模态振动完全解耦。

3 优化模型

3.1 优化方法

考虑到在实际的生产与使用过程中悬置垫参数都有很大的可变性，在悬置参数的优化设计中需要结合稳健设计的思想，免疫进化算法既保证最优解的高解耦率，还能保证最优解的可行稳健性。算法流程图如图2所示。

遗传算法的编码方式采用所有变量的二进制编码串起来，组成24×n的二进制串，变异操作时分为三类，变异概率分别为 0.00，0.08，0.45，记忆种群中解的个数为20，进化代数为60。

3.2 设计变量

综合车架和动力总成设计限制，本文以悬置点处悬置橡胶的各向主刚度值 K=（k1，k2，……，kn）（n为悬置刚度个数）为设计变量。

3.3 约束条件

（1）刚度约束：既要限制发动机的位置移动;又要使系统具有较好的隔振性能，即Kimin≤Ki≤Kimax（i=1，2，…n）。

（2）频率约束：悬置系统的最大固有频率须小于发动机自身激励频率f的为了避开路面激励频率，悬置系统最小频率应大于5 Hz；各阶频率之间间隔应大于 0.5 Hz。

3.4 目标函数

作者以实现悬置系统六自由度能量解耦最大为目标进行优化设计。优化函数为：

式中：Qi为各自由度能量百分比；αi为加权因子。

3.5 优化实例

针对某款客车，发动机为六缸四冲程。四点悬置，平置式，对称分布。客车动力总成参数如表1所示，各悬置点主刚度值如表2所示。

表1 动力总成系统参数表

由以上数据可计算出该悬置系统的6个固有频率和各频率下的能量矩阵，如表3所示。

表3 优化前悬置系统固有频率和能量分布

根据表3中的数据可以看到，悬置系统固有频率满足频率约束条件，但是一阶与二阶固有频率间隔小于0.5。从能量分布上来看，除横向（y）自由度外，其余各自由度方向能量分布小于80%，各自由度之间存在严重的振动耦合。

采用免疫进化算法对以上悬置系统在matlab环境下进行稳健性优化设计。从最终的记忆种群中提取最优解结果并计算其固有特性，如表4、表5所示。

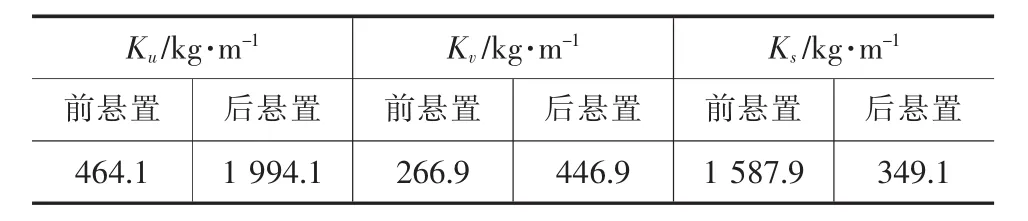
表4 优化后各悬置点主刚度值

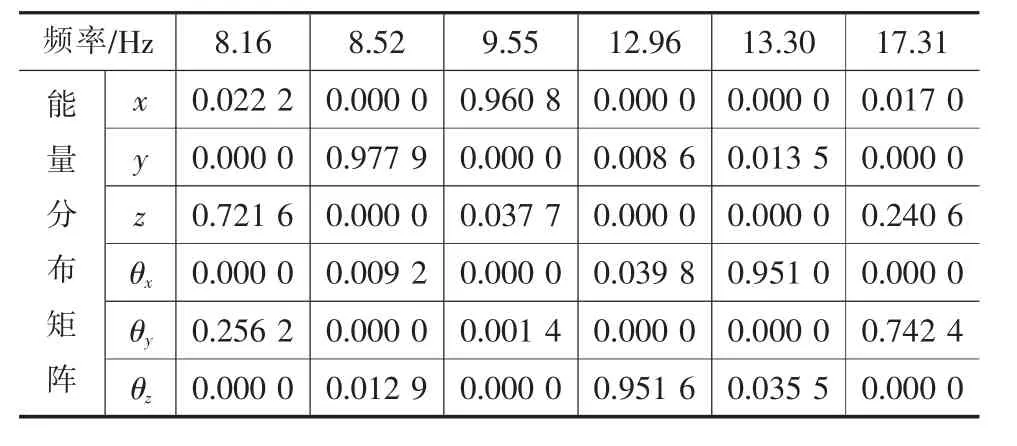
表5 优化后悬置系统固有频率和解耦率

由表5可知，最优解的频率都在合理的频率约束的范围内，且间隔都大于0.5。各自由度上的能量分布，除了垂向（z）与俯仰（θy）方向分布较低外，其余自由度能量分布均大于95%。与原系统相比，在六个自由度上的振动能量分布均有显著提高，且平均提高 18.3%。对于垂向（z）与俯仰（θy）自由度还可以通过改变悬置系统各悬置点的位置以及悬置安装角大小进一步优化。

4 基于Monte Carlo的稳健分析

在一系列生产与使用一段时间后的悬置垫样品中随机抽样检测发现，各向悬置主刚度基本上在±12%范围内波动，且分布曲线成正态分布。建立优化目标函数的响应面模型，以各向主刚度为服从正态分布相互独立的随机变量。优化前的悬置刚度变量分布为：U1～N（453，54.362），经过 2 000 次随机实验分析，通过计算可以得出响应面模型的概率分布为：P1～N（2.4859，0.80612），目标函数的标准差为32.43%。

根据设计要求，设计变量出现随机变化时其产品性能变化最好不超过5%，此响应面的变化明显超出了允许值，稳健性较差。

对优化后悬置系统分析，经过2 000次随机实验分析，响应面模型的概率分布为：Q1～N(0.856 1，0.023 82），标准差分别为：2.78%，小于允许值，效果明显。优化前后响应面模型概率分布和响应面拟合正态曲线分别如图3、图4所示。

采用Monte Carlo方法分别对优化后的六个自由度上的解耦率建立响应面模型进行分析，其目标函数是基于单自由度解耦率建立的，消除彼此的影响，其响应面模型概率分布如图5所示。

计算可得，图5所示的各自由度解耦率所构成响应面模型的标准差分别为：0.94%、0.6%、0.36%、3.13%、0.6%、3.17%，各自由度都有很高的稳健性。