单相三电平PWM整流器电流解耦控制方法

黄嘉鹏，张 斐

（西南交通大学 电气工程学院，四川 成都 610031）

0 引 言

与传统不控整流或相控整流方式相比，PWM整流方式具有功率因数高、可实现能量双向传输等优点，是一种真正的“绿色”电能变换［1］。

PWM整流器的控制目标包括网侧输入电流和直流输出电压，且主要根据输入电流正弦度以及是否与输入电压同频同相位来评估整流器性能的优劣。然而由于网侧输入电压波动，PWM整流器的电流控制器设计困难。直流功率变换器可以设计实现无稳态误差的电流控制器，但若交流功率变换器采用同样的设计方法，网侧输入电流幅值和相位均会产生较大的稳态误差［2］。

文献［3］通过引入一个虚拟输入电流，提出了单相三电平PWM整流器基于dq坐标系的电流控制策略，但电流内环需要两个PI调节器，控制较为复杂，且PI参数不易整定。文献［2］利用数学推导消除了虚拟输入电流，一定程度简化了控制系统，但电流内环仍有两个PI调节器。本文以单相三电平中点箝位（Neutral Point Clamped，NPC）PWM 整流器为研究对象，提出了基于dq坐标系的电流解耦控制策略。该控制策略消除了有功电流与无功电流的相互影响，并使电流内环控制不依赖于PI控制器，能够实现网侧输入电流正弦化并使系统具有高功率因数。

1 单相三电平NPC PWM整流器

单相三电平NPC PWM整流器的主电路如图1所示，它由8个IGBT模块构成两组对称的桥臂，每组桥臂各有两个箝位二极管，C1、C2分别为两个直流侧支撑电容，Ls、Rs分别为变压器二次侧漏感和漏电阻。为便于分析，忽略漏电阻Rs，定义开关函数如下：

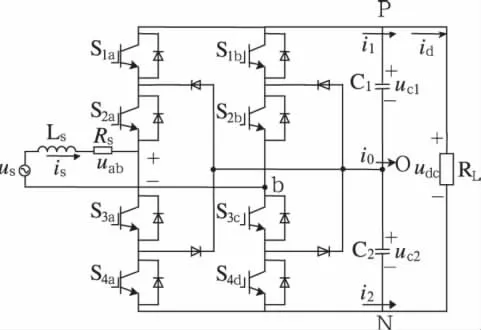
图1 单相三电平NPC整流器

由式（1）、（2）可以看出SA和SB均具有三种工作状态。以a桥臂为例，当开关函数SA＝1、0、－1时，uao分别对应udc/2、0、－udc/2。因此，单相三电平 NPC整流器具有3×3＝9个工作模式。输入端电压uab如图2所示，由单相三电平NPC整流器的9个工作模式可知uab有5个台阶，每个台阶对应一个或多个工作模式。

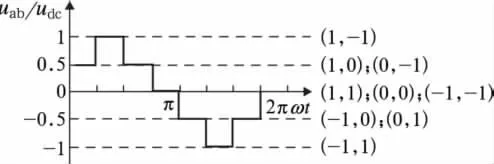
图2 输入端电压uab与工作模式对应关系示意图

假设开关为理想器件，且换相过程中无能量损失，则单相三电平NPC整流器交流侧与直流侧瞬时功率相等。对图1中主电路的交流侧回路采用KVL可得：

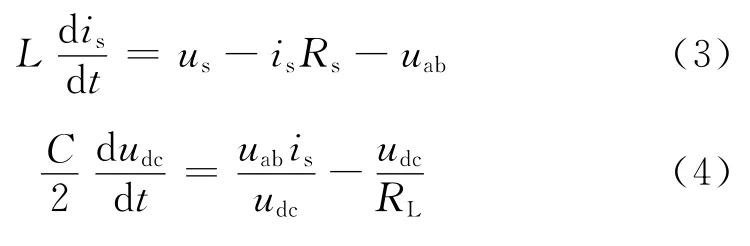
2 控制策略

PWM整流器一般采用电压外环、电流内环的双闭环控制策略［4］。图3所示为PWM整流器的双闭环控制框图，参考电压与直流输出电压udc比较的误差信号送入PI调节器，其输出作为参考电流的幅值。通过锁相环（PLL）检测输入电压us获得参考电流的频率和相位，从而保证了和us同频同相位。因此，电流内环控制的目的是要保证输入电流is能够很好地跟踪参考电流，从而实现网侧输入端的单位功率因数。

图3 PWM整流器双闭环控制框图

2.1 变量定义

单相PWM整流器中，网侧输入电压us、输入电流is和整流器输入端电压uab可分别定义为［2］：

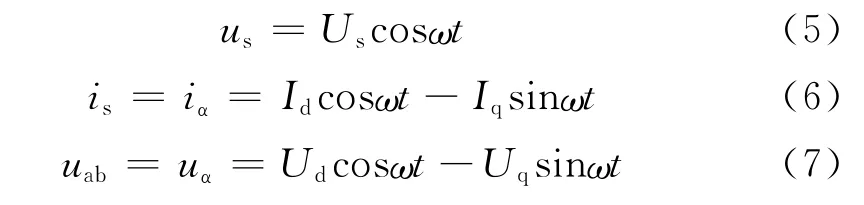
式中：Id、Iq分别为输入电流的有功、无功分量的幅值；Ud、Uq分别为整流器输入端电压d轴、q轴分量的幅值。由于单相系统中只有一个输入电流变量，dq变换不能直接应用［2］。为了解决这个问题，需引入一个虚拟输入电流变量iβ。如前所述，参考电流的频率和相位通过锁相环（PLL）检测输入电压us获得，将定义为，同时假设β轴上的电流参考分量与同频率，且滞后其π/2，可得：

由式（6）可知，网侧输入电流is分解为d轴上的有功分量和q轴上的无功分量。显然，PWM整流器的控制目标是使无功分量为0。再将式（8）、（9）进行坐标变换可得输入电流有功分量的参考值，即：

2.2 整流器数学模型

将式（6）和（7）代入式（3），令等式中正弦项系数和余弦项系数分别相等，则可推导出基于dq坐标系单相三电平NPC PWM整流器的平均值数学模型为：

由式（12）可知，PWM整流器中有三个状态变量Id、Iq、udc，两个输入变量Ud、Uq，通过控制Ud、Uq来控制Id。但在状态方程中Id、Iq并不独立，彼此之间存在耦合关系，因此传统的线性控制方法很难达到理想的控制性能。

2.3 电流解耦控制策略

为了提高单相三电平NPC PWM整流器电流内环的控制性能，简化控制系统设计，电流内环采用线性解耦控制。其控制思想是：引入新的输入变量、，通过两个独立输入变量使得Id、Iq转化为解耦的线性关系。则新的输入变量、与状态变量之间的关系可描述为：

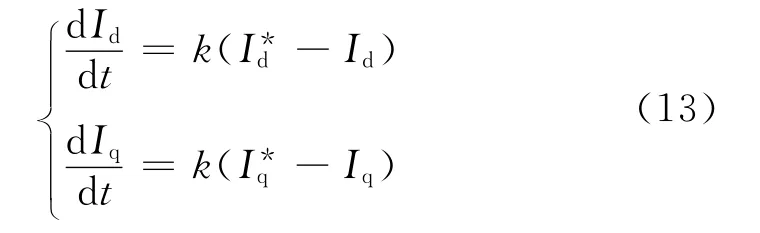
将式（13）代入（12）可得：

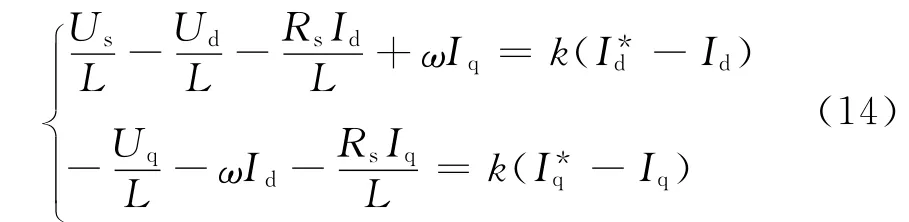
忽略Rs大小，由上式可得：

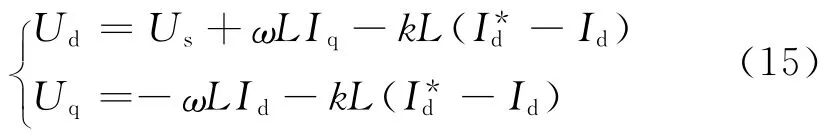
图4 电流解耦控制框图

由图4可知，引入比例系数k后，电流内环中的PI调节器换成了比例调节器，一定程度上降低了控制系统的复杂度。此外，电网电压幅值Us需作为前馈补偿量用来消除网压波动对系统的影响。

2.4 SVPWM 调制

根据调制信号um的大小可将单相三电平NPC整流器的9个工作模式划分为如下4个工作区域：

（1）区域1：0.5＜um/udc＊≤1；

（2）区域2：0＜um/udc＊≤0.5；

（3）区域3：－0.5＜um/udc＊≤0；

（4）区域4：－1≤um/udc＊≤－0.5。

其中udc＊为直流参考电压。

单相三电平NPC整流器9个工作状态对应9个空间电压矢量，其中3个零矢量VPP、VOO、VNN，4个小矢量VPO、VON、VNO、VOP，和2个大矢量VPN、VNP。矢量VXY中，X 表示SA的值（P、O、N），Y 表示SB的值（P、O、N）。图5为SVPWM调制方式，调制信号um由幅值相差/2的两个状态量V1和V2的线性组合来合成［5］。在每个区域V2从大矢量或零矢量中选择，而V1有两个冗余状态量V1＋和V1－，且冗余状态量只从小矢量中选择［6］。

图5 SVPWM调制

由图5可以看出V1和V2满足下式：

在一个开关周期Ts内，调制信号um可视为恒定值，利用伏秒平衡原理可得：

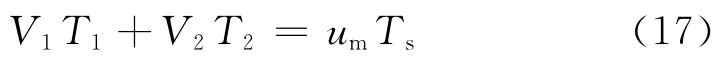
T1与T2分别为V1和V2的作用时间，且满足：

联立式（17）、（18）可得：

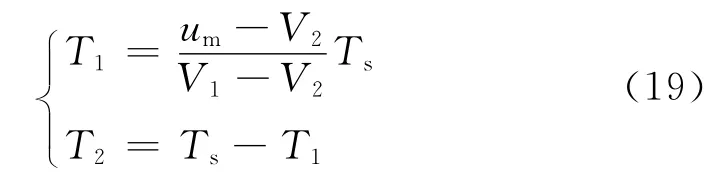
表1给出了4个工作区域中状态量V1、V2与9个空间电压矢量之间对应的矢量关系。

表1 状态量与空间电压矢量在4个工作区域中对应关系

为减小开关损耗和开关应力，文献［7］提出优化的状态量作用顺序，分别为状态量作用顺序I：V1＋→V2→V1－→V2→V1＋和状态量作用顺序II：V1－→V2→V1＋→V2→V1－，对应状态量的作用时间分别为：T1＋/2→T2/2→ T1－→T2/2→T1＋/2 和 T1－/2→T2/2→T1＋→T2/2→T1－/2。

3 仿真和实验结果

为验证电流解耦控制策略的可行性，采用PSIM进行计算机仿真，并进行了相应的样机测试。系统参数如下：输入电压有效值实验us＝ 50 V，Ls＝4.3 mH，Rs＝0.2Ω，开关频率fs＝2.5 kHz，直流参考电压100 V，支撑电容C1＝C2＝3 300μF，负载功率200 W。

图6为输入电流无功分量参考值等于零时，1/2负载向满载切换（1 s）前后的仿真波形，其中（a）为输入电流有功无功分量幅值及其给定值波形；（b）为网侧输入电压电流波形；（c）为输出直流电压。由图6（a）可知，无论系统1/2负载还是满载运行，输入电流的有功、无功分量都能够很好地跟踪其给定值。由图6（b）可知，网侧输入电流正弦度好，且能够很好地跟踪输入电压，功率因数接近1。由图6（a）、6（c）可知，1 s投入负载后，大约经过0.3 s系统重新进入稳态，且输入电流无功分量一直为零，系统动态性能良好。

图6 1/2负载向满载切换前后系统仿真波形

图7为网侧输入电压电流稳态仿真波形，其中（a）为输入电流无功分量参考值＝1时的波形；（b）为输入电流无功分量参考值＝－1时的波形。由图7（a）可知，当输入电流无功分量参考值＝1时，网侧输入电流超前网侧输入电压，此时整个PWM整流器相对于电网可以等效为一个容性负载，而当输入电流无功分量参考值＝－1时，PWM整流器相对于电网可以等效为一个感性负载。

试验样机与仿真参数一致，功率开关器件采用2MB175U4A－120绝缘栅双极晶体管，驱动电路由具有短路保护功能的PC929搭建而成；采用TMS320F2812数字信号处理器完成系统的采样和电平作用时间计算。

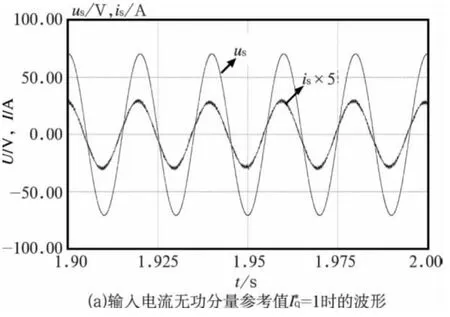
图7 网侧输入电压电流稳态仿真波形

图8为整流工况下网侧输入电压电流实验波形。由图8可知，输入电流is能够很好地跟踪输入电压us，相位与其基本一致，功率因数较高。图9为整流器输入端电压实验波形。

图8 网侧输入电压电流波形

图9 整流器输入端电压波形

4 结 论

本文基于dq坐标系推导了单相三电平NPC PWM整流器的数学模型，提出了电流解耦控制策略。该控制策略不仅实现d、q轴电流的解耦，而且比例控制器的使用大大降低了控制系统设计的复杂性。仿真和实验结果表明：电流解耦控制策略能够消除网侧输入电流的稳态误差，实现网侧高功率因数，并且具有很好的动态特性。

［1］ 一种新的PWM整流器电流解耦控制策略［J］.电工技术学报，2005，20（8）：74－77.

［2］ Miranda U A，Rolim L G B，Aredes M.A DQ Synchronous Reference Frame Current Control for Single－Phase Converters［C］.Power Electronics Specialists Conference，PESC＇2005.IEEE36th 2005：1377－1381.

［3］ Salaet J，Alepuz S，Gilabert A，Bordonau J，Peracaula J.D－Q Modeling and Control of a Single Phase Voltage Balancing［C］.IEEE Power Electronics Specialists Conference，2002，2：514－519.

［4］ 顾 军.基于电流解耦的双闭环三电平PWM整流器研究［J］.电力电子技术，2007，41（6）：60－62.

［5］ Salaet J，Gilabert A，Bordonau J，Alepuz S，Cano and Gimeno，Gimeno LM.Nonlinear Control Neutral Point in Three－level Single－phase Converter by Means of Switching Redundant States［C］.Electronics Letters，2006.

［6］ 冯晓云，宋文胜.单相三电平NPC整流器的SVPWM与中点电位控制方法［J］.西南交通大学学报，2009，44（3）：347－353.