单相LCL并网逆变器双电流闭环控制仿真研究

王 东，薛士龙，宗艳玲

（上海海事大学 物流工程学院，上海201306）

0 引 言

进入21世纪，开发新能源和发展可再生能源，实现经济可持续发展，已成为人类社会的共识。逆变器是光伏系统的核心，同时也是其它新能源如风能开发技术的关键所在，因此研究逆变器的并网控制具有重大意义和重要的应用前景。入网电流的总谐波失真（total harmonic distortion，THD）和并网发电功率因数（power factor，PF）是衡量并网发电电能质量的2项重要指标。因此，常用滤波器来滤除并网逆变器输出中包含的高频PWM谐波，以满足谐波标准［2］。

目前，太阳能发电逐渐向大功率方向发展，风能发电更是出现了兆瓦级以上的容量，采用较低的开关频率，传统的L滤波已经不能满足要求，很多专家学者提出了LCL滤波技术。LCL滤波器对高频分量呈高阻抗特性，对高频谐波电流可起到很大的衰减作用［3］，选取较小的电感值就能实现较好的滤波效果，且系统动态性能好［3］。

但是LCL滤波器是一个三阶系统，易引起输出振荡；对并网逆变器电流控制的设计有更高要求。本文采用并网电流和电容电流双闭环的控制策略，既可减少谐振，又能保证高的并网电流功率因数。

1 滤波器参数设计

采用LCL滤波器的单相光伏并网逆变器主电路结构如图1所示，其中Ud为直流侧输入电压，S1－S4为IGBT功率开关管，Ui（s）为未经滤波的逆变器输出电压，i1为逆变器输出电流，ic为电容支路电流，i2为并网电流，逆变桥采用单极性SPWM技术进行控制。当开关频率远高于输出滤波器的截止频率时，逆变桥可等效为比例环节KPWM。忽略滤波电感的电阻和电容的寄生电阻。

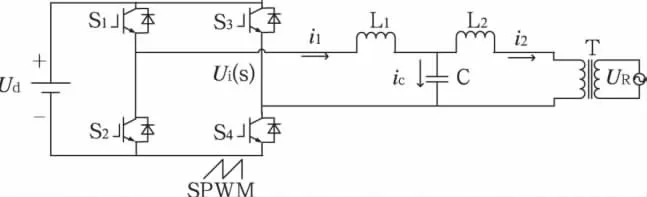
图1 单相LCL并网逆变器主电路

本文先建立一个3 kW/220 V的单相并网逆变器模型。开关频率设定为16 kHz，直流侧电压取为350 V，输出频率为50 Hz，根据电流纹波计算L1＋L2，在低频时LCL滤波器可简化成电感值L为的单电感滤波器，故可用单电感L近似计算L1＋L2的值［4］。

式中，D（t）为占空比，fc为开关频率。由于开关频率远大于工频频率，可得：

代入数值可得：

实际取L＝2.4 mH，不同文献对L2/L1取值不同，本文选择L1＝2 mH，L2＝0.4 mH。

电容参数受系统容量的限制。电容值的增加会降低系统的功率因数，通常在选择电容参数时，电容参数对系统功率容量的影响要小于10%。本文取为5%。

代入数值得：C＝9.87μF，本文取C＝10μF。

2 电流双闭环控制

2.1 控制方案分析

如果对LCL并网逆变器采用并网电流直接控制，其控制框图如图2所示。

图2 i2直接闭环控制框图

由图2可得并网电流i2与PI控制器输出I（s）的传递函数为：

代入参数可得：

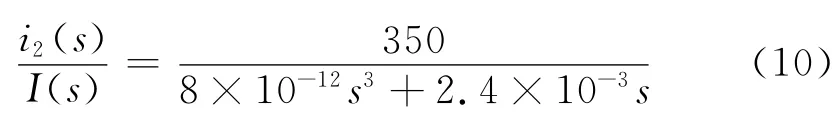
加入电容电流闭环控制，系统结构框图如图3所示：

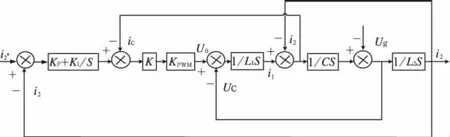
图3 并网电流和电容电流双闭环控制系统结构框图

由图3可得并网电流i2与PI控制器输出I（s）的传递函数为：

令K＝1，代入参数可得到：

分别画出式（10）和式（12）的幅频特性曲线，如图4所示。

图4 幅频特性曲线

由图4可以很明显看出，加入了电容电流内环控制后，谐振尖峰得到了很好的抑制。可见，采用电容电流内环可以增加系统阻尼，从而抑制谐振尖峰，增强系统稳定性。

2.2 控制参数计算

由图3可以得到电容电流内环的传递函数为：

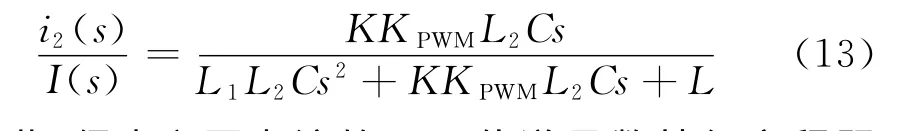
由此，得出入网电流的开环传递函数特征方程阻尼系数为：

工程中通常为了兼顾系统的阻尼和动态特性，一般取ζ＝0.707。将L1，L2，C，KPWM的值代入上式可得到k＝0.14。

本文中外环控制采用PI控制器，PI控制器的参数工程整定法比较多，本文采用振荡指标法。

文献［6］中详细介绍分析了这种PI参数整定方法。本文根据文献［6］中的方法计算得到PI的参数为：KP＝0.5，Ki＝1 200。

由于电网电压并不是固定不变的，所以为了克服电网电压扰动对LCL滤波器的影响，增加了电网电压的前馈环节，根据文献［6］的方法，设定了电网电压前馈函数Gn＝1/KPWM。这样可大大减小电网电压变化对入网电流的干扰。

3 系统仿真分析

为了验证理论分析的正确性和电流双闭环控制系统的稳定性及动态性能，在 Matlab R2008/Simulink仿真环境下进行了仿真。根据前面算出的系统参数，搭建的仿真模型如图5。

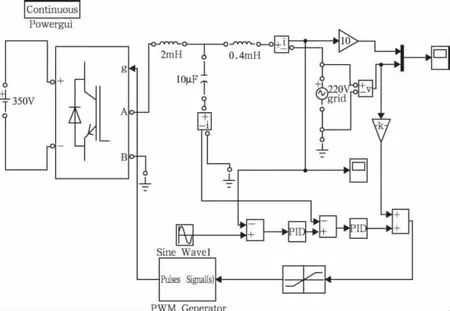
图5 逆变器电流双闭环控制仿真模型

仿真中，输入电压为350 V，开关频率设定为16 kHz，SPWM调制比设定为0.8，参考电流为逆变器额定输出电流19.3 A，图6为电网电压与并网电流放大10倍的波形。

图6 电网电压与并网电流仿真波形

由图6可以看出，使用双闭环电流控制能控制输出电流跟踪电网电压，实现了输出电流和电网电压的同频同相，接近单位功率因数并网。从仿真波形还可以看出，通过滤波器滤波的并网电流谐波含量显著减小，LCL滤波器的效果很好。图7对并网电流前五个周期的仿真波形进行傅立叶分析，THD＝0.69%，仿真效果比较好。

图7 并网电流的FFT分析

为了观察系统的动态响应特性，对逆变器由满载到半载的突变进行动态仿真，其仿真波形如图8所示。

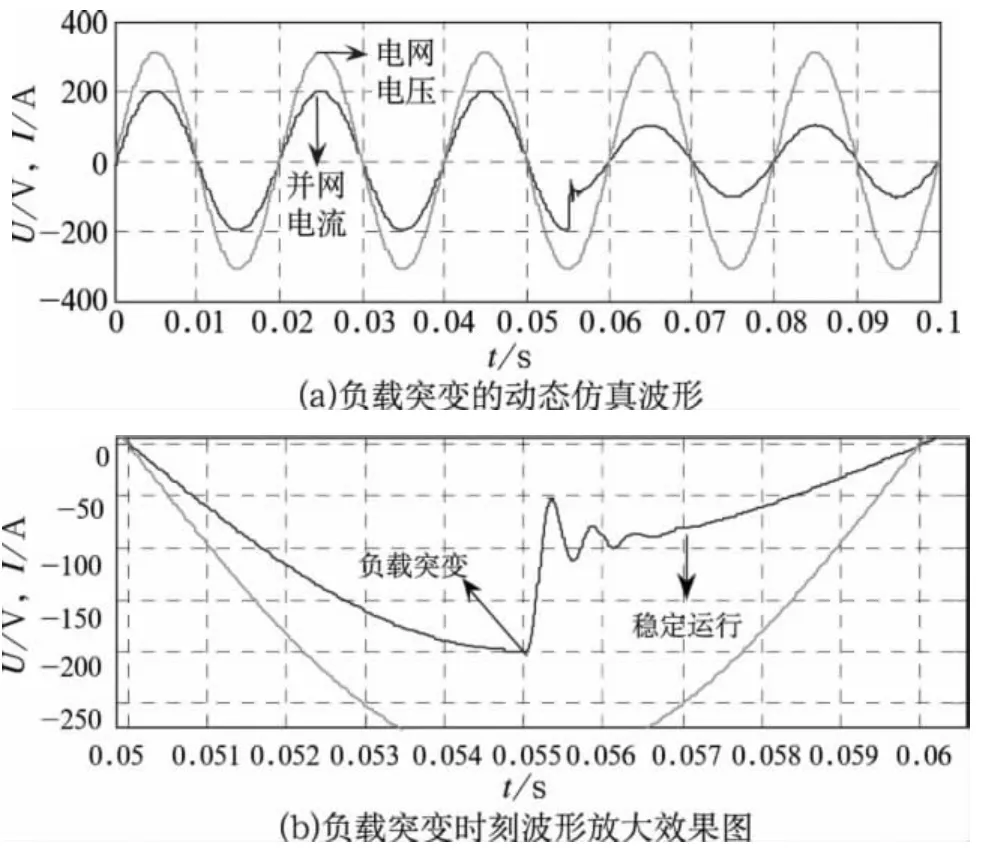
图8 逆变器工作从满载到半载的动态仿真波形

图8（a）中的波形显示了逆变器正常工作时，负载发生突变后，系统能够恢复稳定运行；图8（b）的放大波形显示：在0.055 s时刻负载发生突变，0.057 s时刻逆变器在半载情况下稳定运行。系统在负载突变时的过渡时间为0.002 s，为0.1个周期的时间，可见系统具有较好的稳定性。

4 结 论

LCL滤波器是一个三阶振荡系统，采用并网电流直接闭环控制存在谐振尖峰，易造成系统的不稳定。本文采用了并网电流和电容电流的双闭环控制，加入电网电压前馈控制的控制策略。通过3 kW逆变器的设计和仿真验证，该控制策略可以有效地抑制谐振，提高系统稳定性，系统具有优良的动静态性能。仿真结果还表明并网电流的谐波总量小于5%，达到并网电流标准要求。因此，电流双闭环控制方案是可行的。

［1］ 郑诗程.光伏发电系统及其控制的研究［D］.合肥：合肥工业大学，2004.

［2］ 吴卫民，刘松培，何远彬，耿 攀.单相LCL并网逆变器电流控制综述［J］.电源学报，2011，3：51－57.

［3］ 刘 飞，徐鹏威，陈国强，等.基于LCL滤波器的三相光伏并网控制系统研究［J］.太阳能学报，2008，29（8）：965－970.

［4］ 张 涛.单相LCL滤波器的并网逆变器控制的研究［D］.秦皇岛：燕山大学，2010.

［5］ 王章权.瞬时电流跟踪控制光伏并网技术［J］.电源技术，2007，20（8）：648－650.

［6］ 徐志英.并网逆变器电流控制技术的研究［D］.南京：南京航空航天大学，2009.