GPS非差相位精密单点定位算法研究①

琚兴华

（河南省有色金属地质矿产局第一地质大队，河南 郑州450016）

0 引 言

1997年美国喷气推进实验室（JPL）的Zumbeger等人提出了非差精密单点定位方法。该技术一经提出，便得到许多GPS专业领域学者的重视。这项技术的出现，大大减少了野外作业的劳动强度，降低了作业成本。精密单点定位就是在已知精密星历和卫星钟差的前提下，充分考虑各种误差改正，利用单测站确定其在 WGS－84（或ITRF）坐标系内的坐标［1]。该方法采用的精密星历和卫星钟改正数是由国际地球动力学服务机构（IGS）所提供的，其精密星历的精度已优于5cm，卫星钟改正数的精度已达0.1～0.2ns［2].随着接收机性能的不断改善，载波相位测量的精度也在不断的提高；大气延迟改正模型和改正方法的研究也在不断的深入，这些都为精密单点定位技术奠定了基础。

目前应用较多的GPS非差相位精密单点定位的最小二乘估计法适合于静态方式，不能很好地描述系统的动态特征，而Kalman滤波借助系统的状态转移方程，根据前一时刻的状态估值和当前时刻的观测值，递推估计新的状态估值，更加准确地反映了系统的运动状态［3]。

分别建立了非差动态精密单点定位的标准卡尔曼滤波和附加模糊度参数的卡尔曼滤波，分析了在给定不同初始方差的情况下，对滤波收敛情况的影响，以及在不同采样率的情况下，滤波的计算精度，结果表明：高采样率数据的定位精度高于低采样率数据的定位精度。

1 GPS非差精密单点定位的卡尔曼滤波模型［4－11]

卡尔曼滤波技术是一种处理动态定位数据的有效手段，它可以显著地改善动态定位精度。因为它在定位中不仅利用观测历元的观测值，而且充分利用以前的观测数据，根据线性最小方差原理，求出最优估计，因此，卡尔曼滤波技术在GPS动态定位中获得较为广泛的应用。

1.1 标准卡尔曼滤波模型

研究动态定位的最优滤波问题时，首先要建立比较准确、合理的运动模型。目前已有多种运动模型。在现实当中，常常无法用精确的数学模型来描述一个物体的运动模型，对GPS非差相位动态精密单点定位而言，最常用的动态模型为常速模型或常加速模型。非差精密单点定位的标准卡尔曼滤波模型为

式中：k为观测历元时刻；Xk为n维状态向量；Φk＋1，k为n×n维的一步状态转移矩阵；Γk为n×p维动态噪声矩阵；wk为p维系统动态噪声向量；｛wk｝为零均值白噪声序列，即：E｛wk｝＝0，E｛wk·wT1｝＝Qkδkl，其中Qk为一已知的非负矩阵，δkl为克罗尼克δ函数；Lk＋1表示为m维观测向量；Hk＋1表示为m×n观测矩阵；vk＋1为m维观测噪声向量，｛vk｝为系统动态噪声；｛wk｝为不相关的零均值白噪声序列，即：E｛vk｝＝0，E｛vk·vTl｝＝Rkδkl，E｛wk·vTk｝＝0，其中Rk为一已知的正定阵。

由于标准的卡尔曼滤波方程，除要求动态噪声与观测噪声是零均值、不相关的白噪声序列之外，还要求系统的状态方程与观测方程都是线性的，但在非差相位精密单点定位过程中，系统的物理模型有时需要非线性方程来描述，若要采用标准的卡尔曼滤波方法来估计系统的状态，就需要对非线性的观测方程进行处理。

1.2 附加模糊度参数的滤波模型

当初始相位模糊度已知时，采用简化的标准卡尔曼滤波模型进行滤波处理即可得到较高精度的滤波结果。在大多数情况下，初始相位模糊度是未知数，在这种情况下，将整周模糊度作为状态向量的一部分，与测站坐标、测站速度、接收机钟差及钟差变化率同时估计，称之为附加模糊度参数的滤波模型。伪距观测值作为辅助观测量，和相位观测值一起作为观测值进行估计。

附加模糊度参数的滤波模型的状态向量为

其状态向量的维数变为n＋8，除了估计载体的位置、速度、接收机钟差、钟差变化量8个参数外，还要计算n颗卫星的初始模糊度值。

模糊度的初始值N0／0是利用伪距法求得的。伪距法是在进行载波相位测量的同时又进行了伪距测量，将伪距观测值减去载波相位测量的实际观测值（化为以距离为单位）后即可得到。

2 实验分析

2.1 滤波特性的分析

利用编写的非差精密单点定位程序对2005年7月19日PMOB站的数据进行计算分析。图1和图2描述了依据经验值，当滤波量测噪声矩阵RK＝10，动态噪声矩阵Qk－1＝0.01选定后初始协方差阵的选取对滤波结果的影响。图1中（a）、（c）、（d）示出了将状态向量的初始方差矩阵赋较大值的结果，图1中（b）、（d）、（f）示出了将状态向量的初始方差赋较小值的滤波结果。从两图中可以看出，图中1（a）、（c）、（e）图像在三个坐标轴上的收敛速度都比图1中（b）、（d）、（f）的图像收敛的快，至于滤波稳定后的精度，从图2中可以看出，定位的精度和初始方差的确定没有关系，两者精度几乎一样。在实际计算中，也可以按照经验值确定初始的方差矩阵，状态向量的方差矩阵选择大一些，可使滤波较快地收敛，达到较好的结果。

2.2 伪距非差定位结果分析

利用2005年7月19日PMOB站1s数据和30s数据对伪距进行非差单点定位计算，滤波经过一段时间的初始化后，定位结果如图3所示。图3中（a）、（c）、（e）示出了1s采样率的计算结果；图3中（b）、（d）、（f）示出了30s采样率的计算结果。表1给出了两种采样率数据的伪距定位结果分别在X轴、Y轴和Z轴的平均点位误差。表2、表3、表4对两种采样率数据的伪距定位结果分别在X轴、Y轴和Z轴的点位误差进行了统计，从统计结果可以看出，大部分定位精度在1m以内。

从表1中可以看出，1s采样率的数据计算结果比30s采样率的数据计算结果精度好一些，但两者精度都较低，且差值变化抖动较大，最大位置误差达2.4m.主要是因为伪距本身的精度较载波相位的差，同时受到卫星观测几何图形和低高度角卫星观测值的影响，因此，其定位精度只能达到米级，不能满足高精度定位的要求。但是在非差定位中，利用伪距观测值可以确定非差相位整周模糊度的初始值，因此它是必需的，并且质量越高对模糊度的快速确定越有利。

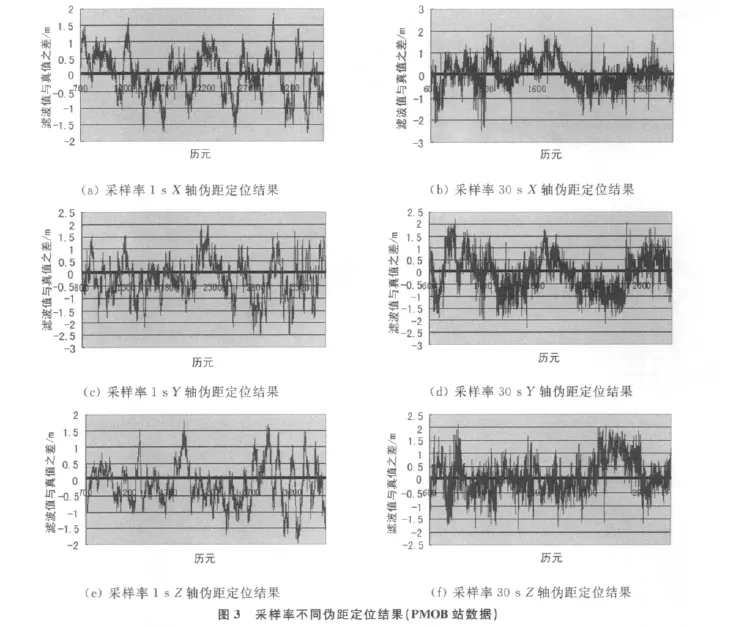
表1 伪距平均点位误差比较

表2 X轴伪距平均点位误差统计

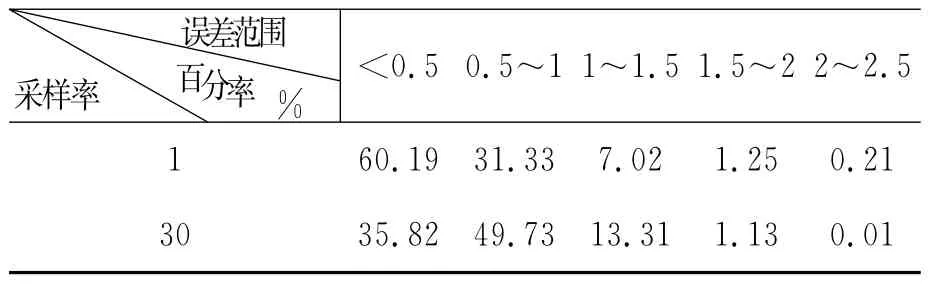
表3 Y轴伪距平均点位误差统计

表4 Z轴伪距平均点位误差统计

2.3 载波相位非差定位结果分析

使用同样的数据，利用附加模糊度参数的卡尔曼滤波对载波进行非差精密单点定位计算，滤波结果如图4所示，图4中（a）、（c）、（e）示出了1s采样率的计算结果，图4中（b）、（d）、（f）示出了30s采样率的计算结果。在计算过程中，采用15阶切比雪夫多项式拟合卫星轨道坐标和卫星钟差，初始整周模糊度采用双频伪距粗略计算得到。为了能够更快地确定整周模糊度，仍然将伪距作为辅助观测值参与处理，只是将非差相位观测值赋予较高的权，伪距观测值赋予较低的权。经过一段时间的初始化后，计算结果和已知坐标值进行比较。

图4中，（a）、（c）、（e）示出了在1h内可见卫星数目固定为8颗的情况下得到的计算结果，图4中（b）、（d）、（f）示出了全天24h内卫星数目变化的情况下的结果。当卫星数目变化时，把状态变量中新出现的卫星所对应的模糊度赋初值，重新滤波。

表5 载波定位平均点位误差统计

表6 X轴载波定位平均点位误差统计

表7 Y轴载波定位平均点位误差统计

表8 Z轴载波定位平均点位误差统计

表5列出了两种采样率数据的载波定位结果分别在X轴、Y轴和Z轴的平均点位误差。表6、表7、表8对两种采样率数据的载波定位结果分别在X轴、Y轴和Z轴的点位误差进行了统计。从统计结果可以看出载波定位的结果大部分在0.5 m以内，对于1s采样率数据定位效果明显好于30 s采样率数据。从表5中可以看出，附加模糊度参数的卡尔曼滤波定位精度较高，1s采样率的计算结果精度一般都在1m以内，相比之下30s采样率的精度没有前者高。究其原因主要是因为当卫星在升降过程中，卫星数目变化导致滤波的部分状态变量需要赋初值，这需要一个稳定的过程，而在稳定期间，其观测数据又偏少，所以30s采样率的计算结果精度不如1s采样率的精度。

3 结 论

非差精密单点定位是GPS发展的热点问题，研究了GPS非差精密单点定位的算法以及Kalman滤波在该模型中的应用，建立了非差精密单点定位的标准卡尔曼滤波和附加模糊度参数的卡尔曼滤波，通过算例验证了算法的可靠性和实用性。分析了不同采样率情况下，滤波的计算精度，结果表明：1s采样率的定位精度相对较高。

［1]李征航，吴秀娟.全球定位系统（GPS）技术的最新进展：第四讲精密单点定位（上）［J].测绘信息与工程，2002，27（5）：34－37.

［2]刘红新，程鹏飞，王解先，等.GPS卫星轨道数值积分与广播星历及IGS精密星历的比较［J].测绘科学，2006（4）：42－45.

［3]蔡艳辉，程鹏飞，李夕银.用卡尔曼滤波进行GPS动态定位［J].测绘通报，2006（7）：6－8.

［4]程鹏飞，蔡艳辉，王 华.广域差分的全矢量法［J].测绘工程，2005（9）：1－3.

［5]程鹏飞.建立中国差分GPS服务的研究［J].测绘学报，1999 28（1）：19－21.

［6]周忠谟，易杰军，周 琪.GPS卫星测量原理与应用［M].北京：测绘出版社，1997.

［7]叶世榕.GPS非差相位精密单点定位理论与实现［D].武汉：武汉大学测绘学院，2002.

［8]党亚民，秘金钟，成英燕.全球导航卫星系统原理与应用［M].北京：测绘出版社，2007.

［9]ZUMBERGE J，HEFLIN M，JEFFERSUN D C，et al.Precise point positioning for the efficient and robust analysis of GPS data from large networks［J].Journal of Geophysical Research，1997，102（B3）：5005－5017.

［10]KOUBA J，HEROUX P.Precise point positioning using IGS orbit and clock products［J].GPS Solutions，2001，5（2）：12－28.

［11]祁 芳.卡尔曼滤波算法在GPS非差相位精密单点定位中的应用研究［D].武汉：武汉大学，2003.